SimpleCG绘图函数(9)--绘制各种线条
一、所有线段函数概述
可填充图形绘制函数都介绍完了,还有一些特殊线条的绘制将在本篇进行讲解。所有特殊线条函数如下所示,其中还有一个区域填充函数floodfill比较特殊,是配合线条函数使用的:
//绘制一系列折线段
//折线段以一组POINT表示的点坐标数组ptPoints为端点,nNum表示数组中的点数量
void polyline( const POINT *ptPoints, int nNum );
//绘制一系列贝塞尔曲线
//数组中开始四个点表示贝塞尔曲线起点,控制点1,控制点2,终点
//其中终点将作为下一段塞尔曲线起点,然后是第二段控制点1,控制点2,终点,循环下去
//所以nNum最少有四个点,总共有3*n+1个点
void polybezier( const POINT *ptPoints, int nNum );
//绘制一条曲线,nLength指定拉伸曲度
//绘制一条起点(nStartX, nStartY),到终点(nEndX, nEndY)的曲线,nLength越大曲线越弯曲
void curveline( int nStartX, int nStartY, int nEndX, int nEndY, int nLength );
//绘制一系列曲线
//一系列曲线以一组POINT表示的点坐标数组ptPoints为端点,nNum表示数组中的点数量以及曲度pLength的元素数量,pLength的数量为nNum-1。
void polycurvelinevar( const POINT *ptPoints, int *pLength, int nNum );
//画椭圆弧
//椭圆弧所在椭圆的外切矩形左上角坐标(left, top),右下角坐标(right, bottom),起始角度stangle,终止角度endangle,角度采用弧度表示,也就是单位圆的弧长度
void arc( int left, int top, int right, int bottom, double stangle, double endangle );
//绘制一条波浪线
//绘制一条起点(nStartX, nStartY),到(nEndX, nEndY)波浪线,nLength指定拉伸曲度,nNumLine指定波浪数
void wavyline( int nStartX, int nStartY, int nEndX, int nEndY, int nLength, int nNumLine );
//填充区域
//以点(nStartX, nStartY)为起点,开始填充区域,nFillType=enumFFT_BORDER时,填充nColor边线围成的区域。
//当nFillType=enumFFT_SURFACE时,填充nColor指定的一块颜色
void floodfill( int nStartX, int nStartY, COLORREF nColor, int nFillType );由于线条类型比较多,我们分别进行一一展示。
二、各个线段函数演示
1、首先看polyline
跟多边形绘制差不多,参数一致,不同的是polyline不对图形进行填充,只是绘制系列点连接的线段。看如下代码对比:
setfillcolor(RGB(220,240,255));
POINT pt[]={{20,20},{300,20},{300,150},{20,150}};
fillpolygon(pt,sizeof(pt)/sizeof(pt[0]));
POINT pt1[]={{20,220},{300,220},{300,350},{20,350}};
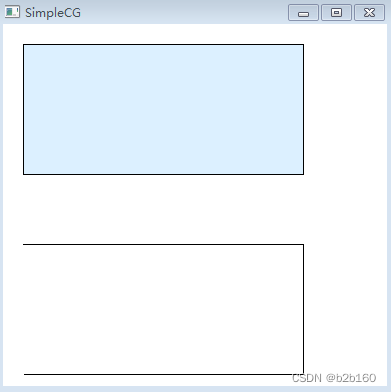
polyline(pt1,sizeof(pt1)/sizeof(pt1[0]));运行效果如图:
polyline只是单纯把数组中的点连接起来,并不会自动封闭图形。
2、然后是绘制系列贝塞尔曲线的函数polybezier
这是一个非常有用的函数,几乎可以拟合任何曲线,所以对于勾画图形非常重要。其中TrueType字体就是使用了贝塞尔曲线进行拟合,文字的笔画何其复杂,可想而知该函数的强大。当然掌握它也有一定难度。
先看看简单的只有两个端点,两个控制点的贝塞尔曲线演示
POINT pt[]={{20,100},{120,0},{200,200},{300,100}};
polybezier(pt,sizeof(pt)/sizeof(pt[0]));点(20,100)到点(300,100)的曲线,控制点分别在(120,0)和(200,200),两端点之间,而且一上一下,曲线如图所示
曲线如同橡皮筋,被拉向两个端点。
所以只要精确控制端点和控制点,就能绘制任意曲线。下面我们尝试利用它来绘制心形。
POINT pt[]={{20,100},{20,20},{150,20},{150,100},//左上半圆
{150,20},{280,20},{280,100},//右上半圆
{280,200},{180,200},{150,300},//右下心
{120,200},{20,200},{20,100}};//左下心
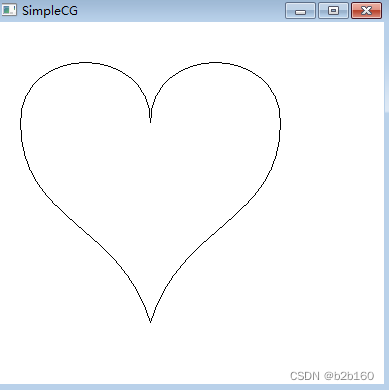
polybezier(pt,sizeof(pt)/sizeof(pt[0]));如图所示
可以看到通过控制点的“拉扯”,很简单就能绘制出优美的符合预期的线条。不过绘制出的线条如果需要填充颜色则需要后面介绍的floodfill函数。
3、下面再看看简单曲线curveline的绘制
贝塞尔曲线需要确定两个控制点,有时一些简单曲线并不需要那么高的自由度,则可以选择curveline来绘制。它可以简单的定义两个端点及一个弯曲程度的参数就绘制出一个弯曲曲线,有时也是比较方便。例如如下代码
curveline(20,100,300,100, 40);就绘制出以下曲线
其中前面四个参数(20,100,300,100)定义了起点和终点,最后一个参数 int nLength,,在此处是40定义了弯曲程度,越大拉伸越厉害,当为正数时表示往终点方向的右侧拉伸,负数则往左拉伸。
4、用多个点绘制一条曲线polycurvelinevar。
上面的函数通过两个点绘制一条简单曲线,而polycurvelinevar则可以同时传入多个点,并以该系列点首尾连接,构成一条复杂的曲线,一系列曲线以一组POINT表示的点坐标数组ptPoints为端点,nNum表示数组中的点数量以及曲度pLength的元素数量,其中pLength的数量为nNum-1。
例如如下代码,用曲线模拟一个近似圆
POINT pt[]={{100,100},{200,100}
,{200,200},{100,200}
,{100,100}};//5个点围成一个正方形
int nLength[] = { -30,-30,-30,-30};//每条边往左边拉伸
polycurvelinevar(pt, nLength, sizeof(pt)/sizeof(pt[0]));运行如图所示
可以看出此函数比贝塞尔曲线更简单操控,只是自由度没那么高,要达到理想状态,需要定义更多的点。
5、再来看看椭圆弧绘制函数arc
函数如下
void arc( int left, int top, int right, int bottom, double stangle, double endangle );
参数说明请参考前面的代码,此函数与polyline类似,它的参数与形状函数扇形是一致的,只不过arc同样也只绘制线段。可通过下面的代码看看它们的区别:
setfillcolor(RGB(220,240,255));
fillpie( 20, 20, 300, 150, 0, -C_PI/3);
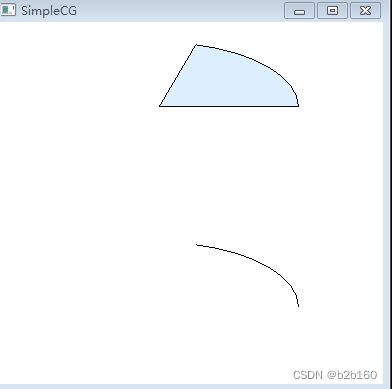
arc( 20, 220, 300, 350, 0, -C_PI/3);绘制效果如图:
这个只绘制圆弧线段在一些情况下作用很大,例如前面绘制的奥运五环,就可以使用这个函数绘制圆圈的环环相扣效果。
6、绘制一条波浪线wavyline
void wavyline( int nStartX, int nStartY, int nEndX, int nEndY, int nLength, int nNumLine );
绘制一条起点(nStartX, nStartY),到(nEndX, nEndY)波浪线,nLength指定拉伸曲度,nNumLine指定波浪数。直接看如下演示代码:
wavyline( 20, 100, 320, 100, 6, 10 );
wavyline( 20, 100+100, 320, 100+100, 6, 20 );两个函数分别用不同的波浪数,同样的曲度,绘制了同样的长度两条波浪线,通过对比可以很容易掌握波浪线的绘制方法。
运行效果如图:
7、区域填充函数floodfill
void floodfill( int nStartX, int nStartY, COLORREF nColor, int nFillType );
需要注意的是有两种填充模式,分别如下:
nFillType=enumFFT_BORDER时,填充nColor边线围成的区域。
nFillType=enumFFT_SURFACE时,填充nColor指定的一块颜色。
可以通过如下代码演示他们的用法。我们先内外绘制大小两个正方形围成的图形。外围正方形我们用波浪线来绘制。
//以下四条波浪线围成一个大正方形
wavyline( 20, 20, 320, 20, 6, 10 );
wavyline( 320, 20, 320, 320, 6, 10 );
wavyline( 320, 320, 20, 320, 6, 10 );
wavyline( 20, 320, 20, 20, 6, 10 );
//绘制一个红色正方形
setlinecolor(RGB(255,0,0));
rectangle( 120,120,220,220);然后分别用两种模式在同一个点进行填充。
setfillcolor(RGB(220,240,255));
floodfill(25, 25, RGB(0,0,0), enumFFT_BORDER );setfillcolor(RGB(220,240,255));
floodfill(25, 25, RGB(255,255,255), enumFFT_SURFACE );原始图形和填充效果如下所示:
我们看到enumFFT_BORDER模式一直填满到遇到黑色边,所以整个大正方形都填满了。而enumFFT_SURFACE模式则只填充指定点周围白色区域,也就是中间的框。
三、总结及综合演示
以上将所有线段函数详细介绍完了,另外还介绍了一个与线段函数配合使用的floodfill函数。通过以上函数几乎可以模拟所有的矢量图形,前提是只要你能熟练掌握它们。与前面几篇介绍的基础图形绘制相比,本篇所述函数可以绘制生活中各种奇异形状,相比规则图形,也许奇异线条构成的图形更加常见,所以本篇内容在绘图中更加实用。下面就以一个哆啦A梦的绘制演示以上函数的运用。
代码如下:
// Curveline.cpp : 定义控制台应用程序的入口点。
//
#include "../import/include/CGBoard.h"
#include "math.h"
#ifdef _DEBUG
#pragma comment(lib,"../import/lib/SimpleCG_MDd.lib")
#else
#pragma comment(lib,"../import/lib/SimpleCG_MD.lib")
#endif
#define ADDCOLOR(x,y) ((x+y)>255?255:(x+y))
#define SUBCOLOR(x,y) ((x-y)<0?0:(x-y))
int g_nWidth = 500; //画面宽度
int g_nHeight= 800; //画面高度
void DrawDora( int nX, int nY )
{
setlinewidth( 4 );
//竹蜻蜓
{
POINT pt[]={ { 300, 35},{ 200, 20 }
,{ 190, 45}
,{ 290, 55}
,{ 300, 35}
};
int nLength[] = { 16, 12, 16, 12 };
polycurvelinevar(pt, nLength, sizeof(pt)/sizeof(pt[0]));
}
curveline(235,30,204,35,4);
curveline(242,37,225,38,2);
curveline(250,47,266,46,2);
curveline(245,55,286,50,4);
setfillcolor(RGB(244,225,122));
fillpie( 240, 40, 250, 140, 0, -C_PI );
fillpie( 225, 90, 265, 127, 0, -C_PI );
//头
{
POINT pt[]={ {235,107}, {264,107}, {325,109}, {367,156}, {409,203}, {398,314}, {376,349}, {354,384}, {350,387}, {340,398}, {330,409}, {161,414}, {125,385}, {89,356}, {57,314}, {66,239}, {75,164}, {151,107}, {237,107} };
polybezier(pt, sizeof(pt)/sizeof(pt[0]));
setfillcolor(RGB(1,144,214));
floodfill(235,117,0,enumFFT_BORDER);
}
//脸
{
POINT pt[]={{237,190}, {266,190}, {321,193}, {348,237}, {375,281}, {362,352}, {343,380}, {324,408}, {232,408}, {214,408}, {196,408}, {160,413}, {124,384}, {88,355}, {68,294}, {79,241}, {90,188}, {176,188}, {237,190} };
polybezier(pt, sizeof(pt)/sizeof(pt[0]));
setfillcolor(RGB(255,255,255));
floodfill(237,200,0,enumFFT_BORDER);
}
//嘴
{
POINT pt[]={{111,268}, {81,246}, {83,264}, {86,275}, {88,300}, {155,281}, {189,276}, {223,271}, {320,266}, {323,282}, {326,298}, {264,384}, {207,385}, {150,386}, {109,293}, {109,290} };
polybezier(pt, sizeof(pt)/sizeof(pt[0]));
setfillcolor(RGB(232,47,37));
floodfill(189,285,0,enumFFT_BORDER);
}
{
POINT pt[]={{306,314}, {278,293}, {192,310}, {162,365}};
int nLength[] = { 5, 12, 8 };
polycurvelinevar(pt, nLength, sizeof(pt)/sizeof(pt[0]));
setfillcolor(RGB(232,65,28));
floodfill(170,350,0,enumFFT_BORDER);
}
//眼睛
setfillcolor(RGB(254,254,254));
fillellipse(130,130,200,220);
fillellipse(200,130,270,220);
setfillcolor(0);
fillellipse(160,187,170,205);
fillellipse(230,190,240,205);
//鼻子
setfillcolor(RGB(239,40,35));
fillcircle(186,230,18);
setfillcolor(RGB(254,254,254));
solidcircle(190,224,6);
//胡子
line(100,220,150,237);
line(90,240,148,250);
line(91,262,147,263);
line(186,247,186,276);
line(300,214,244,231);
line(308,236,250,244);
line(309,260,250,260);
//脚
{
POINT pt[]={{315,568}, {340,564}, {325,563}, {348,564}, {363,571}, {347,639}, {299,639}, {251,639}, {249,603}, {244,575}};
polybezier(pt, sizeof(pt)/sizeof(pt[0]));
}
{
POINT pt[]={{427,472}, {455,468}, {464,502}, {472,519}, {480,536}, {483,598}, {439,606}, {395,614}, {387,591}, {377,570}};
polybezier(pt, sizeof(pt)/sizeof(pt[0]));
}
//身体
{
POINT pt[]={{336,406}, {397,319}, {396,313}, {429,323}, {462,333}, {407,425}, {400,440}, {427,451}, {450,518}, {418,551}, {386,584}, {357,558}, {349,567}, {340,581}, {342,586}, {296,591}, {250,596}, {154,522}, {148,475}, {121,466}, {33,420}, {52,382}, {71,344}, {148,399}, {173,412}, {198,425}, {319,406}, {335,405}};
polybezier(pt, sizeof(pt)/sizeof(pt[0]));
setfillcolor(RGB(1,144,214));
floodfill(336,416,0,enumFFT_BORDER);
}
{
POINT pt[]={{171,417}, {231,409}, {305,415}, {331,432}, {357,449}, {387,527}, {315,555}, {243,583}, {164,533}, {147,468}, {140,448},{151,427},{171,417}};
polybezier(pt, sizeof(pt)/sizeof(pt[0]));
setfillcolor(RGB(254,254,254));
floodfill(181,427,0,enumFFT_BORDER);
}
{
POINT pt[]={{174,481}, {209,484}, {242,499}, {309,473}, {331,487}, {310,548}, {260,545}, {212,542}, {184,529}, {174,481}};
polybezier(pt, sizeof(pt)/sizeof(pt[0]));
}
//铃铛
{
POINT pt[]={{132,392}, {224,408}, {352,382}, {342,403}, {222,426}, {132,408}, {132,392}};
setfillcolor(RGB(232,47,37));
fillpolygon(pt, sizeof(pt)/sizeof(pt[0]));
setfillcolor(RGB(248,216,24));
fillcircle(225,436,25);
setfillcolor(0);
solidcircle(225,446,7);
line(225,446,225,460);
curveline(205, 423,243,423,-4);
curveline(201, 430,247,430,-4);
}
//手
setfillcolor(RGB(254,254,254));
fillcircle(50,372,30);
fillcircle(434,318,30);
//尾巴
{
POINT pt[]={{403,432}, {430,425}, {430,450}, {420,463}};
polybezier(pt, sizeof(pt)/sizeof(pt[0]));
setfillcolor(RGB(232,47,37));
floodfill(413,442,0,enumFFT_BORDER);
}
}
void DrawProcess()
{
DrawDora(20,20);
}
int _tmain(int argc, _TCHAR* argv[])
{
//初始化
if( !ShowingBoard(g_nWidth,g_nHeight, DrawProcess))
return 1;
//关闭图库
CloseBoard();
return 0;
}运行效果如下:
可以看到此例子运用大量曲线绘制方法勾绘线条,用floodfill进行色彩填充.充分展示了线条绘制函数的使用方法。通过对这些函数的学习,一定能让你在电脑绘图上得心应手。