【C++ map、set】

一、什么是AVL树

1.1AVL树的发展背景

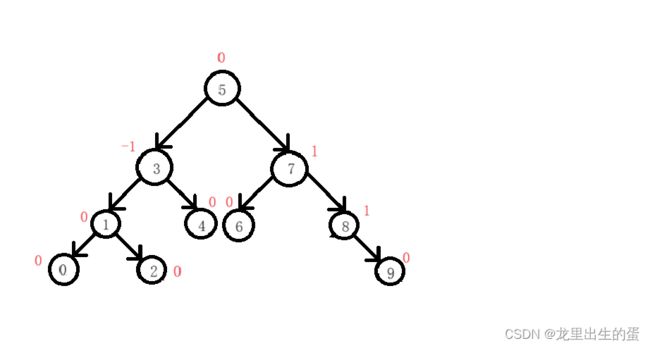
我们都知道搜索树的效率最高的时候就是搜索树最满（满二叉树）的时候。但是现实中的搜索树可能是这个样子。如下图：

那这样的搜索树跟一个查找的效率跟一维数组没什么区别。为了避免出现这样的情况，所以引入了AVL树。

1.2AVL树的概念

发明了一种解决上述问题的方法：当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整)，即可降低树的高度，从而减少平均搜索长度。

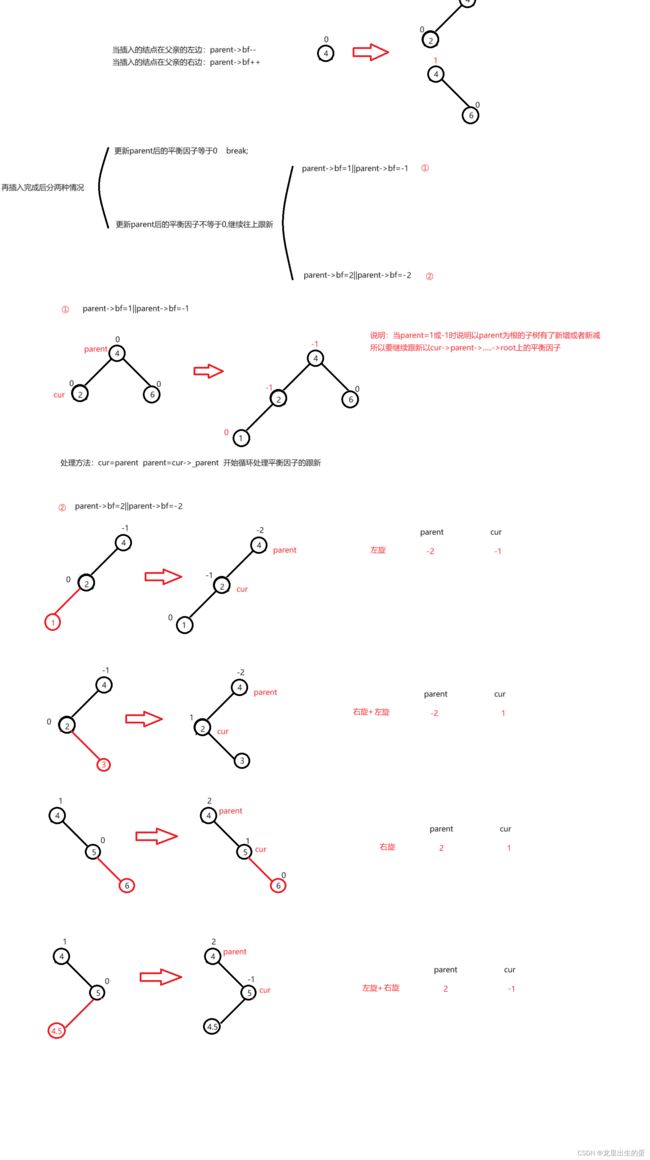
二、AVL树的插入实现

2.1 AVL树实现的框架

为了方便代码的编写，在树的结点中要有平衡因子、左节点、右节点、父亲结点等

template<class K,class V>
struct TreeNode
{
	TreeNode<K, V>* _left;
	TreeNode<K, V>* _right;
	TreeNode<K, V>* _parent;
	pair<K, V> _p;
	int _bf;

	TreeNode(const pair<K, V>& p)
		:_left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _p(p)
		, _bf(0)
	{}
};

template<class K,class V>
class AVLTree
{
	typedef TreeNode<K, V> Node;
public:
	AVLTree()
		:_root(nullptr)
	{}
private:
	Node* _root;
};

2.2AVL树插入的算法思想

旋转的思想

2.3AVL树插入的代码实现

#pragma once
#include
using namespace std;
#include
template<class K,class V>
struct TreeNode
{
	TreeNode<K, V>* _left;
	TreeNode<K, V>* _right;
	TreeNode<K, V>* _parent;
	pair<K, V> _p;
	int _bf;

	TreeNode(const pair<K, V>& p)
		:_left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _p(p)
		, _bf(0)
	{}
};

template<class K,class V>
class AVLTree
{
	typedef TreeNode<K, V> Node;
public:
	AVLTree()
		:_root(nullptr)
	{}
	bool insert(const pair<K, V>& p)
	{
		if (_root == nullptr)
		{
			_root = new Node(p);
			return true;
		}
		Node* cur = _root;
		Node* parent = _root;
		while (cur)
		{
			if (cur->_p.first > p.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (cur->_p.first < p.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				return false;
			}
		}

		cur = new Node(p);
		if (parent->_p.first > p.first)
		{
			parent->_left = cur;
		}
		else
		{
			parent->_right = cur;

		}
		cur->_parent = parent;

		while (parent)
		{
			if (cur == parent->_left)
			{
				parent->_bf--;
			}
			else
			{
				parent->_bf++;
			}
			if (parent->_bf == 0)
			{
				break;
			}
			else if (parent->_bf == 1 || parent->_bf == -1)
			{
				cur = parent;
				parent = cur->_parent;
			}
			else if (parent->_bf == 2 || parent->_bf == -2)
			{
				//旋转
				//斜线且右边高 左旋
				if (parent->_bf == 2 && cur->_bf == 1)
				{
					RotateL(parent);
				}
				//斜线且左边高 右旋
				else if(parent->_bf == -2 && cur->_bf == -1)
				{
					RotateR(parent);
				}
				else if (parent->_bf == 2 && cur->_bf == -1)
				{
					RotateRL(parent);
				}
				else if (parent->_bf == -2 && cur->_bf == 1)
				{
					RotateLR(parent);
				}
				else
				{
					assert(false);
				}

				break;
			}
			else
			{
				assert(false);
			}
		}
		return true;
	}

	int Height(Node* root)
	{
		if (root == nullptr)
		{
			return 0;
		}
		int leftheight = Height(root->_left);
		int rightheight = Height(root->_right);

		return leftheight > rightheight ? leftheight + 1 : rightheight + 1;
	}

	bool isBalance(Node* root)
	{
		if (root == nullptr)
		{
			return true;
		}
		int leftHeight = Height(root->_left);
		int rightHeight = Height(root->_right);
		if (rightHeight - leftHeight != root->_bf)
		{
			return false;
		}
		if (abs(leftHeight - rightHeight) > 2)
		{
			return false;
		}

		return isBalance(root->_left) && isBalance(root->_right);

	}

	bool isBalance()
	{
		return isBalance(_root);
	}
	

private:
	Node* _root;
	void RotateL(Node* parent)
	{
		Node* cur = parent->_right;
		Node* curleft = cur->_left;
		Node* ppnode = parent->_parent;

		parent->_right = curleft;
		if (curleft)
		{
			curleft->_parent = parent;
		}
		cur->_left = parent;
		parent->_parent = cur;

		if (parent == _root)
		{
			_root = cur;
		}
		else
		{
			if (ppnode->_left == parent)
			{
				ppnode->_left = cur;
			}
			else
			{
				ppnode->_right = cur;
			}
		}
		cur->_parent = ppnode;

		parent->_bf = cur->_bf = 0;
	}

	void RotateR(Node* parent)
	{
		Node* cur = parent->_left;
		Node* curRight = cur->_right;
		Node* ppnode = parent->_parent;

		cur->_right = parent;
		parent->_left = curRight;

		if (curRight)
		{
			curRight->_parent = parent;
		}

		parent->_parent = cur;

		if (parent == nullptr)
		{
			_root = cur;
		}
		else
		{
			if (ppnode->_left == parent)
			{
				ppnode->_left = cur;
			}
			else
			{
				ppnode->_right = cur;
			}
			cur->_parent = ppnode;
		}

		parent->_bf = cur->_bf = 0;
	}

	void RotateRL(Node* parent)
	{
		Node* cur = parent->_right;
		Node* curLeft = cur->_left;
		int bf = curLeft->_bf;

		RotateR(parent->_right);
		RotateL(parent);

		if (bf == 0)
		{
			parent->_bf = 0;
			cur->_bf = 0;
			curLeft->_bf = 0;
		}
		else if (bf == 1)
		{
			parent->_bf = -1;
			cur->_bf = 0;
			curLeft->_bf = 0;
		}
		else if (bf == -1)
		{
			cur->_bf = 1;
			parent->_bf = 0;
			curLeft->_bf = 0;
		}
		else
		{
			assert(false);
		}

	}

	void RotateLR(Node* parent)
	{
		Node* cur = parent->_left;
		Node* curRight = cur->_right;
		int bf = curRight->_bf;

		RotateL(parent->_left);
		RotateR(parent);

		if (bf == 0)
		{
			parent->_bf = 0;
			cur->_bf = 0;
			curRight->_bf = 0;
		}
		else if (bf == 1)
		{
			parent->_bf = 0;
			cur->_bf = -1;
			curRight = 0;
		}
		else if (bf == -1)
		{
			parent->_bf = 1;
			cur->_bf = 0;
			curRight = 0;
		}
		else
		{
			assert(false);
		}
	}



}; 

2.4AVL树插入及验证的代码实现

#include"RBTree.h"
#include"AVLTree.h"
#include
int main()
{
	//int arr[] = { 4,2,6,1,3,5,15,7,16,14 };
	//RBTree rb;
	//for (auto e : arr)
	//{
 //		rb.insert(make_pair(e,e));
	//	cout << "insert:" << e << "->" << rb.isBalance() << endl;
	//}

	int arr[] = { 4,2,6,1,3,5,15,7,16,14 };
	AVLTree<int, int> at;
	for (auto e : arr)
	{
		at.insert(make_pair(e, e));
		cout << "insert:" << e << "->" << at.isBalance() << endl;
	}

	随机数测试(RBTree)
	//const int N = 10000;
	//srand((unsigned)time(0));
	//RBTree rb;
	//for (int i = 0; i < N; i++)
	//{
	//	rb.insert(make_pair(rand(), rand()));

	//}
	//cout << rb.isBalance() << endl;


	//随机数测试(AVLTree)
	const int N = 10000;
	srand((unsigned)time(0));
	AVLTree<int, int> at;
	for (int i = 0; i < N; i++)
	{
		at.insert(make_pair(rand(), rand()));

	}
	cout << at.isBalance() << endl;

	return 0;
}

三、什么是红黑树

3.1红黑树的背景

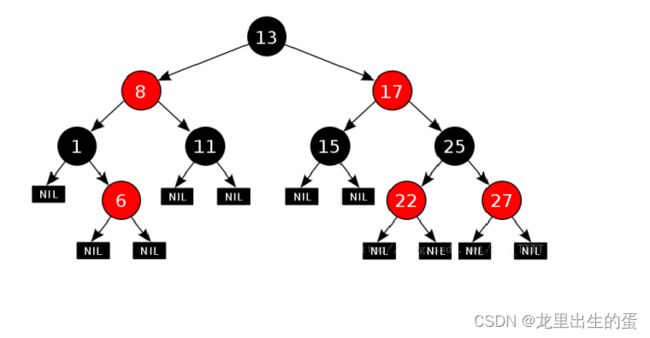
由于上面的AVL树对平衡的机制太过于严格，导致在插入的过程中要多次旋转树的结点，所以引入了这个叫红黑树。如图：

3.2红黑树的性质

1.树的结点颜色不是红色就是黑色
2.如果父亲的颜色是红色，它的儿子只能是黑色
3.最长路径不超过最短路径的二倍
4.根结点是黑色
5.每个路径下的黑色结点数相同

四、红黑树的插入实现

4.1红黑树插入的算法思想

4.2红黑树插入的代码实现

#pragma once
#include
using namespace std;

enum Colour
{
	RED,
	BLACK
};
template<class Key,class Val>
struct RBTreeNode
{
	RBTreeNode<Key, Val>* _left;
	RBTreeNode<Key, Val>* _right;
	RBTreeNode<Key, Val>* _parent;
	pair<Key, Val> _p;
	Colour _col;

	RBTreeNode(const pair<Key, Val>& p)
		:_left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _p(p)
		, _col(RED)
	{}

};

template<class Key,class Val>
class RBTree
{
	typedef RBTreeNode<Key, Val> Node;
public:
	RBTree()
		:_root(nullptr)
	{}

	bool insert(const pair<Key, Val>& p)
	{
		if (_root == nullptr)
		{
			_root = new Node(p);
			_root->_col = BLACK;
			return true;
		}

		Node* parent = _root;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_p.first > p.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				parent = cur;
				cur = cur->_right;
			}
		}

		cur = new Node(p);
		if (parent->_p.first > p.first)
		{
			parent->_left = cur;
		}
		else
		{
			parent->_right = cur;

		}
		parent = cur->_parent;

		while (parent&&parent->_col==RED)
		{
			Node* grandfather = parent->_parent;
			//叔叔在左
			if (parent == grandfather->_left)
			{
				Node* uncle = grandfather->_right;
				//叔叔存在且叔叔为红色
				if (uncle && uncle->_col == RED)
				{
					//变色加向上调整
					parent->_col = BLACK;
					uncle->_col = BLACK;
					grandfather->_col = RED;

					cur = grandfather;
					parent = cur->_parent;
				}
				//叔叔不存在或者叔叔是黑色
				else
				{
					if (cur == parent->_left)
					{
						RotateR(grandfather);
						grandfather->_col = RED;
						parent->_col = BLACK;
					}
					else
					{
						RotateL(parent);
						RotateR(grandfather);
						变色1
						//cur->_col = BLACK;
						//grandfather->_col = RED;
						变色2
						parent->_col = BLACK;
					}
					break;
				}
			}
			else
			{
				Node* uncle = grandfather->_left;
				if (uncle && uncle->_col == RED)
				{
					parent->_col = BLACK;
					uncle->_col = BLACK;
					grandfather->_col = RED;

					cur = grandfather;
					parent = cur->_parent;
				}
				else
				{
					if (cur == parent->_right)
					{
						RotateR(grandfather);

						parent->_col = BLACK;
						grandfather->_col = RED;
					}
					else
					{
						RotateL(parent);
						RotateR(grandfather);

						parent->_col = BLACK;
						grandfather->_col = RED;
					}
					break;
				}
			}
			

		}
		_root->_col = BLACK;
		return true;

	}

	bool isBalance()
	{
		return isBalance(_root);
	}

	bool checkcolour(Node* root, int basevalue,int blacknum)
	{
		if (root == nullptr)
		{
			if (basevalue != blacknum)
			{
				return false;
			}
			return true;
		}
		if (root->_col == RED && root->_parent && root->_col == RED)
		{
			return false;
		}
		if (root->_col == BLACK)
		{
			blacknum++;
		}
		return checkcolour(root->_left, basevalue, blacknum) &&
			   checkcolour(root->_right, basevalue, blacknum);
	}

	bool isBalance(Node* root)
	{
		if (root == nullptr)
		{
			return true;
		}
		if (root->_col != BLACK)
		{
			return false;
		}
		//计算最左路基中黑色结点数量
		int basevalue = 0;
		Node* cur = root;
		while (cur)
		{
			if (cur->_col == BLACK)
			{
				basevalue++;
			}
			cur = cur->_left;
		}

		return checkcolour(root, basevalue,0);
	}
private:
	Node* _root;

	void RotateL(Node* parent)
	{
		Node* cur = parent->_right;
		Node* curleft = cur->_left;
		Node* ppnode = parent->_parent;

		parent->_left = curleft;
		if (curleft)
		{
			curleft->_parent = parent;
		}
		cur->_right = parent;
		parent->_parent = cur;

		if (ppnode == nullptr)
		{
			_root = cur;
		}
		else
		{
			if (ppnode->_left = parent)
			{
				ppnode->_left = cur;
			}
			else
			{
				ppnode->_right = cur;
			}
		}
	}

	void RotateR(Node* parent)
	{
		Node* cur = parent->_left;
		Node* curright = cur->_right;
		Node* ppnode = parent->_parent;

		parent->_right = curright;
		if (curright)
		{
			curright->_parent = parent;
		}

		cur->_left = parent;
		parent->_parent = cur;


		if (ppnode == nullptr)
		{
			_root = cur;
		}
		else
		{
			if (ppnode->_left = parent)
			{
				ppnode->_left = cur;
			}
			else
			{
				ppnode->_right = cur;
			}
		}
	}
};

4.3红黑树插入及验证的代码实现

#include"RBTree.h"
#include"AVLTree.h"
#include
int main()
{
	int arr[] = { 4,2,6,1,3,5,15,7,16,14 };
	RBTree<int, int> rb;
	for (auto e : arr)
	{
 		rb.insert(make_pair(e,e));
		cout << "insert:" << e << "->" << rb.isBalance() << endl;
	}

	//int arr[] = { 4,2,6,1,3,5,15,7,16,14 };
	//AVLTree at;
	//for (auto e : arr)
	//{
	//	at.insert(make_pair(e, e));
	//	cout << "insert:" << e << "->" << at.isBalance() << endl;
	//}

	//随机数测试(RBTree)
	const int N = 10000;
	srand((unsigned)time(0));
	RBTree<int, int> rb;
	for (int i = 0; i < N; i++)
	{
		rb.insert(make_pair(rand(), rand()));

	}
	cout << rb.isBalance() << endl;


	随机数测试(AVLTree)
	//const int N = 10000;
	//srand((unsigned)time(0));
	//AVLTree at;
	//for (int i = 0; i < N; i++)
	//{
	//	at.insert(make_pair(rand(), rand()));

	//}
	//cout << at.isBalance() << endl;

	return 0;
}