c语言邻接表存储拓扑排序,拓扑排序(完整案列及C语言完整代码实现)
写在前面:博主是一位普普通通的19届双非软工在读生,平时最大的爱好就是听听歌,逛逛B站。博主很喜欢的一句话花开堪折直须折,莫待无花空折枝:博主的理解是头一次为人,就应该做自己想做的事,做自己不后悔的事,做自己以后不会留有遗憾的事,做自己觉得有意义的事,不浪费这大好的青春年华。博主写博客目的是记录所学到的知识并方便自己复习,在记录知识的同时获得部分浏览量,得到更多人的认可,满足小小的成就感,同时在写博客的途中结交更多志同道合的朋友,让自己在技术的路上并不孤单。
1.全序和偏序
拓扑排序指的是将有向无环图(又称“DAG”图)中的顶点按照图中指定的先后顺序进行排序。
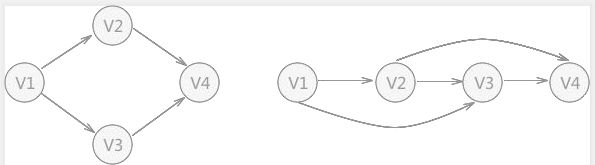
例如,上图 中的两个图都是有向无环图,都可以使用拓扑排序对图中的顶点进行排序,两个图形的区别是:左图中的 V2 和 V3之间没有明确的前后顺序;而右图中任意两个顶点之间都有前后顺序。
所以,左图中顶点之间的关系被称为“偏序”关系;右图中顶点之间的关系被称为”全序“关系。全序是偏序的一种特殊情况。对于任意一个有向无环图来说,通过拓扑排序得到的序列首先一定是偏序,如果任意两个顶点都具有前后顺序,那么此序列是全序。
2.拓扑排序的方法
对有向无环图进行拓扑排序,只需要遵循两个原则:
在图中选择一个没有前驱的顶点 V;
从图中删除顶点 V 和所有以该顶点为尾的弧
上面左图拓扑排序如下:
对于此图来说,拓扑排序有两种:
1.V1 -> V2 -> V3 -> V4
2.V1 -> V3 -> V2 -> V4
如果顶点之间只是具有偏序关系,那么拓扑排序的结果肯定不唯一;如果顶点之间是全序关系,那么拓扑排序得到的序列唯一
有向无环图如果顶点本身具有某种实际意义,例如用有向无环图表示大学期间所学习的全部课程,每个顶点都表示一门课程,有向边表示课程学习的先后次序,例如要先学《程序设计基础》和《离散数学》,然后才能学习《数据结构》。所以用来表示某种活动间的优先关系的有向图简称为“AOV 网”。
3.拓扑排序C语言完整代码实现
在编写程序解决拓扑排序的问题时,大致思路为:首先通过邻接表将 AOV 网进行存储,由于拓扑排序的整个过程中,都是以顶 点的入度为依据进行排序,所以需要根据建立的邻接表统计出各顶点的入度。 在得到各顶点的入度后,首先找到入度为 0 的顶点作为拓扑排序的起始点,然后查找以该顶点为起始点的所有顶点,如果入度 为 1,说明如果删除前一个顶点后,该顶点的入度为 0,为拓扑排序的下一个对象
#include
#include
#define MAX_VERTEX_NUM 20//最大顶点个数
#define VertexType int//顶点数据的类型
typedef enum{false,true} bool;
typedef struct ArcNode{
int adjvex;//邻接点在数组中的位置下标
struct ArcNode * nextarc;//指向下一个邻接点的指针
}ArcNode;
typedef struct VNode{
VertexType data;//顶点的数据域
ArcNode * firstarc;//指向邻接点的指针
}VNode,AdjList[MAX_VERTEX_NUM];//存储各链表头结点的数组
typedef struct {
AdjList vertices;//图中顶点及各邻接点数组
int vexnum,arcnum;//记录图中顶点数和边或弧数
}ALGraph;
//找到顶点对应在邻接表数组中的位置下标
int LocateVex(ALGraph G,VertexType u){
for (int i=0; i
if (G.vertices[i].data==u) {
return i;
}
}return -1;
}
//创建 AOV 网,构建邻接表
void CreateAOV(ALGraph **G){
*G=(ALGraph*)malloc(sizeof(ALGraph));
scanf("%d,%d",&((*G)->vexnum),&((*G)->arcnum));
for (int i=0; ivexnum; i++) {
scanf("%d",&((*G)->vertices[i].data));
(*G)->vertices[i].firstarc=NULL;
}
VertexType initial,end;
for (int i=0; iarcnum; i++) {
scanf("%d,%d",&initial,&end);
ArcNode *p=(ArcNode*)malloc(sizeof(ArcNode));
p->adjvex=LocateVex(*(*G), end);
p->nextarc=NULL;
int locate=LocateVex(*(*G), initial);
p->nextarc=(*G)->vertices[locate].firstarc;
(*G)->vertices[locate].firstarc=p;
}
}
//结构体定义栈结构
typedef struct stack{
VertexType data;
struct stack * next;
}stack;
//初始化栈结构
void initStack(stack* *S){
(*S)=(stack*)malloc(sizeof(stack));
(*S)->next=NULL;
}
//判断链表是否为空
bool StackEmpty(stack S){
if (S.next==NULL) { return true;
}return false;
}
//进栈,以头插法将新结点插入到链表中
void push(stack *S,VertexType u){
stack *p=(stack*)malloc(sizeof(stack));
p->data=u;
p->next=NULL;
p->next=S->next;
S->next=p;
}
//弹栈函数,删除链表首元结点的同时,释放该空间,并将该结点中的数据域通过地址传值给变量 i; void pop(stack *S,VertexType *i){
stack *p=S->next;
*i=p->data;
S->next=S->next->next;
free(p);
}
//统计各顶点的入度
void FindInDegree(ALGraph G,int indegree[]){
//初始化数组,默认初始值全部为 0
for (int i=0; i
indegree[i]=0;
}
//遍历邻接表,根据各链表中结点的数据域存储的各顶点位置下标,在 indegree 数组相应位置+1
for (int i=0; i
ArcNode *p=G.vertices[i].firstarc;
while (p) {
indegree[p->adjvex]++;
p=p->nextarc;
}
}
}
void TopologicalSort(ALGraph G){
int indegree[G.vexnum];//创建记录各顶点入度的数组
FindInDegree(G,indegree);//统计各顶点的入度
//建立栈结构,程序中使用的是链表
stack *S;
initStack(&S);
//查找度为 0 的顶点,作为起始点
for (int i=0; i
if (!indegree[i]) {
push(S, i);
}
}
int count=0;
//当栈为空,说明排序完成
while (!StackEmpty(*S)) {
int index;
//弹栈,并记录栈中保存的顶点所在邻接表数组中的位置
pop(S,&index);
printf("%d",G.vertices[index].data);
++count;
//依次查找跟该顶点相链接的顶点,如果初始入度为 1,当删除前一个顶点后,该顶点入度为 0
for (ArcNode *p=G.vertices[index].firstarc; p; p=p->nextarc) {
VertexType k=p->adjvex;
if (!(--indegree[k])) {
//顶点入度为 0,入栈
push(S, k);
}
}
}
//如果 count 值小于顶点数量,表明该有向图有环
if (count
printf("该图有回路"); return;
}
}
int main(){
ALGraph *G;
CreateAOV(&G);//创建 AOV 网
TopologicalSort(*G);//进行拓扑排序
return 0;
}
对于下面例子
进行拓扑排序:
//输入
6,8
1
2
3
4
5
6
1,2
1,4
1,3
3,2
3,5
4,5
6,4
6,5
//输出
6 1 4 3 2 5
4.拓扑排序小结
对于含有n个顶点和e条边的有向图而言,建立求各个顶点的入度的时间复杂度为O(e);建立0入度顶点栈的时间复杂度为O(n),在拓扑排序中若有向图无环,则每个顶点进一次栈出一次栈,所以总的时间复杂度为O(n+e)
来源:oschina
链接:https://my.oschina.net/u/4386188/blog/4503316