pcl--第四节 采样一致性算法RANSAC

RANSAC随机采样一致性算法简介

RANSAC是“RANdom SAmple Consensus”（随机抽样共识或采样一致性）的缩写，它是一种迭代方法，用于从包含异常值的一组数据中估计数学模型的参数。该算法由Fischler和Bolles于1981年发布。

RANSAC算法假定我们要查看的所有数据均由内部值和异常值组成。可以用带有一组特定参数值的模型来解释离群值，而离群值在任何情况下都不适合该模型。其过程可以从数据中估计所选模型的最佳参数。

RANSAC是一种随机参数估计算法。RANSAC 从样本中随机抽选出一个样本子集,使用最小方差估计算法对这个子集计算模型参数，然后计算所有样本与该模型的偏差,再使用一个预先设定好的阑值与偏差比较，当偏差小于闽值时,该样本点属于模型内样本点(inliers),文中简称局内点或内点，否则为模型外样本点(outliers).文中简称局外点或外点,记录下当前的 inliers 的个数，然后重复这一过程。每一次重复都记录当前最佳的模型参数,所谓最佳即是inliers 的个数最多此时对应的 inliers 个数为 best_ninliers。每次迭代的末尾都会根据期望的误差率best_ninliers总样本个数、当前迭代次数,计算一个迭代结束评判因子,据此决定是否迭代结束迭代结束后,最佳模型参数就是最终的模型参数估计值。

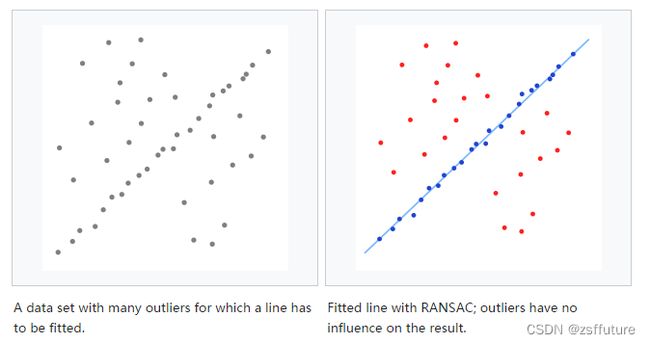
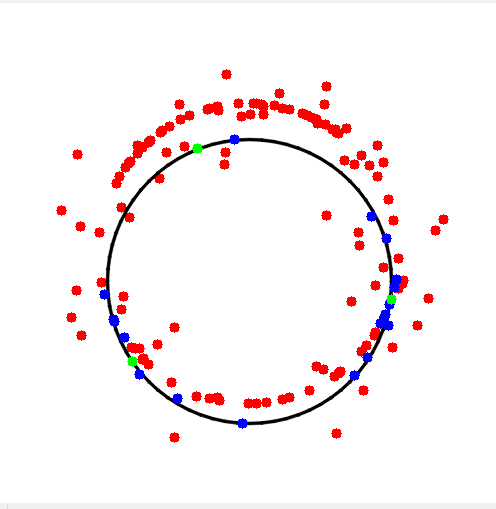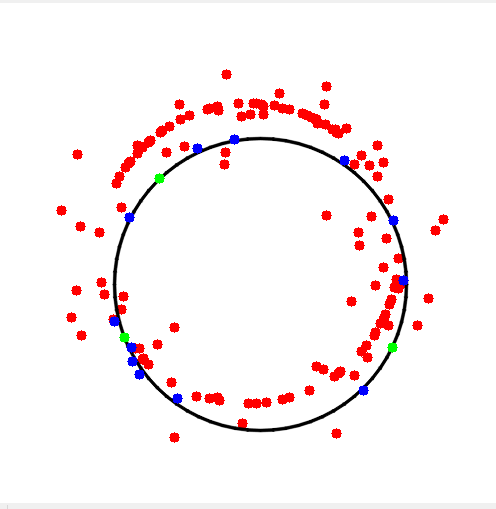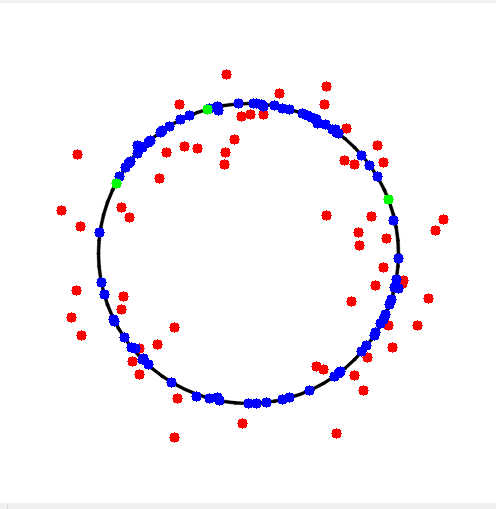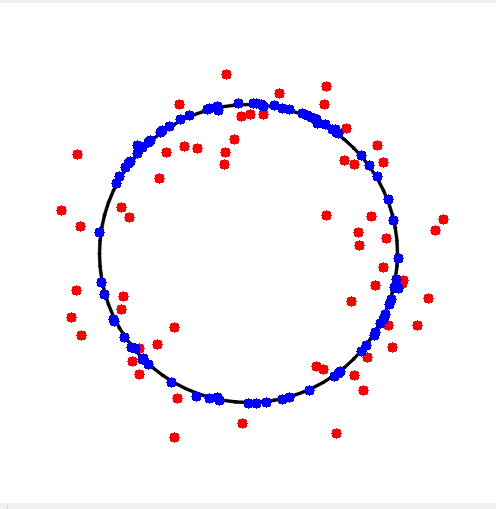
RANSAC理论上可以剔除 outliers 的影响,并得到全局最优的参数估计。但是RANSAC有两个问题首先在每次迭代中都要区分inliers和outlieres,因此需要事先设定阙值,当模型具有明显的物理意义时,这个阙值还比较容易设定,但是若模型比较抽象时,这个阙值就不那么容易设定了，而且固定值不适用于样本动态变化的应用;第二个问题是,RANSAC 的选代次数是运行期决定的,不能预知选代的确切次数(当然迭代次数的范围是可以预测的)。除此之外,RANSAC 只能从一个特定数据集中估计一个模型，当两个(或者更多个)模型存在时，RANSAC不能找到别的模型图a和b展示了 RANSAC算法在二维数据集中的简单应用。图a的图像形象地表示了一组既包含局内点又包含局外点的数据集。图 b的图像中所有的局外点都表示为红色,局内点表示为蓝色，蓝色线就是基于 RANSAC得到的结果，此例中我们尝试适应数据的模型就是一条线。

同理还可以拟合圆

 

PCL 中以随机采样一致性算法( RANSAC) 为核心，实现了五种类似于RANSAC的随机参数估计算法，例如随机采样一致性估计（RANSAC ) 、最大似然一致性估计 （MLESAC ) 、最小中值方差一致性估计 ( LMEDS )等，所有的估计参数算法都符合一致性准则。利用RANSAC可以实现点云分割，目前 PCL 中支持的几何模型分割有 空间平面、直线、二维或三维圆、圆球、锥体等 。 RANSAC的另一应用就是点云的配准对的剔除。 

LMedS最小中值方差估计算法

LMedS也是一种随机参数估计算法。LMedS也从样本中随机抽选出一个样本子集,使用最小方差估计算法对子集计算模型参数，然后计算所有样本与该模型的偏差。但是与 RANSAC不同的是,LMedS 记录的是所有样本中偏差值居中的那个样本的偏差,称为 Med 偏差(这也是 LMedS 中 Med 的由来以及本次计算得到的模型参数。由于这一变化,LMedS 不需要预先设定值来区分inliers 和outliers。重复前面的过程N次,从中N个 Med 偏差中挑选出最小的一个,其对应的模型参数就是最终的模型参数估计值。其中迭代次数 N 是由样本子集中样本的个数期望的模型误差、事先估计的样本中outliers 的比例所决定。
LMedS理论上也可以剔除 outliers 的影响并得到全局最优的参数估计而且克服了RANSAC的两个缺点(虽然 LMedS 也需要实现设定样本中 outliers 的比例 ，但这个数字比较容易设定。但是当 outliers 在样本中所占比例达到或超过50%时，LMedS就无能为力了!这与 LMedS每次代记录的是“Med”偏差值有关。

RANSAC随机采样原理

RANSAC从样本中随机抽选出一个样本子集，使用最小方差估计算法对这个子集计算模型参数，然后计算所有样本与该模型的偏差，再使用一个预先设定好的阈值与偏差比较，当偏差小于阈值时，该样本点属于模型内样本点 ( inliers），或称内部点、局内点或内点，否则为模型外样本点（outliers），或称外部点、局外点或外点，记录下当前的 inliers 的个数，然后重复这一过程。每一次重复都记录当前最佳的模型参数，所谓最佳即是inliers的个数最多 ，此时对应的inliers个数为 best_ninliers 。 每次迭代的末尾都会根据期望的误差率、 best_ninliers、总样本个数、当前迭代次数，计算一 个迭代结束评判因子，据此决定是否迭代结束。迭代结束后，最佳模型参数就是最终的模型参数估计值 。

RANSAC理论上可以剔除outliers的影响，并得到全局最优的参数估计。但是RANSAC 有两个问题，首先在每次迭代中都要区分 inliers 和 outlieres，因此需要事先设定阈值，当模型具有明显的物理意义时，这个阈值还比较容易设定，但是若模型比较抽象时，阈值就不那么容易设定了。而且固定阈值不适用于样本动态变化的应用；第二个问题是，RANSAC的迭代次数是运行期决定的，不能预知迭代的确切次数（当然迭代次数的范围是可以预测的）。除此之外， RANSAC 只能从一个特定数据集中估计一个模型，当两个（或者更多个）模型存在时，RANSAC 同时找到多个模型。

#include 
#include 

#include 
#include  // for PointCloud
#include  // for copyPointCloud
#include 
#include 
#include 
#include 
#include 
#include 

using namespace std::chrono_literals;

pcl::visualization::PCLVisualizer::Ptr
simpleVis (pcl::PointCloud::ConstPtr cloud)
{
  // --------------------------------------------
  // -----Open 3D viewer and add point cloud-----
  // --------------------------------------------
  pcl::visualization::PCLVisualizer::Ptr viewer (new pcl::visualization::PCLVisualizer ("3D Viewer"));
  viewer->setBackgroundColor (0, 0, 0);
  viewer->addPointCloud (cloud, "sample cloud");
  viewer->setPointCloudRenderingProperties (pcl::visualization::PCL_VISUALIZER_POINT_SIZE, 3, "sample cloud");
  //viewer->addCoordinateSystem (1.0, "global");
  viewer->initCameraParameters ();
  return (viewer);
}

int
main(int argc, char** argv)
{
  // initialize PointClouds
  pcl::PointCloud::Ptr cloud (new pcl::PointCloud);
  pcl::PointCloud::Ptr final (new pcl::PointCloud);

  // populate our PointCloud with points
  cloud->width    = 500;
  cloud->height   = 1;
  cloud->is_dense = false;
  cloud->points.resize (cloud->width * cloud->height);
  for (pcl::index_t i = 0; i < static_cast(cloud->size ()); ++i)
  {
    if (pcl::console::find_argument (argc, argv, "-s") >= 0 || pcl::console::find_argument (argc, argv, "-sf") >= 0)
    {
      (*cloud)[i].x = 1024 * rand () / (RAND_MAX + 1.0);
      (*cloud)[i].y = 1024 * rand () / (RAND_MAX + 1.0);
      if (i % 5 == 0)
        (*cloud)[i].z = 1024 * rand () / (RAND_MAX + 1.0);
      else if(i % 2 == 0)
        (*cloud)[i].z =  sqrt( 1 - ((*cloud)[i].x * (*cloud)[i].x)
                                      - ((*cloud)[i].y * (*cloud)[i].y));
      else
        (*cloud)[i].z =  - sqrt( 1 - ((*cloud)[i].x * (*cloud)[i].x)
                                        - ((*cloud)[i].y * (*cloud)[i].y));
    }
    else
    {
      (*cloud)[i].x = 1024 * rand () / (RAND_MAX + 1.0);
      (*cloud)[i].y = 1024 * rand () / (RAND_MAX + 1.0);
      if( i % 2 == 0)
        (*cloud)[i].z = 1024 * rand () / (RAND_MAX + 1.0);
      else
        (*cloud)[i].z = -1 * ((*cloud)[i].x + (*cloud)[i].y);
    }
  }

  pcl::PCDWriter writer;
  writer.write("data.pcd", *cloud);


  std::vector inliers;

  // created RandomSampleConsensus object and compute the appropriated model
  pcl::SampleConsensusModelSphere::Ptr
    model_s(new pcl::SampleConsensusModelSphere (cloud));
  pcl::SampleConsensusModelPlane::Ptr
    model_p (new pcl::SampleConsensusModelPlane (cloud));
  if(pcl::console::find_argument (argc, argv, "-f") >= 0)
  {
    pcl::RandomSampleConsensus ransac (model_p);
    ransac.setDistanceThreshold (.01);
    ransac.computeModel();
    ransac.getInliers(inliers);
  }
  else if (pcl::console::find_argument (argc, argv, "-sf") >= 0 )
  {
    pcl::RandomSampleConsensus ransac (model_s);
    ransac.setDistanceThreshold (.01);
    ransac.computeModel();
    ransac.getInliers(inliers);
  }

  // copies all inliers of the model computed to another PointCloud
  pcl::copyPointCloud (*cloud, inliers, *final);
  writer.write("plane.pcd", *final);
  // creates the visualization object and adds either our original cloud or all of the inliers
  // depending on the command line arguments specified.
  pcl::visualization::PCLVisualizer::Ptr viewer;
  if (pcl::console::find_argument (argc, argv, "-f") >= 0 || pcl::console::find_argument (argc, argv, "-sf") >= 0)
    viewer = simpleVis(final);
  else
  {
      viewer = simpleVis(cloud);
  }
    
  while (!viewer->wasStopped ())
  {
    viewer->spinOnce (100);
    std::this_thread::sleep_for(100ms);
  }
  return 0;
 }

我这边把例子数据进行了保存，然后可视化，结果如下