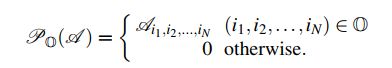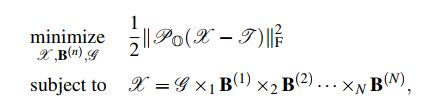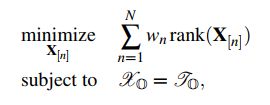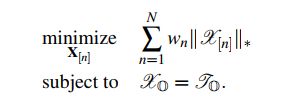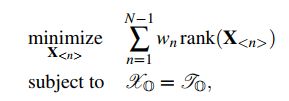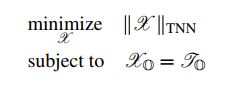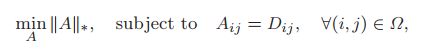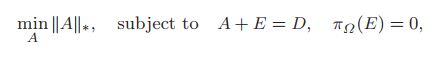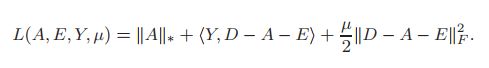张量（四）：张量补全（tensor completion）
现实情况下，往往由于采集数据工具（如采集交通数据的传感器）的故障以及其他异常情况导致数据中往往存在部分缺失值，对这些缺失值的修补称之为“补全”，张量领域的缺失值修复即张量补全。张量补全是根据已有数据对缺失值的影响和低秩假设实现缺失值补全，主要分为两类方法：
- 一种是基于张量补全中给定的秩和更新因子
- 一种是直接最小化张量秩并更新低秩张量
到此还一脸懵逼的读者可以先行跳到第三章，先行阅读矩阵补全的内容。
目录
1 基于张量分解的方法
1.1 基于CP分解
1.2 基于Tucker分解
1.3 基于张量链分解
1.4 基于张量环分解
1.5 基于t-SVD分解
2 秩最小化模型
2.1 Tucker秩最小化模型
2.2 张量链秩最小化模型
2.3 管秩最小化模型
3 矩阵补全
1 基于张量分解的方法
基于张量分解的张量补全可转化为如下优化问题（大多数的张量补全问题都可转化为对优化问题的求解）：
其中，X是补全后的张量，J是原始存在缺失值的张量。不同张量分解方法对张量补全带来的差异主要集中于秩的定义，如CP分解，Tucker分解等。S是一个给定的低秩张量X的秩的界限。
表示随机取样操作，定义为：
关于优化问题的意义可参考我的上篇文章张量（三）。
1.1 基于CP分解
以CP分解的秩代替张量补全中的秩，原优化问题转化为：
该问题可通过交替最小二乘法（ALS）解决，即每轮迭代通过其他固定变量去更新单个变量。但是，这个模型是非凸的，会受到局部最小值的影响，需要良好的初始化才能得到比较好的效果。此外一些最新的方法比如CPWOPT、geomCG也被提出去解决这些问题。
1.2 基于Tucker分解
以Tucker分解的秩代替张量补全的秩，原优化问题转化为：
其中g为核心张量，B为因子矩阵。该问题同样可通过ALS解决，并通过高阶正交迭代（HOOI）加速运行，迭代计算正交因子矩阵一列对应的主导奇异向量。
此外，一种推广的张量补全模型十分流行，它拥有一种预定义的Tucker秩，优化问题如下：
其中t是观测数据，P是线性操作符。这个问题可通过张量迭代硬阈值（TIHT）解决，该方法采用截断的高阶奇异值分解作为阈值算子，得到最优的低阶张量逼近。
1.3 基于张量链分解
以张量链分解的秩代替张量补全的秩，原优化问题转化为：
这个问题是非凸的，并且存在拟最优逼近解，可以通过使用非线性块高斯-塞德尔迭代进行计算。对于每个小块，都可以采用最小二乘拟合的方法进行求解，从而加快收敛速度。此外，在张量链秩固定的情况下，可以在黎曼优化框架内使用非线性共轭梯度方案来解决该问题，该方案可以使复杂度随维数的变化呈线性变化。
1.4 基于张量环分解
低秩张量环补全是唯一一个有着固定张量环秩的张量补全方法。优化问题如下：
其中
意思是
，
。张量链的秩表示大多中间因子的分布和少部分边界因子的分布。张量环分解可以有效解决张量链分解的缺陷。在初始点选择良好的情况下，用ALS法可以解决此优化问题。
1.5 基于t-SVD分解
使用t-SVD分解的管秩代替张量补全的秩，原优化问题转化为：
该问题可通过将目标张量分解为两个低管秩张量的循环卷积来解决。因此，优化问题可进一步改进为：
其中
，
，该低管秩张量补全模型可通过交替最小化算法解决。
2 秩最小化模型
在实际中，张量秩界可能在一些应用中是不可用的。当观测值很少时，高秩界的选择可能会导致过拟合。为了避免这种情况发生，另一种方法是直接最小化张量的秩。其优化问题如下：
其中
意思是
，
均属于观测值索引。rank(X)表示张量秩，可以有多种定义，如CP分解的秩，Tucker分解的秩等。根据不同张量秩的定义，存在多种张量补全问题的优化模型。然而，由于rank是一个非凸函数，因此优化问题变成了一个NP难问题。大多数现有的方法都是使用核范数（迹范数）替代非凸的秩函数。但是，CP分解的张量核范数是不可解的且张量环的核范数未曾迁移到张量补全的问题中，因此下面对这两种模型不予讨论。
2.1 Tucker秩最小化模型
基于最小化Tucker秩的张量补全优化模型如下：
其中，，![rank\left ( X_{\left [ n \right ]} \right )](http://img.e-com-net.com/image/info8/3fd1fb60d82d463b858fb7a1a919830a.gif){kind=small}
表示![X_{\left [ n \right ]}](http://img.e-com-net.com/image/info8/fb1357360dee4933bec94d91cedefcc0.gif){kind=small}
的展开矩阵的秩。基于Tucker秩的定义，优化问题可进一步转化为：
实际上，矩阵秩函数在优化问题中是非凸的，但可以转化为矩阵核范数近似。于是优化问题进一步转化为：
该问题可用简单的低秩张量补全（SiLRTC）来解决，也可通过增加一个方程约束，用高精度的低秩张量补全（HaLRTC）来严格解决。
2.2 张量链秩最小化模型
基于最小化张量链秩的张量补全优化模型如下：
其中，
表示
的展开矩阵的秩。因此，原优化问题可进一步转化为：
该优化问题可通过矩阵核范数近似，进一步转化为：
该问题可通过简单的低秩张量补全，借助张量链（SiLRTC-TT）来解决。
2.3 管秩最小化模型
基于最小化张量管秩的张量补全优化模型如下：
其中，张量管道秩定义为J的非零奇异管道数量，J来源于t-SVD分解，
。原优化问题可进一步改进为：
是X的核范数，等价于
的核范数，blkdiag定义见张量（二）。最新的一些模型为了更好地估计张量管秩，提出了一些新的凸包络，如张量截断核范数（T-TNN）和加权张量核范数（W-TNN）来代替传统的TNN。
3 矩阵补全
矩阵补全问题可以看做是矩阵恢复问题的一种特殊情况，在已知矩阵项数有限的情况下，需要恢复矩阵中缺失的项。可通过如下优化问题来完成矩阵恢复：
矩阵补全问题可转为下式：
即在保证A+E=D和
中的输入不改变以及之外的数据为0的前提下，实现A的核范数最小化。该优化问题可通过ALM来解决，拉格朗日函数为：
算法流程如下：
