R语言预测海藻频率（多元线性回归、回归树、组合随机森林）

背景介绍

背景：河流中海藻的集中爆发不仅会对河流的生态环境造成破坏，还会影响河流的水质。
需求：基于以往的观测数据，对河流中海藻的爆发情况进行预测并采取必要防范措施以提高河流的水质量。
方法：以海藻样本数据为数据集，通过数据挖掘的方式分析影响海藻爆发的主要因素，并通过构建预测模型，对海藻的爆发情况进行事先预测。
结合刚刚学习R语言，进行分析

数据集加载

通过DMwR包来对海藻数据进行加载，并设定表头等数据。如图1所示：
第一个数据集有200个水样。该数据集的每一条记录是同一条河流在该年的同一个季节的三个月内收集的水样的平均值。每条记录由11个变量构成。其中3个变量是名义变量，它们分别描述水样收集的季节、收集河流的大小和河水速度。余下的8个变量是所观察水样的不同化学参数，即最大pH值、最小含氧量（O2）、平均氯化物含量(cl)、平均硝酸盐含量(NO3)、平均氨含量(NH4)、平均正磷酸含量(PO4)、平均磷酸盐含量(PO4)、平均叶绿素含量。

数据集中的数据分析

数据分析:

对数据进行分析，可以得到不同季节的河流速度，大小。以及不同元素的最小值、平均值、最大值等等要素。图2所示：

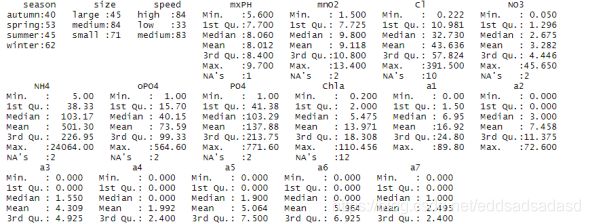
可视化分析:
绘制PH直方图加密度图，用QQ图查看数据是否符合正态分布。

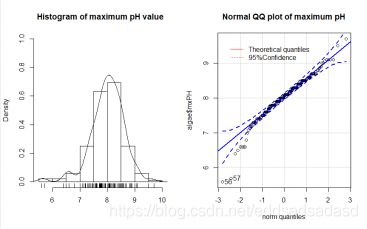
左图可以看出变量maximum PH基本呈正态分布，符合统计分析的需要。右图为mxPH变量值和正态分布的理论分位数（红色实线）的点散图。同时给出了正态分布95%置信区间的带状图（虚线），可以看出左下有几个小点明显在95%置信区间之外，不服从正态分布。
绘制河流的pH值在不同水体中的分布情况，可以分析其平均值，最小值和最大值等特征。

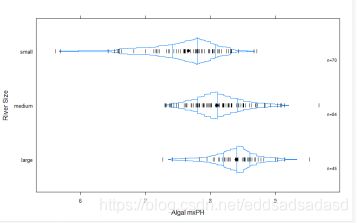
小型河流有更高的海藻频率。但小型河流海藻频率的分布比其他类型河流的海藻频率分布更分散。
变量分析:
在原有的基础上对于变量opO4进行分析，观察变量的变化情况，如图所示：

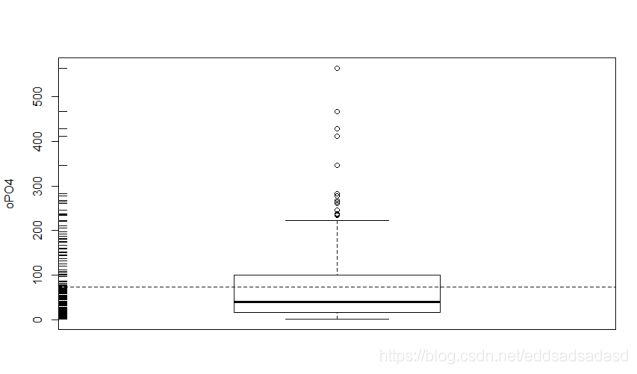
由图可知，变量oPO4的分布集中在较小的观察值范围，大部分水样的oPO4值比较低，但也有几个水样的观测值较高，甚至特别高。

无效数据处理

剔除多余数据，并可利用最高频值填补缺失值、通过变量的相关关系来填补缺失值、通过线性相关po4和opo4值的关系填补缺失值等等。

预测模型的构建

多元线性回归模型:
多元线性回归模型通常用来研究一个应变量依赖多个自变量的变化关系，如果二者的以来关系可以用线性形式来刻画，则可以建立多元线性模型来进行分析。

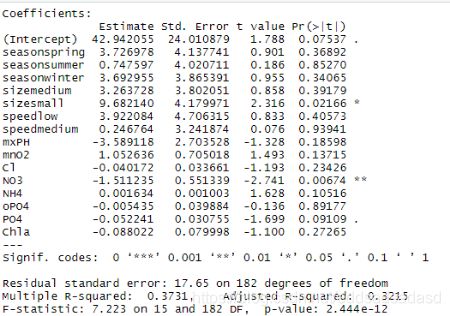
平方系数0.3215，并不是很理想
回归树模型预测：
回归决策树（目标变量为连续型变量），通过决策树的生长和决策树的修剪，根据已知预测、归类未来。

组合的随机森林模型：
随机森林，是用随机的方式建立一个森林，森林里面有很多的决策树组成，随机森林的每一棵决策树之间是没有关联的。在得到森林之后，当有一个新的输入样本进入的时候，就让森林中的每一棵决策树分别进行一下判断，看看这个样本应该属于哪一类（对于分类算法），然后看看哪一类被选择最多，就预测这个样本为那一类。
在建立每一棵决策树的过程中，首先是两个随机采样的过程，random forest对输入的数据要进行行、列的采样。对于行采样，采用有放回的方式，也就是在采样得到的样本集合中，可能有重复的样本。假设输入样本为N个，那么采样的样本也为N个。这样使得在训练的时候，每一棵树的输入样本都不是全部的样本，使得相对不容易出现over-fitting。然后进行列采样，从M个feature中，选择m个(m << M)。之后就是对采样之后的数据使用完全分裂的方式建立出决策树，这样决策树的某一个叶子节点要么是无法继续分裂的，要么里面的所有样本的都是指向的同一个分类。一般很多的决策树算法都一个重要的步骤—剪枝，但是这里不这样实行，由于之前的两个随机采样的过程保证了随机性，所以就算不剪枝，也不会出现over-fitting。
这种算法，得到随机森林中的每一棵树都是很弱的，但是组合起来性能很高。

模型的评价与选择

多元线性回归模型：
首先，将多元线性回归模型预测值与实测值比较，发现模拟效果较差。如下图所示：

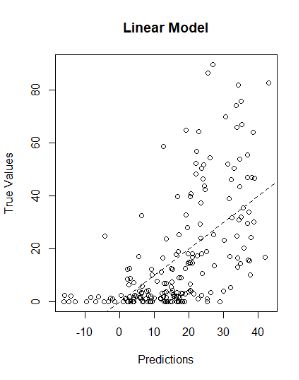
其次，评价模型的稳定性。对于线性回归模型来讲，平均绝对误差为13.10681
回归树模型：
首先，将回归树模型预测值与实测值比较，发现模拟效果较差。如下图 所示：

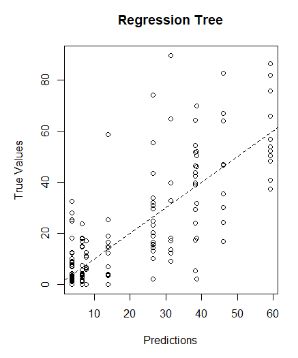
其次，评价模型的稳定性。对于回归树模型来讲，平均绝对误差为8.480619。
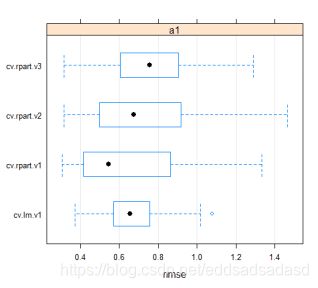
NMSE是一个比值，其取值范围通常为0~1 。如果模型表现优于这个非常简单基准模型预测，那么NMSE应明显小于1。NMSE的值越小，模型的性能就越好。下图中，cv.rpart.v1效果更好。即除了海藻1外，其他的海藻的预测结果都不理想。


组合随机森林模型：
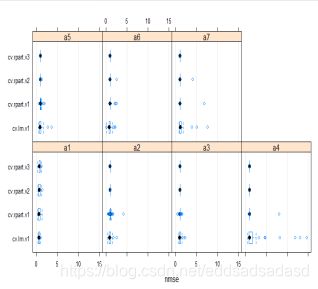
通过R语言，组合随机森林模型计算过程输出比较长，可以得到对7中海藻的预测值分析，如下图所示：

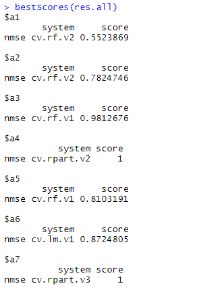
可以看出随机森林的总体结果最好，但对海藻7和海藻4并不理想。

海藻爆发频率预测

将原有的algea作为训练数据集，获得所有7个模型,利用随机森林模型进行预测分析，并计算模型NMSE值。结果如下图所示：

得到的结果与前面模型的交叉验证结果相一致。同此确认了很难得到的海藻7较好的预测，海藻1的估计结果最佳。
综上所述，结合多元线性回归模型、回归树模型、组合随机森林模型，其中，组合随机森林模型的预测效果较好，其次为回归树模型，多元线性回归模型较差。

```ruby
#数据集的加载
library(DMwR)
data("algae")
head(algae)

#数据分析
summary(algae)

#可视化的方式查看algae的统计信息
#查看字段的分别情况
library("car")
par(mfrow=c(1,2))
hist(algae$mxPH,prob=T,xlab = '', 
     main='Histogram of maximum pH value', ylim = 0:1)
lines(density(algae$mxPH,na.rm = T))
rug(jitter(algae$mxPH))
qqPlot(algae$mxPH, main='Normal QQ plot of maximum pH')
legend("topleft",inset=.05,
       legend=c("Theoretical quantiles", "95%Confidence"),
       lty=c(1,3),bty="n",col = c("red","red"))
par(mfrow=c(1,1))

#绘制河流的pH值在不同水体中的分布情况
library("Hmisc")
bwplot(size~mxPH,data = algae,panel = panel.bpplot,
       probs=seq(.01,.49,by=.01),datadensity=TRUE,
       ylab='River Size',xlab='Algal mxPH')
#OPO4变量分析
boxplot(algae$oPO4,ylab="oPO4")
rug(jitter(algae$oPO4),side = 2)
abline(h= mean(algae$oPO4,na.rm = T),lty =2)

#无效数据的处理
data("algae")
nrow(algae)
algae<-na.omit(algae)
nrow(algae)

#基于类数据分析的无效数据填充
data("algae")
algae[48,]
algae[48,"mxPH"]<-mean(algae$mxPH,na.rm=T)
algae[48,]

cor(algae[,4:18],use = "complete.obs")
symnum(cor(algae[,4:18],use="complete.obs"))

data("algae")
algae<-algae[-manyNAs(algae),]
nrow(algae)

algae[28,]
algae[28,"PO4"]<-42.897+1.293*algae[28,"oPO4"]
algae[28,]
algae<- knnImputation(algae,k=10,meth = "median")
#预测模型的构建,多元线性回归模型
data("algae")
algae<-algae[-manyNAs(algae),]
clean.algae<-knnImputation(algae,k=10)
lm.al<-lm(a1~.,data=clean.algae[,1:12])
summary(lm.al)

final.lm<-step(lm.al)
summary(final.lm)

#回归树模型预测
library(rpart)
data("algae")
algae<-algae[-manyNAs(algae),]
rt.al<-rpart(a1~.,data=algae[,1:12])
prettyTree(rt.al)
#组合随机森林模型GBDK
library (randomForest)
cv.rf<-function(form,train,test,...){
  m<-randomForest(form,train,...)
  p <- predict(m,test)
  mse <- mean((p-resp(form,test))^2)
  c(nmse=mse/mean((mean(resp(form,train))-resp(form,test))^2))
}
res.all <- experimentalComparison(
  DSs,
  c(variants("cv.lm"),
    variants("cv.rpart",se=c(0,0.5,1)),
    variants("cv.rf",ntree=c(200,500,700))
  ),
  cvSettings(5,10,1234))
bestScores(res.all)
#模型的评价与选择
lm.predictions.al<-predict(final.lm,clean.algae)
rt.predictions.al<-predict(rt.al,algae)
mae.al.lm<-mean(abs(lm.predictions.al-algae[,"a1"]))
mae.al.rt<-mean(abs(rt.predictions.al-algae[,"a1"]))
mae.al.lm
mae.al.rt
#绘制线性回归模型预测值与实测值比较
old.par<-par(mfrow=c(1,2))
plot(lm.predictions.al,algae[,"a1"],main="Linear Model",
     xlab="Predictions", ylab="True Values")
abline(0,1,lty=2)
plot(rt.predictions.al,algae[,"a1"],main="Regression Tree",
     xlab="Predictions", ylab="True Values")
abline(0,1,lty=2)
par(old.par)

#评价模型的稳定性，以及模型的比较和选择
cv.rpart<-function(form,train,test,...){
  m<-rpartXse(form,train,...)
  p<-predict(m,test)
  mse<-mean((p-resp(form,test))^2)
  c(nmse=mse/mean((mean(resp(form,train))-resp(form,test))^2))
}
cv.lm<-function(form,train,test,...){
  m<-lm(form,train,...)
  p<-predict(m,test)
  p<-ifelse(p<0,0,p)
  mse<-mean((p-resp(form,test))^2)
  c(nmse=mse/mean((mean(resp(form,train))-resp(form,test))^2))
}
res<-experimentalComparison(
  c(dataset(a1~.,clean.algae[,1:12],'a1')),
  c(variants('cv.lm'),variants('cv.rpart',se=c(0,0.5,1))),
  cvSettings(3,10,1234))
plot(res)

#分析两个模型对7种海藻的爆发情况预测
DSs<-sapply(names(clean.algae)[12:18],
            function(x,names.attrs){
              f<-as.formula(paste(x,"~."))
              dataset(f,clean.algae[,c(names.attrs,x)],x)
            },
            names(clean.algae)[1:11])
res.all<-experimentalComparison(
  DSs,c(variants('cv.lm'),variants('cv.rpart',se=c(0,0.5,1))),
  cvSettings(5,10,1234)
)
bestScores(res.all)
#分析两个模型对7种海藻的爆发情况预测,画图分析
DSs<-sapply(names(algae)[12:18],
            function(x,names.attrs){
              f<-as.formula(paste(x,"~."))
              dataset(f,algae1[,c(names.attrs,x)],x)
            },
            names(algae)[1:11])
res.all<-experimentalComparison(
  DSs,c(variants("cv.lm"),),variants("cv.rpart",se=c(0,0.5,1)))
res.all<-experimentalComparison(
  DSs,c(variants("cv.lm"),variants("cv.rpart",se=c(0,0.5,1))),cvSettings(5,10,1234))
plot(res.all)

#海藻爆发率预测
bestModelsNames<-sapply(bestScores(res.all),function(x) x["nmse","system"])
learners<-c(rf="randomForest",rpart ="rpartXse",lm="lm")
funcs<-learners[sapply(strsplit(bestModelsNames,"\\."),function(x) x[2])]

parSetts<-lapply(bestModelsNames,function(x) getVariant(x,res.all)@pars) 
bestModels<-list()
for(j in 1:7){
  form=as.formula(paste(names(clean.algae)[11+j],'~.'))
  bestModels[[j]]=do.call(funcs[j],c(list(form,clean.algae[,c(1:11,11+j)]),parSetts[[j]]))}
clean.test.algae<-knnImputation(test.algae,k=10,distData=algae[,1:11])
#获取整个测试数据集的预测值矩阵
preds<-matrix(ncol=7,nrow=140)
for(i in 1:nrow(clean.test.algae))
  preds[i,]=sapply(1:7,function(x)
    predict(bestModels[[x]],clean.test.algae[i,]))
#计算NMSE值
avg.preds=apply(algae[,12:18],2,mean)
apply(((algae.sols-preds)^2), 2,mean)/apply((scale(algae.sols,avg.preds,F)^2),2,mean)