数据结构——堆

堆

1. 什么是堆

在树和二叉树一文中可以了解到：

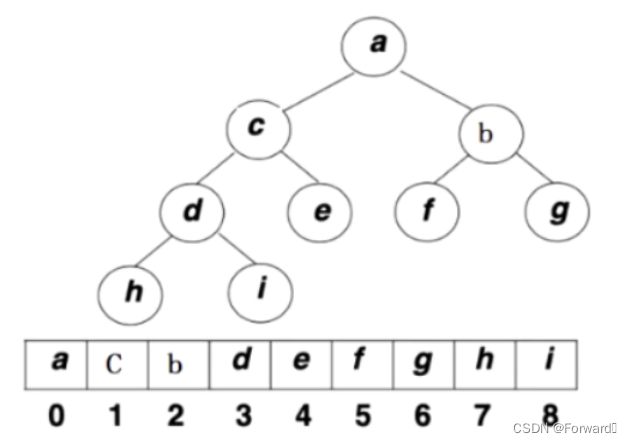
堆通常是一个可以被看作一棵完全二叉树的数组对象。

• 堆的逻辑结构是一棵完全二叉树
• 堆的物理结构是一个数组

如图所示：

---

2. 堆的两个特性

• 结构性：用数组表示的完全二叉树

• 有序性：任意节点的关键值是其子树所有节点的最大值（或最小值）

  • ”最大堆(MaxHeap)“，也叫”大顶堆“：最大值，即每棵子树的根节点的值都大于等于其子节点的值
  • ”最小堆(MaxHeap)“，也叫”小顶堆“：最小值，即每棵子树的根节点的值都小于等于其子节点的值

我们通过一道例题来加深对堆的理解：

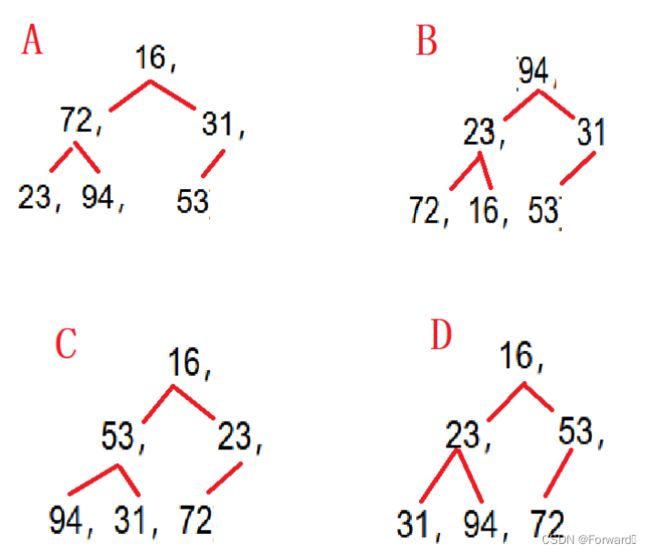
下列关键字序列中，序列 () 是堆
A.(16，72，31，23，94，53)
B.(94，23，31，72，16，53)
C.(16，53，23，94，31，72）
D.(16，23，53，31，94，72)

我们可以通过画图来分析：

通过分析我们可以知道，只有序列D符合堆的条件，其每个子树的父亲都小于它的孩子，因此这也是一个小堆。

---

3. 父子节点下标之间的关系

我们定义父亲为parent，左右孩子为leftchild, rightchild

• 我们可以通过数组的下标来确定父子节点的关系，结论如下

leftchild = parent * 2 + 1

rightchild = parent * 2 + 2

parent = (child - 1) / 2

---

4. 堆的实现

由于堆的物理存储结构是一个数组，因此我们可以像定义顺序表一样定义堆的结构：

typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	int size;	//记录当前数据个数
	int capacity;	//记录最大容量
}Heap;

4.1 堆的插入HeapPush

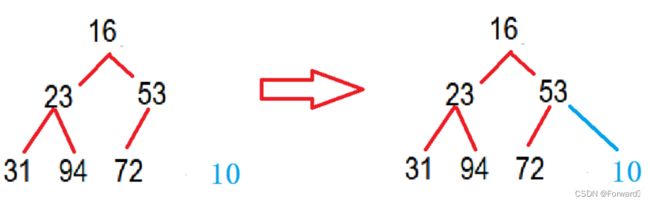
向堆中插入数据，在内存中也就相当于向一个数组插入数据，而为了确保效率，显然我们应该将新数据val插入到数组尾部。

如图所示：

此时我们发现，数据10插入后，这一串数据构成的完全二叉树就不满足堆的性质了。因此为了确保堆结构的正确性，每插入一次数据，我们都要重新对堆进行调整

4.1.1 向上调整算法AdjustUp：

调整的整体原则是：

• 如果原来是小堆，并且插入的数据val小于父亲parent，那么就将val和parent调换位置。继续向根部向上调整，直到满足所有的父亲小于等于它的孩子。

• 大堆同理。

例如：

4.1.2 AdjustUp代码实现（以大堆为例）

void AdjustUp(HPDataType* a, int child)
{
    //新插入数据的父亲
	int parent = (child - 1) / 2;

    //开始向上调整
	while (child > 0)
	{
        //如果孩子大于父亲，那就要交换
        //并继续向上调整
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);

			child = parent;
			parent = (parent - 1) / 2;
		}
		
        //否则说明已经符合堆的性质，退出循环
		else
			break;
	}
}

4.1.3 HeapPush实现

知道了如何向上调整，那么堆的插入就很简单了。只需要在插入新的数据后进行一次向上调整就行。

void HeapPush(Heap* hp, HPDataType x)
{
	//检查容量
	if (hp->size == hp->capacity)
	{
		hp->capacity *= 2;
		HPDataType* temp = (HPDataType*)realloc(hp->a, sizeof(HPDataType) * hp->capacity);
		if (NULL == temp)
		{
			perror("realloc");
			exit(-1);
		}
	}

	hp->a[hp->size] = x;
	hp->size++;

	AdjustUp(hp->a, hp->size - 1);
}

4.1.4 时间复杂度

对于每一次插入，向上调整时最多调整二叉树的高度次，假设二叉树有N个节点，那么它的高度h就是log₂(N+1)，即时间复杂度为O(logN)

4.2 堆的删除HeapPop

首先我们应该思考，对于构成堆的数组，我们应该删除数组的第一个元素还是最后一个元素？

可能有的小伙伴觉得为了使删除的效率最高，应该删除数组的最后一个元素，但是这种做法是没有任何意义的。

应该清楚，堆顶元素(即数组的首元素)要么是整个数组的最大值，要么是整个数组的最小值，因此对这一个数进行操作才能有较大的意义

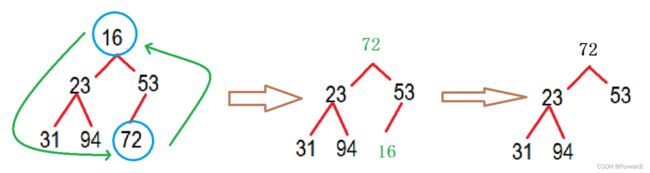
正确的删除操作HeapPop应该是这样的：

• 删除的数据应该是堆顶元素
• 将堆顶元素（即数组首元素）和数组最后一个元素调换位置
• 再删除最后一个元素

如图：

显然我们可以看到，和插入操作一样，删除操作后仍不能保证堆结构的正确性，因此我们仍需要重新对堆进行调整

4.2.1 向下调整算法AdjustDown

删除操作中我们将原来数组的最后一个元素放到了堆顶，从而导致堆顶数据不一定满足堆的条件，因此我们也要从堆顶开始向下调整。

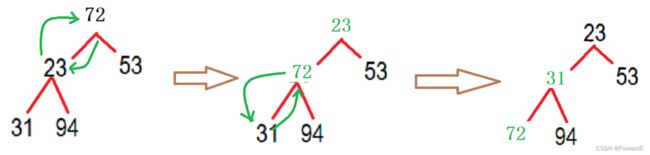
调整的整体原则是：

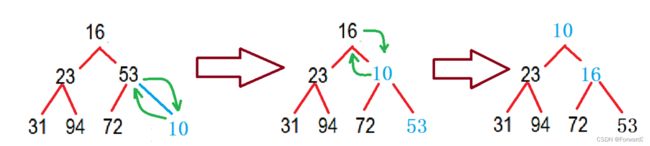
如果原来是小堆：将堆顶数据和左右孩子较小的那一个比较，如果堆顶数据大于较小值，那么就交换这两个数的位置。继续向下调整，直到满足堆的条件

大堆同理。

如图：

4.2.2 AdjustDown实现（大堆）

void AdjustDown(HPDataType* a, int parent, int n)
{
    //先默认较大的孩子为左孩子
	int child = parent * 2 + 1;

	while (child < n)
	{
        //如果右孩子存在并且右孩子大于左孩子
        //那么较大的孩子应该是右孩子
		if (child + 1 < n && a[child + 1] > a[child])
			child = child + 1;

		//如果父亲小于孩子，那就交换父亲和孩子
        //并继续向下调整
        if (a[parent] < a[child])
		{
			Swap(&a[parent], &a[child]);

			parent = child;
			child = child * 2 + 1;
		}
        //否则已经满足堆的条件，退出循环
		else
			break;
	}
}

4.2.3 HeapPop实现

和插入类似，只要每删除一次数据就进行一次向下调整，就可以保证HeapPop的正确了：

void HeapPop(Heap* hp)
{
    //交换堆顶元素和数组最后一个元素
	Swap(&(hp->a[0]), &(hp->a[hp->size - 1]));

    //更新大小
	hp->size--;

    //向下调整
	AdjustDown(hp->a, 0, hp->size);
}

4.2.4 时间复杂度

和向上调整一样，对于每一次删除，向下调整最多调整高度次，因此时间复杂度为O(logN)

4.3 堆的构建

应该清楚，执行堆的插入和删除之前，堆已经被建立。换一句话说，如果任意给一组数据，同时要对其进行堆的插入删除操作，首先就要确保这一组数据是堆。因此掌握如何建堆是十分重要的。

有两种方式建堆：

4.3.1 向上调整建堆

实现堆的插入时，我们用向上调整的方式来建堆。同样，对于任意一个给定的数组，我们也可以用类似“插入”的方法来建堆。

具体方法（以建大堆为例）：

• 遍历数组
• 数组首元素可以默认为一个大堆
• 从第二个元素开始遍历，可以看作每遍历一个数据，就将这个数据HeapPush到堆中
• 直到遍历完整个数组

for (int i = 1; i < n; i++)
    AdjustUp(hp->a, i);

• 时间复杂度：O(NlogN)

4.3.2 向下调整建堆

也可以采用分治的思想：如果构成二叉树的所有子树都是堆，那么这棵二叉树也就一定是堆。

那么我们就可以从最后一棵子树开始，用向下调整的方法建堆：

具体方法：

• 最后一个元素的下标为size - 1，其对应父亲parent的下标为(size - 1 - 1)/2
• 从parent开始向前遍历数组，对每一棵子树进行向下调整
• 直到遍历完整个数组

int parent = (hp->size - 1 - 1) / 2;
while (parent >= 0)
{
    AdjustDown(hp->a, parent, hp->size);

    parent--;
}

• 时间复杂度：O(N)

---

5. 堆的应用

堆的主要用途有堆排序和处理TopK问题，感兴趣的小伙伴可以点击下面的链接进行进一步了解：

堆排序

TopK问题