C#递归使用及八皇后问题
递归简单使用(寻找路径)
题目描述
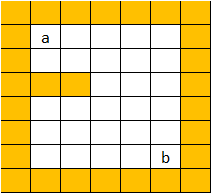
如图所示的地图,有颜色的区域代表有墙体,无法通过,现需要从a点到达b点,通过递归来查找可行路径
代码
using System;
namespace MazeExample
{
class Program
{
static void Main(string[] args)
{
//创建一个二维数组模拟迷宫
int[,] map = new int[8, 7];
//使用 1 表示墙
for (int i = 0; i < 7; i++)
{
map[0, i] = 1;
map[7, i] = 1;
}
for (int i = 0; i < 8; i++)
{
map[i, 0] = 1;
map[i, 6] = 1;
}
map[3, 1] = 1;
map[3, 2] = 1;
//map[1, 2] = 1;
//map[2, 2] = 1;
//输出地图
for (int i = 0; i < 8; i++)
{
for (int j = 0; j < 7; j++)
{
Console.Write(map[i, j] + " ");
}
Console.WriteLine();
}
bool tag = SetWayByAnotherStrategy(map, 1, 1);
//输出新地图
for (int i = 0; i < 3; i++)
{
Console.WriteLine();
}
for (int i = 0; i < 8; i++)
{
for (int j = 0; j < 7; j++)
{
Console.Write(map[i, j] + " ");
}
Console.WriteLine();
}
}
/*
* 1.map表示地图
* 2.i,j表示从地图的哪个位置开始找
* 3.如果小球能到达map[6,5]的位置,则说明通路找到
* 4.约定 当map[i,j]为0表示该点没有走过, 1表示墙, 3表示通路可以走, 3表示该点已经走过,但是走不通
* 5.走迷宫时,需要确定一个策略,下->右->上->左,如果该点走不通,再回溯
*/
/// 如果找到通路,就返回ture,否则返回false
static bool SetWay(int[,]map,int i, int j)
{
if (map[6,5] == 2) //退出条件
{
return true;
}
else
{
//如果当前这个点还没有走过
if (map[i,j] == 0)
{
//按照策略走 下->右->上->左
map[i, j] = 2; //假定该点可以走通
if (SetWay(map,i+1,j)) //向下走
{
return true;
}
else if(SetWay(map,i,j+1))
{
return true;
}
else if(SetWay(map,i-1,j))
{
return true;
}
else if (SetWay(map,i,j-1))
{
return true;
}
else
{
//说明该点走不通
map[i, j] = 3;
return false;
}
}
else
{
//如果 map[i,j] != 0 则可能是1、2、3
return false;
}
}
}
//修改策略 上->右->上->左
static bool SetWayByAnotherStrategy(int[,] map, int i, int j)
{
if (map[6, 5] == 2) //退出条件
{
return true;
}
else
{
//如果当前这个点还没有走过
if (map[i, j] == 0)
{
//按照策略走 下->右->上->左
map[i, j] = 2; //假定该点可以走通
if (SetWayByAnotherStrategy(map, i-1, j)) //向下走
{
return true;
}
else if (SetWayByAnotherStrategy(map, i, j + 1))
{
return true;
}
else if (SetWayByAnotherStrategy(map, i + 1, j))
{
return true;
}
else if (SetWayByAnotherStrategy(map, i, j - 1))
{
return true;
}
else
{
//说明该点走不通
map[i, j] = 3;
return false;
}
}
else
{
//如果 map[i,j] != 0 则可能是1、2、3
return false;
}
}
}
}
}
八皇后问题
题目描述
一个8×8的棋盘,将八个皇后摆放在棋盘上,各个皇后之间不能在同一行、同一列、同一斜线上,试求所有可能的解法
思路
- 将第一个皇后放在第一行第一列
- 第二个皇后放在第二行第二列,判断是否可行,如果不可行则依次遍历第二列、第三列 … 直到把所有列放一遍
- 继续第三个皇后、第四个皇后,直到第8个皇后也能放在一个不冲突的位置,即找到了一个正确解。
[注] 代码使用一维数组来模拟棋盘 下标代表放置的行数,对应的值代表放置的列数。 例如 arr[i] = val 则说明 第 i+1 个皇后放在第 i+1 行的第 val 列。
代码
using System;
namespace EightQueenProblem
{
class Program
{
//定义一个max表示一共有多少个皇后
static int max = 8;
static int cnt = 0; //解法的数量
//定义一个数组用于保存皇后放置的结果, 比如 arr = {0,4,7,5,2,6,1,3}
static int[] array = new int[max];
static void Main(string[] args)
{
Check(0);
Console.WriteLine(cnt);
}
//放置第n个皇后的方法
static void Check(int n)
{
if (n == max) //8个皇后已经放好了
{
cnt++;
Print();
Console.WriteLine();
return;
}
//依次放入皇后并判断是否冲突
for (int i = 0; i < max; i++)
{
//先把当前这个皇后 n, 放在该行的第一列
array[n] = i;
//判断当放置第n个皇后到i列时是否冲突
if (Judge(n)) //不冲突
{
//接着放第n+1个皇后
Check(n + 1);
}
//如果冲突,继续执行for循环,array[n]=i; 即把第n个皇后放置在后一列
}
}
//写一个方法,打印摆放的位置
static void Print()
{
for (int i = 0; i < array.Length; i++)
{
Console.Write(array[i] + " ");
}
Console.WriteLine();
}
//查看当放置第n个皇后时,检测该皇后是否与之前已经存在的皇后冲突
///