AtCoder Beginner Contest 223(A,B,C,D,E,G)题解

A - Exact Price

题意：

你钱包里有一张或更多的$100$块，问你钱包里钱的总数会不会是$x$。

思路：

判断$x$是不是$100$的倍数，以及特判$0$。

代码：

#include
#define fi first
#define se second
#define ll long long
#define mp make_pair
#define pb push_back
#define ls x<<1
#define rs x<<1|1
#define lson x<<1,l,mid
#define rson x<<1|1,mid+1,r
#define pii pair<int,int>
#define all(x) x.begin(),x.end()
#define cl(x,y) memset(x,y,sizeof(x))
#define nxtp(a,n) next_permutation(a+1,a+n+1)
#define mem(x,y,n) memset(x,y,sizeof(int)*(n+5))
const int N=1e6+10;
const int mod=1e9+7;
const int inf=0x3f3f3f3f;
const double eps=1e-8;
const double pi=acos(-1);
const double INF=1e18;
using namespace std;
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	int n;
	cin>>n;
	cout<<(n%100==0 && n?"Yes":"No")<<endl;
	return 0;
}

B - String Shifting

题意：

给一个字符串$s$，可以将一个前缀移到字符串尾部，一个后缀移到字符串头部，可以操作任意次。问字典序最大最小的情况。

思路：

发现两种操作其实本质上相同，一共只有$n$种。把所有的情况存起来，即跑$n$次，每次将$s$的第一个字符移到最后变成新的$s$。然后排序，取字典序最大和最小即可。

代码：

#include
#define fi first
#define se second
#define ll long long
#define mp make_pair
#define pb push_back
#define ls x<<1
#define rs x<<1|1
#define lson x<<1,l,mid
#define rson x<<1|1,mid+1,r
#define pii pair<int,int>
#define all(x) x.begin(),x.end()
#define cl(x,y) memset(x,y,sizeof(x))
#define nxtp(a,n) next_permutation(a+1,a+n+1)
#define mem(x,y,n) memset(x,y,sizeof(int)*(n+5))
const int N=1e6+10;
const int mod=1e9+7;
const int inf=0x3f3f3f3f;
const double eps=1e-8;
const double pi=acos(-1);
const double INF=1e18;
using namespace std;
string s;
vector<string> a;
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>s;
	int n=s.length(),i;
	for(i=0;i<n;i++)
	{
		a.pb(s);
		s=s+s[0];
		s=s.erase(0,1);
	}
	sort(all(a));
	cout<<a[0]<<endl<<a[n-1]<<endl;
	return 0;
}

C - Doukasen

题意：

给你$n$个木棍，每个木棍长$a_i$，燃烧时间为$b_i$。从$1$到$n$连起来，从两头点燃，问烧尽的时候距离左边多远。

思路：

总共燃烧的时间需要$t=\sum _{i=1}^n\frac{a_i}{b_i}$，除以$2$之后就是相遇的时间，然后从头枚举每一个木棍燃烧多长即可。

代码：

#include
#define fi first
#define se second
#define ll long long
#define mp make_pair
#define pb push_back
#define ls x<<1
#define rs x<<1|1
#define lson x<<1,l,mid
#define rson x<<1|1,mid+1,r
#define pii pair<int,int>
#define all(x) x.begin(),x.end()
#define cl(x,y) memset(x,y,sizeof(x))
#define nxtp(a,n) next_permutation(a+1,a+n+1)
#define mem(x,y,n) memset(x,y,sizeof(int)*(n+5))
const int N=1e6+10;
const int mod=1e9+7;
const int inf=0x3f3f3f3f;
const double eps=1e-8;
const double pi=acos(-1);
const double INF=1e18;
using namespace std;
int a[N],b[N];
int main()
{
	int n,i;
	double t;
	scanf("%d",&n);
	for(i=1;i<=n;i++)
	{
		scanf("%d%d",&a[i],&b[i]);
		t+=a[i]*1.0/b[i];
	}
	t/=2;
	double len=0;
	for(i=1;i<=n;i++)
	{
		double v=min(t,a[i]*1.0/b[i]);
		len+=v*b[i];
		t-=v;
	}
	printf("%.15lf\n",len);
	return 0;
}

D - Restricted Permutation

题意：

构造一个长度为$n$的排列，满足$m$个约束：数字$a_i$出现在$b_i$之前。并且排列字典序最小。不能则输出“-1”。

思路：

拓扑排序，$a_i$向$b_i$连边。因为要字典序最小，所以通过优先队列维护。-1的情况就是存在环，就是没有访问到$n$个点，就是答案数组大小小于$n$。

代码：

#include
#define fi first
#define se second
#define ll long long
#define mp make_pair
#define pb push_back
#define ls x<<1
#define rs x<<1|1
#define lson x<<1,l,mid
#define rson x<<1|1,mid+1,r
#define pii pair<int,int>
#define all(x) x.begin(),x.end()
#define cl(x,y) memset(x,y,sizeof(x))
#define nxtp(a,n) next_permutation(a+1,a+n+1)
#define mem(x,y,n) memset(x,y,sizeof(int)*(n+5))
const int N=1e6+10;
const int mod=1e9+7;
const int inf=0x3f3f3f3f;
const double eps=1e-8;
const double pi=acos(-1);
const double INF=1e18;
using namespace std;
vector<int> e[N];
int d[N],a[N];
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	int n,m,i;
	cin>>n>>m;
	for(i=1;i<=m;i++)
	{
		int u,v;
		cin>>u>>v;
		e[u].pb(v);
		d[v]++;
	}
	int len=0;
	priority_queue<int,vector<int>,greater<int>>q;
	for(i=1;i<=n;i++)
		if(d[i]==0)
			q.push(i);
	while(!q.empty())
	{
		int u=q.top();
		q.pop();
		a[++len]=u;
		for(auto v:e[u])
		{
			d[v]--;
			if(d[v]==0)
				q.push(v);
		}
	}
	if(len!=n)
		cout<<-1<<endl;
	else
		for(i=1;i<=n;i++)
			cout<<a[i]<<" ";
	return 0;
}

E - Placing Rectangles

题意：

一个大小为$X\times Y$的长方形中，是否能放下面积至少为$A,B,C$的三个长方形。

思路：

贪心的想，尽量放的长方形的面积要尽可能接近$A,B,C$。
再考虑放的形状只会存在如下四种：

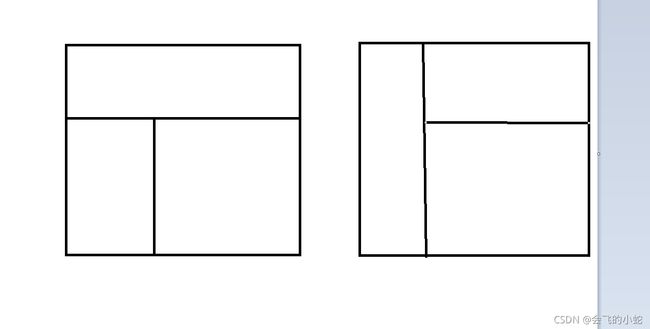
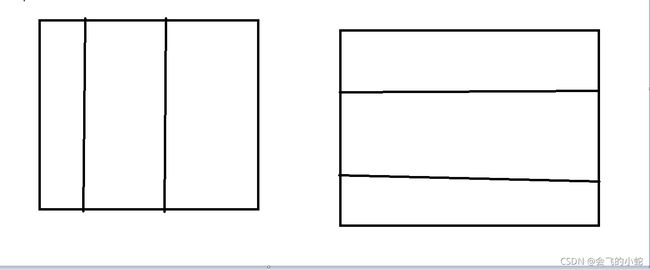
对于第一类情况，上面（左边）需要枚举放$A,B,C$三种情况是否成立。
也就是枚举八种情况，看看存不存在一种情况成立。可以将一些情况稍微合并一下减少代码量。

代码：

#include
#define fi first
#define se second
#define int long long
#define mp make_pair
#define pb push_back
#define ls x<<1
#define rs x<<1|1
#define lson x<<1,l,mid
#define rson x<<1|1,mid+1,r
#define pii pair<int,int>
#define all(x) x.begin(),x.end()
#define cl(x,y) memset(x,y,sizeof(x))
#define nxtp(a,n) next_permutation(a+1,a+n+1)
#define mem(x,y,n) memset(x,y,sizeof(int)*(n+5))
const int N=1e6+10;
const int mod=1e9+7;
const int inf=0x3f3f3f3f;
const double eps=1e-8;
const double pi=acos(-1);
const double INF=1e18;
using namespace std;
int x,y,a[10];
int check1()
{
	int sum=0,i;
	for(i=1;i<=3;i++)
		sum+=(a[i]+x-1)/x;
	return sum<=y;
}
int check2(int p)
{
	int v=x;
	v-=(a[p]+y-1)/y;
	if(v<=0)
		return 0;
	int sum=0,i;
	for(i=1;i<=3;i++)
		if(p!=i)
			sum+=(a[i]+v-1)/v;
	return sum<=y;
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>x>>y;
	int i;
	for(i=1;i<=3;i++)
		cin>>a[i];
	int f=0;
	f|=check1();
	for(i=1;i<=3;i++)
		f|=check2(i);
	swap(x,y);
	f|=check1();
	for(i=1;i<=3;i++)
		f|=check2(i);
	cout<<(f?"Yes":"No")<<endl;
	return 0;
}

G - Vertex Deletion

题意：

一个$n$个结点的树，求符合要求的结点个数：删掉结点$i$后的最大匹配数和原来树的最大匹配数相等。

思路：

先思考什么样的点才能成为符合要求的点，就是删了这个点之后，与他匹配的点能和其他的点匹配。换言之，这个点通过增广路能够再找到一个非匹配点。这就类似于二分图博弈中找必胜点了。

代码：

#include
#define pii pair<int,int>
#define pb push_back
#define int long long
#define cl(x,y) memset(x,y,sizeof(x))
#define ct cerr<<"Time elapsed:"<<1.0*clock()/CLOCKS_PER_SEC<<"s.\n";
const int N=5e5+210;
const int mod=1e9+7;
const int maxn=0x3f3f3f3f;
const int minn=0xc0c0c0c0;
const int inf=99999999;
using namespace std;
struct edge
{
	int u,v,w;
}maze[N<<1];
int len=1,head[N]={0};
int dep[N],n,m,s,t;//深度 
vector<int> e[N];
void add(int u,int v,int w)
{
	maze[++len]={head[u],v,w};
	head[u]=len;
}
void inc(int u,int v,int w)
{
	add(u,v,w);
	add(v,u,0);
}
int dfs(int u,int f,int t)
{
	int ans=0,i;
	if(u==t)
		return f;
	for(i=head[u];i && f;i=maze[i].u)
	{
		int v=maze[i].v,w=maze[i].w;
		if(dep[v]==dep[u]+1 && w)//符合深度关系且能流 
		{
			int sum=dfs(v,min(f,w),t);
			maze[i].w-=sum;
			maze[i^1].w+=sum;
			f-=sum;
			ans+=sum;
		}	
	}
	if(!ans)
		dep[u]=-2;
	return ans;
}
int bfs(int s,int t)
{
	int i;
	queue<int> q;
	for(i=s;i<=t;i++)
		dep[i]=0;
	dep[s]=1;//源点深度为1
	q.push(s);
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(i=head[u];i;i=maze[i].u)
		{
			int v=maze[i].v,w=maze[i].w;
			if(w && !dep[v])//有深度且能流 
			{
				dep[v]=dep[u]+1;
				q.push(v); 
			}
		}
	}
	return dep[t];
}
int dinic(int s,int t)
{
	int ans=0;
	while(bfs(s,t))
	{
		ans+=dfs(s,maxn,t);
		//pcout<
	}
	return ans;
}
int col[N],vis[N],cho[N];
void find(int x,int lim)
{
	int i;
	if(vis[x])
		return;
	vis[x]=1;
	if(col[x]==lim)
		cho[x]=1;
	for(i=head[x];i;i=maze[i].u)
	{
		if(maze[i].w==lim)
			find(maze[i].v,lim);
	}
}
void color(int u,int co,int fa)
{
	col[u]=co;
	if(co)
		inc(s,u,1);
	else
		inc(u,t,1);
	for(auto v:e[u])
	{
		
		if(co)	
			inc(u,v,1);
		if(v==fa)
			continue;
		color(v,co^1,u);
	}
	return;
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	int n,i;
	cin>>n;
	for(i=1;i<n;i++)
	{
		int u,v;
		cin>>u>>v;
		e[u].pb(v);
		e[v].pb(u);
	}
	s=0;
	t=n+1;
	color(1,0,0);
	int maxflow=dinic(s,t);
	int sum=0;
	find(s,1);
	cl(vis,0);
	find(t,0);
	int ans=0;
	for(i=1;i<=n;i++)
		if(cho[i])
			ans++;
	cout<<ans<<endl;
	return 0;
}