线性回归网络

  李沐大神的《动手学深度学习》，是我入门机器学习的首课，因此在这里记录一下学习的过程。

线性回归的从零开始实现

  线性回归是理解机器学习的基础，它经常用来表示输入和输出之间的关系。
  线性回归基于几个简单的假设： 首先，假设自变量X和因变量y之间的关系是线性的， 即y可以表示为X中元素的加权和，这里通常允许包含观测值的一些噪声。

  下面基于房屋价格price和房屋的面积area与年龄age之间的关系来构造出了一个线性模型

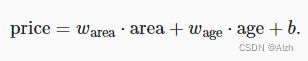
  $w_{area}$和$w_{age}$称为权重（weight），权重决定了每个特征对我们预测值的影响。$b$称为偏置（bias）、偏移量（offset）或截距（intercept）。 偏置是指当所有特征都取值为0时，预测值应该为多少。

  基于如上的线性模型从零开始实现一个线性回归模型的示例代码
代码如下：

import random
import torch
from d2l import torch as d2l

# 生成合成数据集
def synthetic_data(w, b, num_examples):  #@save
    """生成y=Xw+b+噪声"""
    # 生成均值为0，标准差为1的随机数，形状为num_examples行len(w)列
    X = torch.normal(0, 1, (num_examples, len(w)))
    # matmul为两个张量的矩阵乘积
    y = torch.matmul(X, w) + b
    # 加上随机噪音
    y += torch.normal(0, 0.01, y.shape)
    # y作为列向量返回,x
    return X, y.reshape((-1, 1))

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)
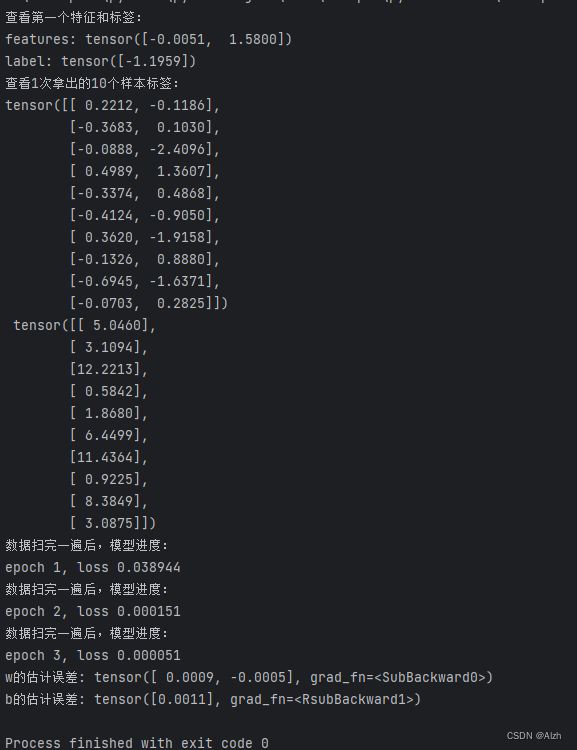
print('查看第一个特征和标签：')
print('features:', features[0],'\nlabel:', labels[0])

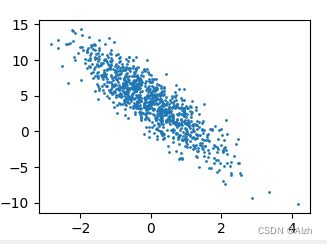
d2l.set_figsize()
d2l.plt.scatter(features[:, 1].detach().numpy(), labels.detach().numpy(), 1)
d2l.plt.show()

# 读取数据集
def data_iter(batch_size, features, labels):
    num_examples = len(features)
    # 生成每个样本的下标
    indices = list(range(num_examples))
    # 这些样本是随机读取的，没有特定的顺序（将下标打乱）
    random.shuffle(indices)
    for i in range(0, num_examples, batch_size):
        # 拿出batch_size个下标
        batch_indices = torch.tensor(
            indices[i: min(i + batch_size, num_examples)])
        # 拿出batch_size个随机的特征和标签
        yield features[batch_indices], labels[batch_indices]

batch_size = 10
print('查看1次拿出的10个样本标签：')
for X, y in data_iter(batch_size, features, labels):
    print(X, '\n', y)
    break

# 生成均值为0，标准差为0.01的随机数，形状为2行1列，需要计算梯度
w = torch.normal(0, 0.01, size=(2,1), requires_grad=True)
# 返回一个全为标量 0 的张量，形状由可变参数sizes 定义，需要计算梯度
b = torch.zeros(1, requires_grad=True)

# 定义模型
def linreg(X, w, b):  #@save
    """线性回归模型"""
    return torch.matmul(X, w) + b

# 定义损失函数
# y_hat为预测值，y为真实值
def squared_loss(y_hat, y):  #@save
    """均方损失"""
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2

# 定义优化算法
def sgd(params, lr, batch_size):  #@save
    """小批量随机梯度下降"""
    # 更新的时候不需要反向传播（进行梯度计算）
    with torch.no_grad():
        for param in params:
            # 此处/batch_size是因为下面计算了l.sum()
            param -= lr * param.grad / batch_size
            # 将梯度设为0
            param.grad.zero_()

# 学习率
lr = 0.03
# 数据扫描次数
num_epochs = 3
# 模型
net = linreg
# 损失函数
loss = squared_loss

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y)  # X和y的小批量损失
        # 因为l形状是(batch_size,1)，而不是一个标量。l中的所有元素被加到一起，
        # 并以此计算关于[w,b]的梯度
        l.sum().backward()
        sgd([w, b], lr, batch_size)  # 使用参数的梯度更新参数
    # 数据扫完一遍后，评价一下模型进度
    with torch.no_grad():
        train_l = loss(net(features, w, b), labels)
        print('数据扫完一遍后，模型进度：')
        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')

print(f'w的估计误差: {true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差: {true_b - b}')

生成的随机数据如下：

代码运行结果如下：

线性回归的简洁实现

  简洁实现相对来说只是可以使用一些封装好的函数，底层逻辑还是一样的。
代码如下：

import torch
from torch.utils import data
from d2l import torch as d2l


# 生成数据集
true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)

# 读取数据集
# 该函数使用 PyTorch 的 data.TensorDataset 类将输入数据和标签数据封装为一个矩阵。然后使用 PyTorch 的 data.DataLoader 类将 TensorDataset 对象作为数据源，并设置批次大小和是否打乱数据。
def load_array(data_arrays, batch_size, is_train=True):  #@save
    """构造一个PyTorch数据迭代器"""
    # 将数据和标签封装为一个 TensorDataset 对象
    dataset = data.TensorDataset(*data_arrays)
    # 返回一个 DataLoader 对象，使用 DataLoader 对象返回一个数据加载器，可以通过它对数据进行迭代。最后返回一个数据迭代器。
    return data.DataLoader(dataset, batch_size, shuffle=is_train)

batch_size = 10
data_iter = load_array((features, labels), batch_size)

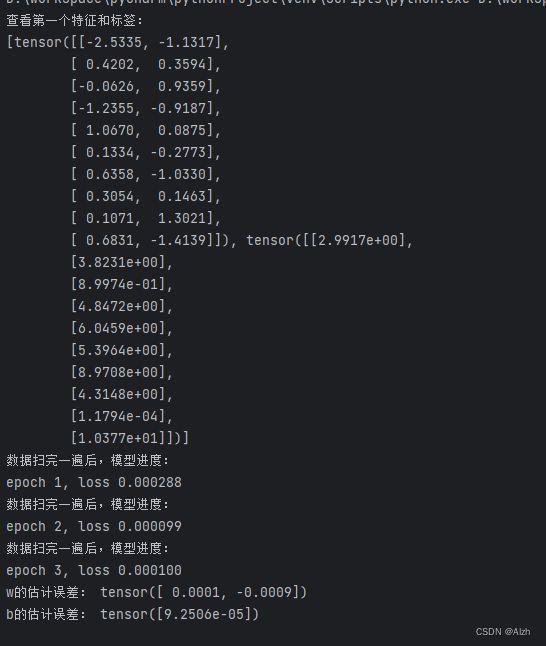
print('查看第一个特征和标签：')
# 使用iter构造Python迭代器，并使用next从迭代器中获取第一项
print(next(iter(data_iter)))

# nn是神经网络的缩写
from torch import nn
# 定义模型
# nn.Linear(2, 1) 表示创建一个线性层，输入特征维度为 2，输出特征维度为 1。输入维度为 2，意味着在训练模型时需要提供一个 2 维的特征向量作为输入。它将输入的 2 维特征通过线性变换映射到一个 1 维输出值。
net = nn.Sequential(nn.Linear(2, 1))

# 初始化模型参数
# 通过net[0]选择网络中的第一个图层， 然后使用weight.data和bias.data方法访问参数
# weight.data 表示该层的权重参数，bias.data 表示该层的偏置参数。
# 使用 normal_() 方法对权重参数进行随机初始化，参数分布服从均值为 0、标准差为 0.01 的正态分布。
# 使用 fill_() 方法对偏置参数进行初始化，将偏置值设置为 0。
net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)

# 定义损失函数
# 计算均方误差使用的是MSELoss类，也称为平方L2范数。 默认情况下，它返回所有样本损失的平均值。
loss = nn.MSELoss()

# 定义优化算法
trainer = torch.optim.SGD(net.parameters(), lr=0.03)

# 训练
num_epochs = 3
for epoch in range(num_epochs):
    for X, y in data_iter:
        # 计算平均损失值
        l = loss(net(X) ,y)
        # 清零模型的梯度，以确保每次迭代前梯度的正确计算
        trainer.zero_grad()
        # 计算损失函数关于模型参数的梯度
        l.backward()
        # 更新模型的参数
        trainer.step()
    # 计算整个训练集的损失值l，并打印出当前轮数和对应的损失值
    l = loss(net(features), labels)
    print('数据扫完一遍后，模型进度：')
    print(f'epoch {epoch + 1}, loss {l:f}')

w = net[0].weight.data
print('w的估计误差：', true_w - w.reshape(true_w.shape))
b = net[0].bias.data
print('b的估计误差：', true_b - b)

代码运行结果如下：

总结：
  通过这个代码也算了解了线性回归模型算法的基本步骤，目前这个代码是懂了，但是还无法真正自己实现一个，先慢慢理解，多回顾。