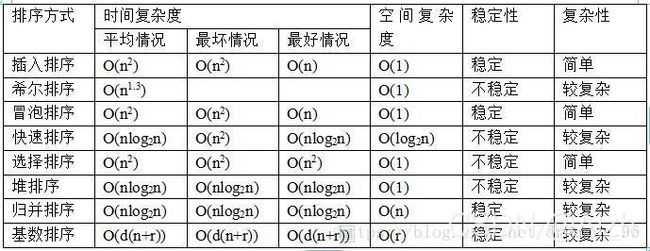
常见排序算法学习

由于面试的时候排序算法是基础中的基础，所以特来总结一波排序算法的知识。

冒泡排序

思想：一开始交换的区间为 0~n-1，从0位置开始前后两个数比较，大的放在后面，这样依次交换下去，最大的数会最终放在数组的最后。然后范围变为0~n-2，从0位置开始比较交换，这样最终第二大的数会放在数组的倒数第二个位置。… 然后依次进行这样的交换过程，当区间只剩下一个数的时候，整个数组就变得有序了。

代码：

#include
using namespace std;

const int maxn=1e5+5;
int a[maxn];
int n;

void maoPaoSort()
{
    for(int i=0;ia[j+1])
            {
                int tmp=a[j];
                a[j]=a[j+1];
                a[j+1]=tmp;
            }
        }
    }
}

int main()
{
    scanf("%d",&n);
    for(int i=0;i

选择排序

思想：一开始在数组的整个区间0~n-1上选出一个最小值，把它放到位置0上，然后在区间1~n-1上选出一个最小值，把它放到位置1上。这样依次操作，直到最后范围中只包含一个数的时候，整个数组就变得有序了。

插入排序

思想：首先是位置1上的数与位置0上的数进行比较，如果位置1上的数更小，那么它就与位置0上的数进行交换。接下来考察位置2上的数记为a，如果a比位置1上的数小，那它就与位置1上的数进行交换，接着再与位置0上的数进行比较，如果它还是更小就与位置0上的数进行交换。接下来，对于位置k上的数，假设它的值记为b，b就依次和前面位置上的数进行比较，如果b一直小于前面的数，那么它一直进行这样的交换过程，直到前面的数<=b，那么b就插入当前位置。那么依次从1位置到n-1位置，所有的数都进行了这样比较、插入的过程，最终整个数组就变得有序了。

快速排序

思想： 随机地在数组中选择一个数（通常选第一个数），<=它的数统一放在这个数的左边，>它的数统一放在这个数的右边，接下来对左右两个数组递归地调用快速排序的过程，这样整个数组最终就会有序了。
划分过程：首先，将划分值放在整个数组的最后位置，然后我们设置一个<=区间，在初始的时候，<=区间的长度为0，放在整个数组的左边，接下来从左到右遍历所有元素，如果当前元素>划分值，那么就继续遍历下一个元素，如果当前元素<=划分值，就把当前数和<=区间的下一个数交换，并且让<=区间向右扩一个位置，那么在遍历完所有的元素，直到划分值的时候，将划分值与<=区间的下一个元素进行交换，这个就是一次完整的划分过程。
代码：

#include
using namespace std;

const int maxn=1e5+5;
int a[maxn];

void QuickSort(int *pArray, int iBegin, int iEnd)
{
    if (iBegin < iEnd)
    {
        int iLeft = iBegin;
        int iRight = iEnd;
        int iPivot = pArray[iBegin];

        while (iLeft < iRight)
        {
            while (iLeft < iRight && pArray[iRight] >= iPivot)
                --iRight;
            if(iLeft < iRight)
                pArray[iLeft++] = pArray[iRight];

            while (iLeft < iRight && pArray[iLeft] <= iPivot)
                ++iLeft;
            if(iLeft < iRight)
                pArray[iRight--] = pArray[iLeft];
        }
        pArray[iLeft] = iPivot;
        QuickSort(pArray, iBegin, iLeft - 1);
        QuickSort(pArray, iRight + 1, iEnd);
    }
}

int main()
{
    int n;
    scanf("%d",&n);
    for(int i=0; i

总共有三种实现的方法，(这里仅给出一种代码)

1. 左右指针法
   核心思想：从left一直向后走，直到找到一个大于key的值，right从后至前，直至找到一个小于key的值，然后交换这两个数
2. 挖坑法
   核心思想：从left一直向后走，直到找到一个大于key的值，然后将该数放入坑中，坑位变成了array[left]。然后right一直向前走，直到找到一个小于key的值，然后将该数放入坑中，坑位变成了array[right]。
3. 前后指针法
   核心思想：在没找到大于key值之前，small永远紧跟index，遇到大的两者之间就会拉开差距，中间差的肯定是连续的大于key的值，当再次遇到小于key的值时，交换两个下标对应的值就好了。

总结：
左右指针法是最常用的方法，而前后指针法比较绕，但是它是单向扫描的，所以如果待排序的序列是单向链表的话，就可以用前后指针法。

快速排序的优化
首先快排的思想是找一个枢轴，然后以枢轴为中介线，一边都小于它，另一边都大于它，然后对两段区间继续划分，那么枢轴的选取就很关键。
1、三数取中法
上面的代码思想都是直接拿序列的最后一个值作为枢轴，如果最后这个值刚好是整段序列最大或者最小的值，那么这次划分就是没意义的。
所以当序列是正序或者逆序时，每次选到的枢轴都是没有起到划分的作用。快排的效率会极速退化。

所以可以每次在选枢轴时，在序列的第一，中间，最后三个值里面选一个中间值出来作为枢轴，保证每次划分接近均等。

2、直接插入
由于是递归程序，每一次递归都要开辟栈帧，当递归到序列里的值不是很多时，我们可以采用直接插入排序来完成，从而避免这些栈帧的消耗。

非递归实现快排
主要思想就是用栈来保存区间。

归并排序

思想：首先让数组中的每一个数单独成为长度为1的有序区间，然后把相邻的长度为1的有序区间进行合并，得到最大长度为2的有序区间，接下来再把相邻的有序区间进行合并，得到最大长度为4的有序区间。依次这样进行下去，4合8,8合16，直到数组中所有的数组成一个统一的有序区间，就结束了。
代码：

#include
using namespace std;

const int maxn=1e5+5;
int a[maxn];
int tmp[maxn];

void mergeArray(int *p,int le,int mid,int ri)
{
    int k=le;
    int i=le;
    int j=mid+1;
    while(i<=mid&&j<=ri)
    {
        if(a[i]>1;
        mergeSort(p,le,mid);
        mergeSort(p,mid+1,ri);
        mergeArray(p,le,mid,ri);
    }
}


int main()
{
    int n;
    scanf("%d",&n);
    for(int i=0; i

堆排序

思想：首先将数组中的n个数建成一个大小为n的大根堆，堆顶是所有元素的最大值，将堆顶元素和堆的最后一个位置上的元素进行交换，然后把最大值脱离出整个堆结构，放在数组的最后位置，作为数组的有序部分存下来。接下来再把n-1大小的堆从堆顶位置开始进行大根堆的调整，再调整出一个n-1个数中的最大值放在堆顶位置，然后把堆顶位置和堆最后一个位置上的数进行交换，同样将这个最大值脱离出来，放在数组的倒数第二位置作为数组的有序部分。接下来继续这样的堆调整取值，这样堆的大小会依次-1，数组的有序部分会依次增加，当堆的大小减为1的情况下，整个数组就变得整体有序了。
代码：

#include
using namespace std;

const int maxn=1e5+5;
int a[maxn];

// 一次排序过程
void heapify(int *p,int currentRootNode,int size)
{
    if(currentRootNodep[maxNode])
                maxNode=left;
        }

        if(rightp[maxNode])
                maxNode=right;
        }

        //如果最大的不是根元素位置，那么就交换
        if(maxNode!=currentRootNode)
        {
            int temp=p[currentRootNode];
            p[currentRootNode]=p[maxNode];
            p[maxNode]=temp;

            //继续比较，直到完成一次建堆
            heapify(p,maxNode,size);
        }

    }
}

// 创建大根堆
void maxHeapify(int *p,int size)
{
    for(int i=size-1;~i;--i)
    {
        heapify(p,i,size);
    }
}

void heapSort(int *p,int size)
{
    // 每次得到一个当前最大值，加入有序数组
    for(int i=0;i

希尔排序

思想：实际上是插入排序的改良算法，插入排序的步长为1，希尔排序的步长是从大到小调整的。

还有计数排序和基数排序，思想都是来源于桶排序。