哈夫曼树与哈夫曼编码

哈夫曼树与哈夫曼编码

哈夫曼树

哈夫曼树又称最优二叉树，这种数据结构主要用于解决一些编码问题，与普通二叉树相比，哈夫曼树在特定场景下能够显著的提高效率。

相关概念

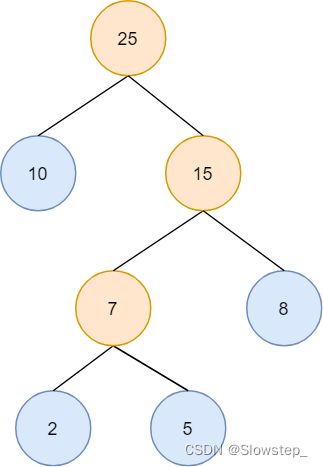
权值：指哈夫曼树叶子节点的权值，例如上图中哈夫曼树树的叶子节点权值为2,5,8,10

路径长度：指从根节点出发，到达叶子节点所经过的边的数目，例如上图中权值为2的节点路径长度为3

树的路径长度：树的路径长度等于这颗树中所有节点的路径长度之和，包括叶子节点和非叶子节点，例如上图中这颗哈夫曼树的路径长度=1+1+2+2+3+3

结点的带权路径长度：结点的带权路径长度等于结点的路径长度×结点的权值，一般认为结点的带权路径长度指的是叶子结点的带权路径长度，例如上图权值为2的结点的带权路径长度=2*3

树的带权路径长度：树的带权路径长度等于这颗哈夫曼树中所有叶子节点的带权路径长度之和，称为WPL(weight path length)

如何构建一颗哈夫曼树？

哈夫曼树要求整个树的WPL值最小，根据WPL的计算规则，在构建哈夫曼树时，需要让权值大的叶子节点靠近根节点，权值小的叶子节点远离根节点。构建哈夫曼树的一般步骤如下：

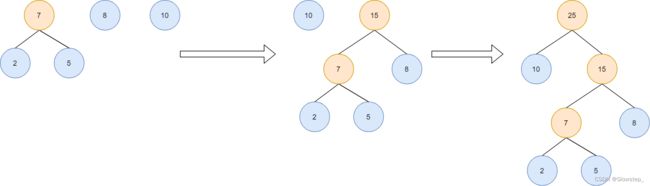
1. 选取权值最小的2个节点进行合并，合并之后的父节点权值=左节点权值+右节点权值(一般权值小的节点在左，权值较大的节点在右)

2. 将父节点与其它叶子节点按照相同的规则进行合并，直到最终只剩下一个节点

3. 以[2,5,8,10]为例说明上述过程

   

C++代码实现：

#define VALUE_INDEX 0
#define LEFT_INDEX 1
#define RIGHT_INDEX 2
#define FATHER_INDEX 3
vector<vector<int>> CreateHuffmanTree(const vector<int>& nodes) {
	int n = nodes.size();
	vector<vector<int>> huffman(2 * n, vector<int>(4));
	auto pairCompare = [](const pair<int, int>& l, const pair<int, int>& r) {
		return l.second > r.second;//小堆
	};
	priority_queue<pair<int, int>, vector<pair<int, int>>, decltype(pairCompare)> heap(pairCompare);
	for (int i = 0; i < n; i++) {
		huffman[i + 1][VALUE_INDEX] = nodes[i];
		heap.push(std::make_pair(i + 1, nodes[i]));
	}
	int index = n + 1;//从n+1下标开始填
	while (index < 2 * n) {
		pair<int, int> x = heap.top();
		heap.pop();
		pair<int, int> y = heap.top();
		heap.pop();
		huffman[x.first][FATHER_INDEX] = index;
		huffman[y.first][FATHER_INDEX] = index;
		huffman[index][VALUE_INDEX] = x.second + y.second;
		huffman[index][LEFT_INDEX] = x.first;
		huffman[index][RIGHT_INDEX] = y.first;
		heap.push(std::make_pair(index, huffman[index][VALUE_INDEX]));
		index++;
	}
	return huffman;
}

说明：

• 参数nodes表示所有给定叶子节点的权值(可以出现重复值)

• 这里使用了二维数组作为整个树的逻辑结构，huffman数组中的每一个元素表示一个节点的信息，数组的下标表示节点的编号，例如huffman[2][VALUE_INDEX]表示编号为2的节点对应的权值，huffman[2][LEFT_INDEX]表示编号为2的节点的左节点编号，huffman[2][RIGHT_INDEX]表示编号为2的节点的右节点编号，huffman[2][FATHER_INDEX]表示编号为2的节点的父节点编号

• 对于任意一颗哈夫曼树，都只有度为0的节点或者度为2的节点，不存在度为1的节点，由于二叉树n=n₀+n₁+n₂，且n₀=n₂+1，所以任意一颗哈夫曼树的节点总数n=2n₀-1，因此二维数组的大小至少开到2n₀-1，但是实际上我们将二维数组的大小开到了2n₀，并且弃用了0号下标，原因如下：

  1. 二维数组在初始化时，所有元素均为0，父节点编号为0可以表示不存在父节点，即这个节点是最终构建出来的哈夫曼树的根节点，左右节点编号为0表示左右节点为空，当前节点为叶子节点
  2. 如果将0号下标进行使用，那么当一个元素的父节点编号为0时，是表示这个节点为根节点？还是说这个节点不是根节点，它的父节点是编号为0的节点？

• 在构建哈夫曼树的过程中，使用了堆，因为我们每一次都需要选择最小的2个节点进行合并，并且这2个节点不能是已经选择过的，如果采用遍历操作，时间复杂度为O(N)，使用堆可以加速这一过程

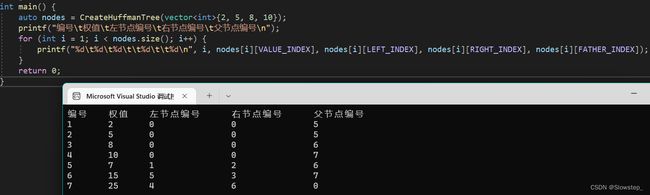
• 使用上述方案，给定叶子节点为[2,5,8,10]，构建出来的哈夫曼树结果如下

  

哈夫曼编码

哈夫曼编码是一种前缀编码，可以将一个字符串编码为一串01序列，编码出来的01序列具有如下特点：

1. 解码方式唯一，不存在任何歧义
2. 对于出现频率高的字符，对应的01序列较短，对于出现频率低的字符，对应的01序列长
3. 通过哈夫曼编码得到的01序列可以保证比大部分其它方式编码得到的01序列短，也就意为着在进行网络传输过程中发送的数据量要更少

前缀编码

使用前缀编码得到的01序列在解码时不会出现歧义，而使用其它编码得到的01序列在进行解码时可能会出现歧义，例如对于"ABC"这个字符串进行编码，规定如下表示方法：

'A' 0
'B' 00
'C' 1

则"ABC"对应的二进制序列为0001，在进行解码时，可以有多种解释，包括"ABC"、“BAC”、“AAAC”，根本原因在于设置编码规则时，'A’对应的编码0为字符’B’对应的编码00的前缀。而以哈夫曼编码为代表的前缀编码就不存在类似问题

生成哈夫曼编码

依然以[2,5,8,10]为例，假设有一个字符串，有2个字符’A’，5个字符’B’，8个字符’C’，10个字符’D’组成，那么生成这个字符串的哈夫曼编码流程如下：

1. 以[2,5,8,10]为权值，构建哈夫曼树

   

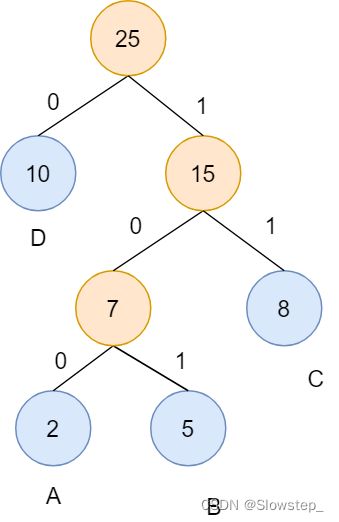
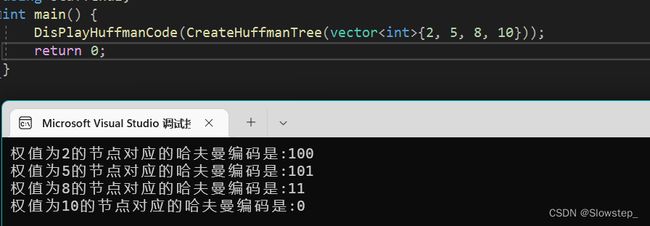
2. 规定向左的边码值为0，向右的边码值为1，那么’D’的哈夫曼编码为0，'A’的哈夫曼编码为100，'B’的哈夫曼编码为101，'C’的哈夫曼编码为11

3. 可以看出，出现频率越高的字符对应的哈夫曼编码越短，并且不存在任意一个字符的编码为另外一个字符的编码前缀，因为这些字符都是对应的叶子节点，因此哈夫曼编码在进行编码与解码时不存在歧义

C++代码实现：

void DisPlayHuffmanCode(const vector<vector<int>>& huffmanTree) {
	int n0 = huffmanTree.size()/2;//叶子节点的个数
	for (int i = 1; i <= n0; i++) {
		string code;
		int cur = i;
		while (huffmanTree[cur][FATHER_INDEX]) {
			int fIndex = huffmanTree[cur][FATHER_INDEX];
			code += huffmanTree[fIndex][LEFT_INDEX] == cur ? '0' : '1';
			cur = fIndex;
		}
		std::reverse(code.begin(), code.end());
		std::cout << "权值为" << huffmanTree[i][VALUE_INDEX] << "的节点对应的哈夫曼编码是:" << code << std::endl;
	}
}

给定权值为[2,5,8,10]，哈夫曼编码结果如下：