平衡二叉树及其算法实现
文章目录
- 1、平衡二叉树
-
- 1.1、什么是二叉搜索树
- 1.2、二叉搜索树的缺点
- 1.3、平衡二叉树的提出
- 1.4、如何构建平衡二叉树(ALV树)
- 1.5 失衡情况及其处理(4种)
-
- 1.5.1 LL——>(右旋)
- 1.5.2 RR——>(左旋)
- 1.5.3 LR——>(先左旋再右旋)
- 1.5.4 RL——>(先右旋再左旋)
- 1.5.5 总结代码实现
- 1.5.6 小结
- 1.5.7 删除结点后该如何调整平衡二叉树?
- 1.6 评价
1、平衡二叉树
1.1、什么是二叉搜索树
1.2、二叉搜索树的缺点
二叉树查找算法查找时间依赖于树的拓扑结构。查找效率取决于树的高度,因此保持树的高度最小,即可保证树的查找效率。最佳情况是 O(log2n),而最坏情况是 O(n)。如果建立的二叉搜索树不平衡了。极端不平衡的情况就是类似一个单链表,这个时候,查找就需要O(n)时间复杂度。
1.3、平衡二叉树的提出
假设我们能够对二叉树进行调正,使得二叉查找树总保持平衡或者不会出现太不平衡的情况。那不就能解决二叉查找树极端情况的出现了从而保证了二叉查找算法的效率了吗。
平衡二叉树的定义
简称平衡二叉树。由前苏联的数学家 Adelse-Velskil 和 Landis 在 1962 年提出的高度平衡的二叉树,根据科学家的英文名也称为 AVL 树。它具有如下几个性质:
平衡因子
定义:某结点的左子树与右子树的高度(深度)差即为该结点的平衡因子(BF,Balance Factor),平衡二叉树中不存在平衡因子大于 1 的节点。在一棵平衡二叉树中,节点的平衡因子只能取 0 、1 或者 -1 ,分别对应着左右子树等高,左子树比较高,右子树比较高。
ALV结构定义
typedef struct AVLNode *Tree;
typedef int ElementType;
struct AVLNode{
int depth; //深度,这里计算每个结点的深度,通过深度的比较可得出是否平衡
Tree parent; //该结点的父节点
ElementType val; //结点值
Tree lchild;
Tree rchild;
AVLNode(int val=0) {
parent = NULL;
depth = 0;
lchild = rchild = NULL;
this->val=val;
}
};
1.4、如何构建平衡二叉树(ALV树)
最小失衡子树:在新插入的结点向上查找,以第一个平衡因子的绝对值超过 1 的结点为根的子树称为最小不平衡子树。也就是说,一棵失衡的树,是有可能有多棵子树同时失衡的。而这个时候,我们只要调整最小的不平衡子树,就能够将不平衡的树调整为平衡的树。
平衡二叉树的失衡调整主要是通过旋转最小失衡子树来实现的。根据旋转的方向有两种处理方式,左旋 与 右旋 。
旋转的目的就是减少高度,通过降低整棵树的高度来平衡。哪边的树高,就把那边的树向上旋转。
1.5 失衡情况及其处理(4种)
ALV树的失衡主要是在插入和删除结点的时候发生的。如:
插入结点:
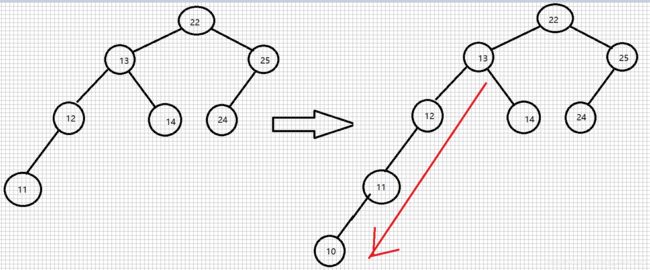
删除结点:
失衡的情况主要有:
A原本是一棵平衡二叉树,现在执行插入操作,可能的情况如表格所示:
| 插入方式 | 描述 | 旋转方式 |
|---|---|---|
| LL | 在 A 的左子树根节点的左子树上插入节点而破坏平衡 | 右旋转 |
| RR | 在 A 的右子树根节点的右子树上插入节点而破坏平衡 | 左旋转 |
| LR | 在A的左子树根节点的右子树上插入节点而破坏平衡 | 先左旋后右旋 |
| RL | 在 A 的右子树根节点的左子树上插入节点而破坏平衡 | 先右旋后左旋 |
1.5.1 LL——>(右旋)
只需要执行一次右旋:(1)将失衡结点A变为其左孩子B的右孩子(2)将其原本的左孩子B的右孩子E变为A的左孩子
1.5.2 RR——>(左旋)

只需要执行一次左旋:(1)将失衡结点A变为其右孩子C的左孩子(2)将其原本的右孩子C的左孩子D变为A的右孩子
1.5.3 LR——>(先左旋再右旋)
若 A 的左孩子节点 B 的右子树 E 插入节点 F ,导致结点 A 失衡,如图:
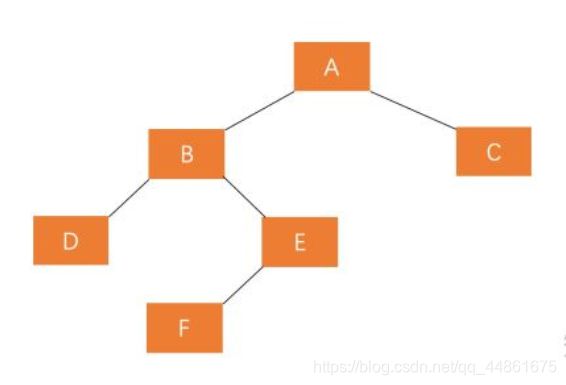
那我们该怎么做呢?先尝试以下右旋:
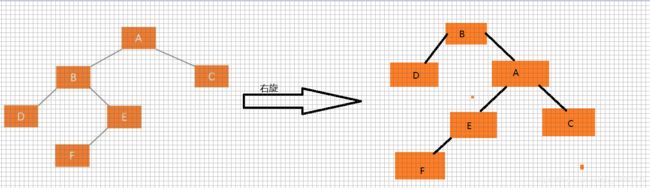
经过右旋调整发现,调整后树仍然失衡,说明这种情况单纯的进行右旋操作不能使树重新平衡。那么这种插入方式需要执行两步操作
- (1)先对失衡节点 A 的左孩子 B 进行左旋操作,即上述 RR 情形操作。
- (2)对失衡节点 A 做右旋操作,即上述 LL 情形操作。
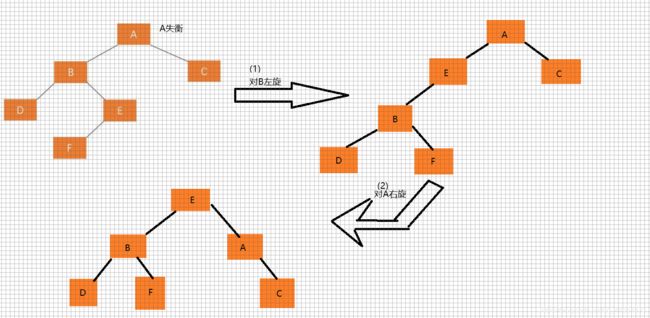
也就是说,经过这两步操作,使得原来根结点的左孩子的右孩子 E 节点成为了新的根节点。
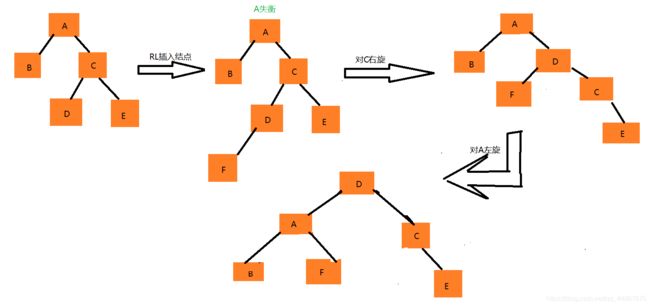
1.5.4 RL——>(先右旋再左旋)
右孩子插入左节点的过程与左孩子插入右节点过程类似,也是需要执行两步操作,使得旋转之后为 原来根结点的右孩子的左孩子作为新的根节点 。(A->D)
1.5.5 总结代码实现
#include1.5.6 小结
在所有的不平衡情况中,都是按照先 寻找最小不平衡树,然后 寻找所属的不平衡类别,再 根据 4 种类别进行固定化程序的操作。
LL , LR ,RR ,RL其实已经为我们提供了最后哪个结点作为新的根指明了方向。如 LR 型最后的根结点为原来的根的左孩子的右孩子,RL 型最后的根结点为原来的根的右孩子的左孩子。只要记住这四种情况,可以很快地推导出所有的情况。
维护平衡二叉树,最麻烦的地方在于平衡因子的维护。
1.5.7 删除结点后该如何调整平衡二叉树?
AVL 树和二叉查找树的删除操作情况一致,都分为四种情况:
+(1)删除叶子节点
+(2)删除的节点只有左子树
+(3)删除的节点只有右子树
+(4)删除的节点既有左子树又有右子树
只不过
AVL 树在删除节点后需要重新检查平衡性并修正,同时,删除操作与插入操作后的平衡修正区别在于,插入操作后只需要对插入栈中的弹出的第一个非平衡节点进行修正,而删除操作需要修正栈中的所有非平衡节点。
删除操作的大致步骤如下:
- 1、 以前三种情况为基础尝试删除节点,并将访问节点入栈。
如果尝试删除成功,则依次检查栈顶节点的平衡状态,遇到非平衡节点,即进行旋转平衡,直到栈空。
如果尝试删除失败,证明是第四种情况。这时先找到被删除节点的右子树最小节点并删除它,将访问节点继续入栈。 - 再依次检查栈顶节点的平衡状态和修正直到栈空。
对于删除操作造成的非平衡状态的修正,可以这样理解:对左或者右子树的删除操作相当于对右或者左子树的插入操作,然后再对应上插入的四种情况选择相应的旋转就好了。
代码实现:
//删除结点
Tree* Delete(Tree *root, const ElenmentType k)
{
if (NULL == root)
return root;
if (!binaryTreeSearch(root,k))//查找删除元素是否存在
{
std::cerr << "Delete error , key not find" << std::endl;
return root;
}
if (k == root->value)//根节点
{
if (root->left!=NULL&&root->right!=NULL)//左右子树都非空
{
if (diff(root) > 0)//左子树更高,在左边删除
{
root->value = tree(root->left,0);//以左子树的最大值替换当前值
root->left = Delete(root->left, root->value);//删除左子树中已经替换上去的节点
}
else//右子树更高,在右边删除
{
root->value = tree(root->right,1);
root->right = Delete(root->right, root->value);
}
}
else//有一个孩子、叶子节点的情况合并
{
Tree * tmp = root;
root = (root->left) ? (root->left) :( root->right);
delete tmp;
tmp = NULL;
}
}
else if (k < root->value)//往左边删除
{
root->left = Delete(root->left, k);//左子树中递归删除
//判断平衡的条件与在插入时情况类似
if (diff(root) < -1)//不满足平衡条件,删除左边的后,右子树变高
{
if (diff(root->right) > 0)
{
root = RL_rotate(root);
}
else
{
root = RR_rotate(root);
}
}
}//end else if
else
{
root->right = Delete(root->right, k);
if (diff(root) > 1)//不满足平衡条件
{
if (diff(root->left) < 0)
{
root = LR_rotate(root);
}
else
{
root = LL_rotate(root);
}
}
}
return root;
}
1.6 评价
平衡二叉树在查找的时候就有二叉查找树的优势,同时也保持了平衡。
但是平衡二叉树的劣势在于:
- 删除:对于平衡二叉树来说,在最坏情况下,需要维护从被删节点到根节点这条路径上所有节点的平衡性,旋转的量级是OlogN。但是红黑树就不一样了,最多只需3次旋转就会重新平衡,旋转的量级是O(1)。
- 保持平衡:平衡二叉树高度平衡,这也就意味着在大量插入和删除节点的场景下,平衡二叉树为了保持平衡需要调整的频率会更高。
所以在大量查找的情况下,平衡二叉树的效率更高,也是首要选择。在大量增删的情况下,红黑树是首选。
最后完整代码:
#include<iostream>
#include<cstdio>
#include<cstdlib>
typedef int ElenmentType;
//平衡二叉树的结构
typedef struct AVLNode{
int depth;//深度
struct AVLNode *left;
struct AVLNode *right;
struct AVLNode *parent;
ElenmentType value;
//构造器
AVLNode(ElenmentType value=0){
parent = NULL;
depth = 0;
left = right = NULL;
this->value=value;
}
}AVLtree,Tree;
//LL型调整函数
//返回根结点
Tree* LL_rotate(Tree *root){//LL执行右旋
//root是原来的平衡二叉树的根结点
Tree *temp;//临时变量
//获取根结点的左孩子
temp = root->left;
//根结点的左孩子变更为其原来左孩子的右孩子
root->left = temp->right;
//原来的根结点的左孩子变为了根结点
temp->right = root;
return temp;
}
//RR型调整函数
//返回根结点
Tree* RR_rotate(Tree * root){//RR执行左旋
Tree* temp;
temp = root->right;//获取根结点的右孩子
root->right = temp->left;//根结点的右孩子变为其原来右孩子的左孩子
temp->left = root;//原来的根结点的右孩子变为了新的根结点
return temp;
}
//1、LR型,先左旋转,再右旋转
//返回:新父节点
Tree* LR_rotate(Tree* root){
Tree* temp;
temp = root->left;
root->left =RR_rotate(temp);
return LL_rotate(root);
}
//2RL型,先右旋转,再左旋转
//返回:新父节点
Tree* RL_rotate(Tree* root){
Tree* temp;
temp = root->right;
root->right=LL_rotate(temp);
return RR_rotate(root);
}
//树高
int height(const Tree* root)//求树高,递归
{
if (root == NULL)
return 0;
return std::max(height(root->left) ,
height(root->right)) + 1;
}
//平衡因子
int diff(const Tree* root)//求平衡因子,即当前节点左右子树的差
{
return height(root->left) - height(root->right);
}
//平衡操作
Tree* Balance(Tree* root)
{
// printf("平衡函数");
int balanceFactor = diff(root);//diff用来计算平衡因子(左右子树高度差)
if (balanceFactor > 1)//左子树高于右子树
{
if (diff(root->left) > 0)//LL的情况
root=LL_rotate(root);
else//LR的情况
root=LR_rotate(root);
}
else if (balanceFactor < -1)//右子树高于左子树
{
if (diff(root->right) > 0)//RL的情况
root=RL_rotate(root);
else//RR的情况
root=RR_rotate(root);
}
return root;
}
//插入结点
Tree* Insert(Tree* root,ElenmentType k )
{
if (NULL == root)
{
root = new AVLNode(k);//如果根结点为null,则直接将值为根结点
if(root==NULL)
printf("创建失败");
return root;
}//递归返回条件
else if (k < root->value)
{
root->left = Insert(root->left, k);//递归左子树
//balance operation
root = Balance(root);//平衡操作包含了四种旋转
}
else if (k>root->value)
{
root->right = Insert(root->right, k);//递归右子树
//balance operation
root = Balance(root);//平衡操作包含了四种旋转
}
return root;
}
//中序遍历,获取的数列是有序的
void displayTree(Tree* node){
if(node == NULL) return;
if(node->left != NULL){
displayTree(node->left);
}
printf("%d ",node->value);
if(node->right != NULL){
displayTree(node->right);
}
}
//查找value,成功则返回该结点
Tree* binaryTreeSearch(Tree *node,int value){
if(node->value==value)
return node;
else if(node->value>value){
if(node->left!=NULL)
return binaryTreeSearch(node->left,value);
else return NULL;
}else{
if(node->right!=NULL)
return binaryTreeSearch(node->right,value);
else
return NULL;
}
}
void searchTree(Tree*node,int *i,int *a){
if(node == NULL) return ;
if(node->left != NULL){
searchTree(node->left,i,a);
}
a[*i++]= node->value;//中序遍历获取值列表 ,BST获取得到的是有序的,从小到大
if(node->right != NULL){
searchTree(node->right,i,a);
}
}
//寻找子树最大值
ElenmentType tree(Tree *node,int l=0){//l用于选择寻找最大值还是最小值。
int *a;
int i=0;
searchTree(node,&i,a);
printf("%d",i);
if(l==0)
return a[0];//最大值
else return a[i-1];//最小值
}
//删除结点
Tree* Delete(Tree *root, const ElenmentType k)
{
if (NULL == root)
return root;
if (!binaryTreeSearch(root,k))//查找删除元素是否存在
{
std::cerr << "Delete error , key not find" << std::endl;
return root;
}
if (k == root->value)//根节点
{
if (root->left!=NULL&&root->right!=NULL)//左右子树都非空
{
if (diff(root) > 0)//左子树更高,在左边删除
{
root->value = tree(root->left,0);//以左子树的最大值替换当前值
root->left = Delete(root->left, root->value);//删除左子树中已经替换上去的节点
}
else//右子树更高,在右边删除
{
root->value = tree(root->right,1);
root->right = Delete(root->right, root->value);
}
}
else//有一个孩子、叶子节点的情况合并
{
Tree * tmp = root;
root = (root->left) ? (root->left) :( root->right);
delete tmp;
tmp = NULL;
}
}
else if (k < root->value)//往左边删除
{
root->left = Delete(root->left, k);//左子树中递归删除
//判断平衡的条件与在插入时情况类似
if (diff(root) < -1)//不满足平衡条件,删除左边的后,右子树变高
{
if (diff(root->right) > 0)
{
root = RL_rotate(root);
}
else
{
root = RR_rotate(root);
}
}
}//end else if
else
{
root->right = Delete(root->right, k);
if (diff(root) > 1)//不满足平衡条件
{
if (diff(root->left) < 0)
{
root = LR_rotate(root);
}
else
{
root = LL_rotate(root);
}
}
}
return root;
}
int main(){
int a[10]={12,13,55,66,44,77,99,33,46,79};
Tree *root=NULL;
printf("第一次构建的平衡二叉树中序遍历:");
for(int i=0;i<10;i++){
root = Insert(root,a[i]);
}
displayTree(root);
printf("\n");
//查找33
int value = 33;
Tree* obj;
if((obj=binaryTreeSearch(root,value))==NULL){
printf("%d值不存在",value);
}
else printf("%d值存在,地址是%p",value,obj);
printf("\n");
root = Insert(root,5);
printf("插入了结点值为5的结点以后,中序遍历:") ;
displayTree(root);
printf("\n");
//删除33
Delete(root,value);
printf("删除结点33以后中序遍历:");
displayTree(root);
printf("\n");
//删除79
Delete(root,79);
printf("删除结点79以后中序遍历:");
displayTree(root);
return 0;
}
参考博客:
https://blog.csdn.net/zhangxiao93/article/details/51459743
https://zhuanlan.zhihu.com/p/56066942