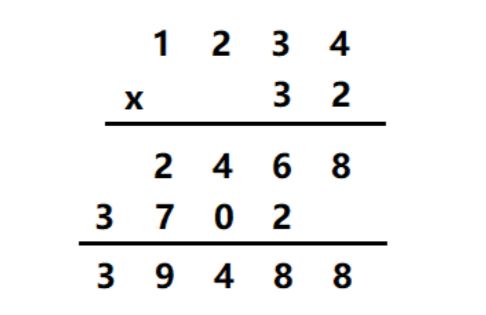基础算法--高精度(加减乘除)

高精度算法出现的原因

当参与运算的数的范围大大的超出了标准数据类型，如int（-2147483648 ~ 2147483647）或者long long的范围，就需要使用高精度算法来进行数的运算。高精度运算的特点是代码长度比较长，本质是对数学运算过程的模拟。既然不能使用标准数据类型，所以考虑使用字符串或者数组来存储这类大数据。

常用的一些最大值符号

• 0x7f7f7f7f —— 比int的最大值小一点
• 0x3f3f3f3f —— 比int的最大值的一半小一点
• INT_MAX —— int的最大值

#include 
#include 
using namespace std;

int main()
{
    cout << 0x7f7f7f7f << endl; //21 3906 2143
    cout << 0x3f3f3f3f << endl; //10 6110 9567
    cout << INT_MAX << endl;    //21 4748 3647
    return 0;
}

高精度算法一般有两种形式，①数组模拟 ②用STL中的vector容器 。
①：将字符串string中的每一位转化为int数组中的数；
②：用vector中的函数push_back(); pop_back(); back(); front(); begin(); 进行操作；

两者的模拟加法的大致思想是一样的，但STL容器可以在空间上随用随申请，而数组只能提前申请（a[100010]）固定空间。

高精度加法分析 模拟过程（核心代码）

1.加法（进位）

对于小数据，99 + 99 = 198，其运算过程如下：

这个是平时咱们计算的过程（红1表示进位）而写程序时咱们需要找到一个循环起来的方法，于是继续思考我们怎么用程序去实现进位以及进多少

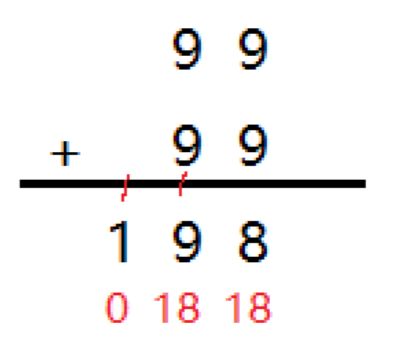
上图为直接对每一位相加之后的结果，从最低位（个位）看起，就可以发现结果的：个位8 = 18 % 10,十位9 = (18 + 1) % 10，百位1 = (0 + 1) % 10。这样就找到规律了：

先用进位表示每一位的和
每一位上的数字 = (上一位进位 + 加数上当前同位两数字的和）% 10
向下一位进位 = (上一位进位 + 同位两数字的和) / 10

注：这里是默认的a的长度>b的长度！ 程序中需要处理保证 a.size() > b.size()

（数组模拟，rr[]为结果）

for(int i=0; i<len; i++) 
{
    rr[i]+=aa[i]+bb[i];
    if(rr[i]>=10)  rr[i+1]++,rr[i]-=10;
}
if(rr[len])  len++;

（vector）

int t = 0;
vector<int> res;
for(int i=0; i<a.size()+1; i++)
{
    t += a[i];
    if(i < b.size())  t += b[i];
 
    res.push_back(t % 10);
    t /= 10; 
}

高精度加法运算步骤：

• 使用字符数组存储两个较大的数
• 把两个数逆序转化为整数数组
• 诸位相加运算，在运算的时候处理进位。
• 相加之后的结果最多比原来较长的数多一位，最后逆序输出即可

高精度加法模板

#include 
#include 

using namespace std;


// 高精度加法
// c = a + b
vector<int> add(vector<int> &A, vector<int> &B)
{
    vector<int> C;
    int t = 0; // 进位变量
    for(int i = 0; i < A.size() || i < B.size(); i ++)
    {
        if(i < A.size()) t += A[i];
        if(i < B.size()) t += B[i];
        C.push_back(t % 10);
        t /= 10;
    }
    if(t) C.push_back(1); 

    return C;
}

int main()
{
    string a, b; 
    vector<int> A, B;

    cin >> a >> b; // a = '123456'
    // 然后把每一位逆序抠出来放入vector中
    for (int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0'); // A = [6, 5, 4, 3, 2, 1]
    for (int i = b.size() - 1; i >= 0; i--) B.push_back(b[i] - '0');

    auto C = add(A, B);

    for(int i = C.size() - 1; i >= 0; i--) printf("%d", C[i]);
    return 0;
}

高精度减法分析 模拟过程（核心代码）

在高精度减法中，需要注意：

• 如果a < b，则需要先交换a与b，最后在输出结果前加上负号
• 在高精度计算时，如果a[i] < b[i]，则需要先向高位借一位

比较简单的情况是被减数的每一位都恰好比减数的每一位大，这里就不列举了；
比较复杂的就是下图这样有借位的情况：

1. 减法（借位）

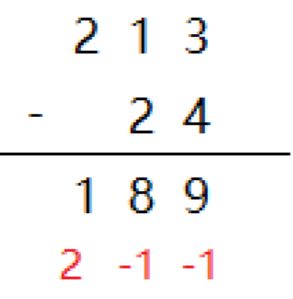
还是和加法一样先对每一位做减法（红字），然后从低位（个位）开始考虑借位变成下图（蓝字）

就可以找到规律：

每一位上的数字 = 同位减法，判断是否<0，小于则下一位(高位) 减1，本位(A+B) += 10
每位数字 =（同位减法 + 10 - 借位标记数）% 10，如果同位两数减法 <0 则标记1，否则标记0
（这个标记是在下一位(高位)时才开始起作用，模拟借位的过程，先判断有没有被借过位）

注：这里是默认的a的长度>b的长度！ 程序中需要处理保证 a.size() > b.size()

有了加法的启示这里如下计算

for(int i=0; i<lena; i++)
{
    rr[i]+=aa[i]-bb[i];
    if(rr[i]<0)  rr[i]+=10,rr[i+1]--;
}

（vector）

for(int i=0; i<a.size(); i++)
{
    t=a[i]-t;
    if(i<b.size())  t-=b[i];//和加法同理
 
    res.push_back((t+10)%10);
 
    if(t<0)  t=1;
    else  t=0;
}

2. 高精度减法模板

#include 
#include 

using namespace std;

//判断是否有 A >= B
bool cmp(vector<int> &A, vector<int> &B){
	if(A.size() != B.size()) return A.size() > B.size();
	for(int i = A.size() - 1; i >= 0; i --){
		if(A[i] != B[i])
			return A[i] > B[i];
	} 
	return true;
} 

// c = a - b
vector<int> sub(vector<int> &A, vector<int> &B)
{
    vector<int> C;
    for(int i = 0, t = 0; i < A.size(); i ++)
    {
    	t = A[i] - t;
    	if(i < B.size()) t -= B[i];
    	C.push_back((t + 10) % 10);
    	if(t < 0) t = 1;
    	else t = 0;
	}
	while(C.size() > 1 && C.back() == 0) C.pop_back(); // 抹去前导0 
	
	return C;
}

int main()
{
    string a, b; // 两个大整数数字过大，要用字符串读入
    vector<int> A, B;

    cin >> a >> b; // a = '123456'
    // 然后把每一位逆序抠出来放入vector中
    for (int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0'); // A = [6, 5, 4, 3, 2, 1]
    for (int i = b.size() - 1; i >= 0; i--) B.push_back(b[i] - '0');
	
	// 先判断A 和B的长度，如果B长就反过来
	if(cmp(A, B))
	{
		auto C = sub(A, B);
		for(int i = C.size() - 1; i >= 0; i--) printf("%d", C[i]);
	}else{
		auto C = sub(B, A);
		printf("-");
		for(int i = C.size() - 1; i >= 0; i--) printf("%d", C[i]);
	}
    
    return 0;
}

高精度乘法（高精度A * 低精度b）

在日常生活中，计算两个数字相乘，其过程是什么样子的呢？

// t每一位的进位
t = 0
C1 = (4 * 32 + t) % 10 == 8 // 个位
// 计算向下一位的进位
t = (4 * 32 + 0) / 10 == 12
C2 = (3 * 32 + 12) % 10 == 8 // 十位
t = (3 * 32 + 12) / 10 == 10
C3 = (2 * 32 + 10) % 10 == 4 // 百位
t = (2 * 32 + 10) / 10 == 7
C4 = (1 * 32 + 7) % 10 == 9 // 千位
t = (1 * 32 + 7) / 10 == 3 // 万位

得到 39488

容器法就相对简单一点，直接暴力每一位都乘一遍b，取模作为这一位上的结果，其实和加法类似。

每一位数字 = (a[i] * b + jw) % 10；
进位 += (a[i] * b + jw) / 10;

（vector）

vec mul(vec &a,int b)
{
    vec res;
    int t = 0;
 
    for(int i=0; i<a.size() || t; i++)
    {
        if(i < a.size())  t += a[i] * b;
        res.push_back(t % 10);
        t /= 10;
    }
}

最后需要注意的是，在高精度乘法中，得到的结果可能是多个0(如下图所示)，所以删除前导0需要用while循环而不是if语句。

高精度乘法模板

#include 
#include 

using namespace std;

// c = a * b
vector<int> mul(vector<int> &A, int &b)
{
    vector<int> C;
    
    int t = 0;
    // 循环条件，A没循环完或者t不为0 
    for(int i = 0; i < A.size() || t; i ++)
    {
    	// 如果A没循环完 
    	if(i < A.size()) t += A[i] * b;
    	C.push_back(t % 10);
    	t /= 10;
	}
	
	return C;
}

int main()
{
    string a;
    int b; 

    cin >> a >> b; 
    
    vector<int> A;
    for (int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');
	
	auto C = mul(A, b);
	for(int i = C.size() - 1; i >= 0; i--) printf("%d", C[i]);
    
    return 0;
}

高精度除法（高精度a÷低精度b）

首先1/31=0,

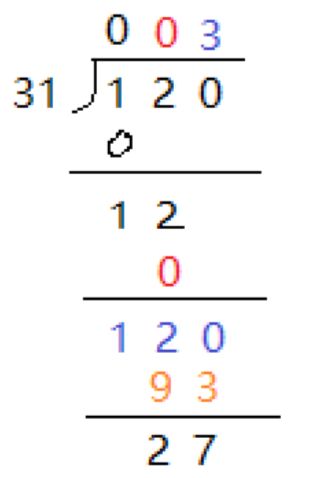
（1 * 10 + 2）/ 31 = 0，（（1*10+2）*10+0）/31=3 ，得到余数27，模拟完过程就可以找到规律了！

每位数字 =（上一位的余数 * 10+本位）/ 除数
余数 =（上一位的余数 * 10 + 本位）- 除数 * 结果位数字

由于除法的力量过于玄学，此处就只放vector版本了。

r=0;//余数要有初始值0
for(int i=a.size()-1; i>=0; i--)//从高位除起，所以后续不需要reverse
{
    r=r*10+a[i];
    res.push_back(r/b);
    r%=b;
}

高精度除法模板

思路

1.先把高精度数字存进A数组
2.调用除法函数
3.定义一个除法函数
（1）定义一个余数r，模拟实现除法，把r更新r = r * 10 + A[i];
（2）把r / b存进C数组
（3）r % 10继续更新r
（4）循环结束，计算出结果之后，去掉前导零
-第一步交换C数组的顺序
-第二步去掉前导零
-第三步换回来

#include 
#include 
#include 

using namespace std;

// c = a / b 商是C 余数是r 
vector<int> div(vector<int> &A, int b, int &r)
{
    vector<int> C;
    r = 0;
    for(int i = A.size() - 1; i >= 0; i --)
    {
    	r = r * 10 + A[i];
    	C.push_back(r / b);
    	r %= b;
	}
	reverse(C.begin(), C.end());
	while(C.size() > 1 && C.back() == 0) C.pop_back();
	
	return C;
}

int main()
{
    string a;
    int b; 

    cin >> a >> b; 
    
    vector<int> A;
    for (int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');
	
	int r;
	auto C = div(A, b, r);
	for(int i = C.size() - 1; i >= 0; i--) printf("%d", C[i]);
	
	cout << endl << r << endl;
    
    return 0;
}