算法宝典2——Java版本（此系列持续更新，这篇文章目前3道）（有题目的跳转链接）（此份宝典包含了二叉树的算法题）

注：由于字数的限制，我打算把算法宝典做成一个系列，一篇文章就20题！！！

目录

一、二叉树的算法题（目前3道）

1. 平衡二叉树（力扣）

2.  对称二叉树（力扣）

3. 二叉树的层序遍历（力扣）

---

一、二叉树的算法题（目前3道）

1. 平衡二叉树（力扣）

题目跳转链接https://leetcode.cn/problems/balanced-binary-tree/

题目：给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 ，空树也是平衡二叉树。

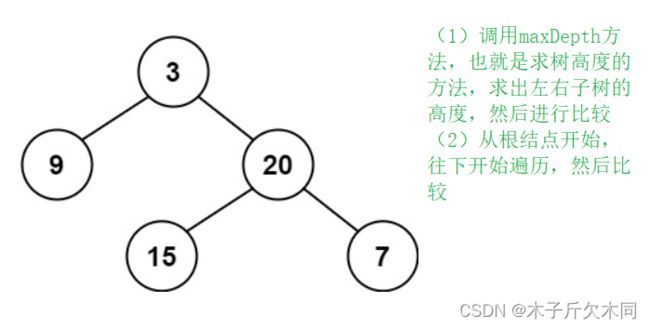
思路：

代码：

    // 获取二叉树的高度
    public int maxDepth(TreeNode root){
        if(root == null){
            return 0;
        }
        int leftCount = maxDepth(root.left);
        int rightCount = maxDepth(root.right);

        return (leftCount > rightCount) ? leftCount + 1 : rightCount + 1;
    }


    //判断是否为平衡二叉树
    public boolean isBalanced(TreeNode root) {
        //如果为空树，返回null
        if(root == null){
            return true;
        }
        //获取左右子树的高度
        int leftTreeHigh = maxDepth(root.left);
        int righTreeHigh = maxDepth(root.right);

        //isBalanced(root.left) && isBalanced(root.left)是判断左右子树是不是也满足平衡二叉树的定义
        return Math.abs(leftTreeHigh - righTreeHigh) < 2
                && isBalanced(root.left) && isBalanced(root.right);
    }

如果是按照上述代码的思路来写，此算法的时间复杂度就是O(n^2)！！！这是在是太大了！

什么原因造成的呢？

答：我们在求3结点的高度时，其实就把9结点的高度求出来了，但是递归到9结点的时候，又求了一次，导致重复求树的高度，有n个结点，每个结点就要求n次高度，也就是n*n！！！

所以我们可以把代码改一下：

    public int maxDepth2(TreeNode root) {
        //空树，证明没有子树，他的高度就是0
        if(root == null){
            return 0;
        }

        int leftH = maxDepth2(root.left);//只要左子树的高度返回是-1，表示左子树不满足平衡二叉树的定义
        if(leftH < 0)
            return -1;
        int rightH = maxDepth2(root.right);//只要右子树的高度返回是-1，表示左子树不满足平衡二叉树的定义
        if (rightH < 0)
            return -1;

        if(Math.abs(leftH - rightH) <= 1){
            return Math.max(leftH,rightH) + 1;//满足定义，返回高度最高的子树，并+1
        }else{
            return -1;//不满足定义，返回-1
        }

    }

    public boolean isBalanced2(TreeNode root) {
        return maxDepth2(root) >= 0;
    }

运行结果：

2.  对称二叉树（力扣）

题目跳转链接https://leetcode.cn/problems/symmetric-tree/

题目：给你一个二叉树的根节点 root ， 检查它是否轴对称。

思路：

和这道判断两个二叉树是不是一样的题目类似：算法宝典1——Java版本（此系列持续更新，这篇文章有20道）（有题目的跳转链接）（此份宝典包含了链表、栈、队列、二叉树的算法题）_木子斤欠木同的博客-CSDN博客

让左子树的左结点和右子树的右子树相比较，然后递归下去，然后就可以判断是不是对称二叉树！！！

代码：

    //判断对称树
    public boolean isSymmetricChild(TreeNode leftChild, TreeNode rightChild) {
        //这是路径的判断
        if (leftChild != null && rightChild == null || leftChild == null && rightChild != null) {
            return false;
        }
        if (leftChild == null && rightChild == null) {
            return true;
        }
        //这是值的判断
        if (leftChild.val != rightChild.val) {
            return false;
        }

        return isSymmetricChild(leftChild.left, rightChild.right)
                && isSymmetricChild(leftChild.right, rightChild.left);

    }

    public boolean isSymmetric(TreeNode root) {
        if (root == null) {
            return true;
        }
        return isSymmetricChild(root.left,root.right);
    }

运行结果：

3. 二叉树的层序遍历（力扣）

题目跳转链接https://leetcode.cn/problems/binary-tree-level-order-traversal/

题目：给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

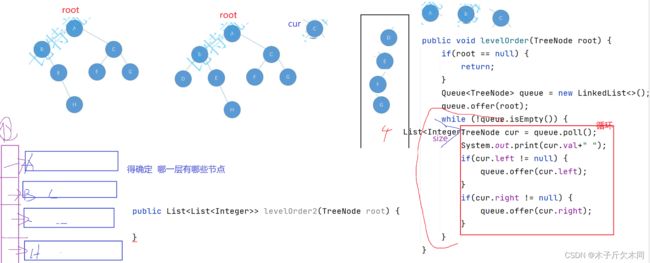
思路：

代码：

    //不带链表的形式
    public void levelOrder1(TreeNode root){
        if(root == null){
            return;
        }
        Queue queue = new LinkedList<>();
        queue.offer(root);
        while(!queue.isEmpty()){
            TreeNode poll = queue.poll();
            System.out.println(poll.val+ " ");
            if(poll.left != null){
                queue.offer(poll.left);
            }
            if(poll.left != null){
                queue.offer(poll.right);
            }
        }

    }

    
    //带链表的形式
    public List> levelOrder(TreeNode root) {
        List> List = new ArrayList<>();
        if(root == null){
             return List;
        }
        Queue queue = new LinkedList<>();
        queue.offer(root);
        while(!queue.isEmpty()){//第一层循环表示树什么时候遍历完
            int size = queue.size();
            List list = new ArrayList<>();
            while(size != 0){//第二层循环表示当前层次的元素数量
                TreeNode cur = queue.poll();
                size--;
                list.add(cur.val);//将元素保存到列表
                if(cur.left != null){
                    queue.offer(cur.left);
                }
                if(cur.right != null){
                    queue.offer(cur.right);
                }
            }
            List.add(list);
        }
        return List;
    }

运行结果：