图解LeetCode——1184. 公交站间的距离（难度：简单）
一、题目
环形公交路线上有 n 个站，按次序从 0 到 n - 1 进行编号。我们已知每一对相邻公交站之间的距离，distance[i] 表示编号为 i 的车站和编号为 (i + 1) % n 的车站之间的距离。
环线上的公交车都可以按顺时针和逆时针的方向行驶。
返回乘客从出发点 start 到目的地 destination 之间的最短距离。
二、示例
2.1> 示例1
【输入】distance = [1,2,3,4], start = 0, destination = 1
【输出】1
【解释】公交站 0 和 1 之间的距离是 1 或 9，最小值是 1。
2.2> 示例2
【输入】distance = [1,2,3,4], start = 0, destination = 2
【输出】3
【解释】公交站 0 和 2 之间的距离是 3 或 7，最小值是 3。
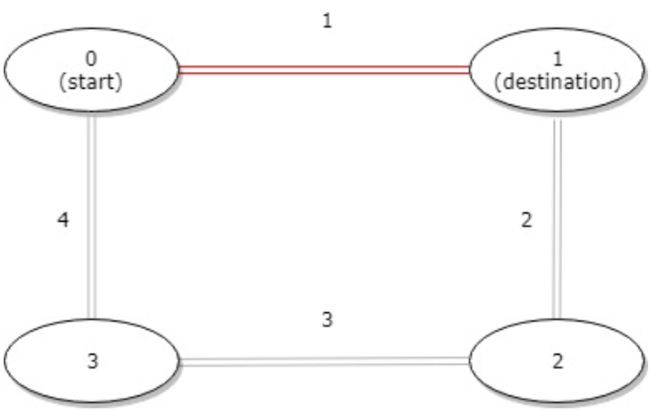
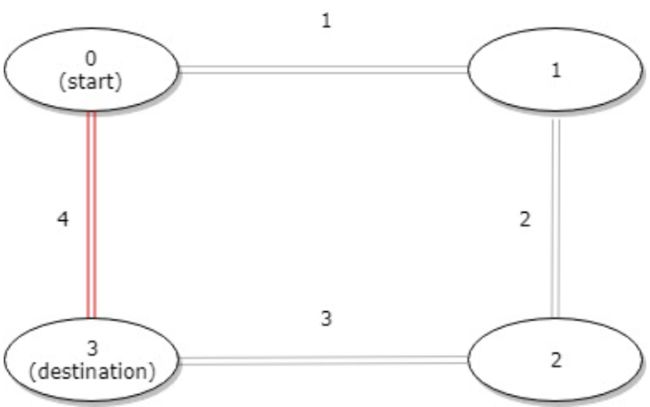
2.3> 示例3
【输入】distance = [1,2,3,4], start = 0, destination = 3
【输出】4
【解释】公交站 0 和 3 之间的距离是 6 或 4，最小值是 4。
提示：
- 1 <= n <= 10^4
- distance.length == n
- 0 <= start, destination < n
- 0 <= distance[i] <= 10^4
三、解题思路
3.1> 思路1：正逆向双指针
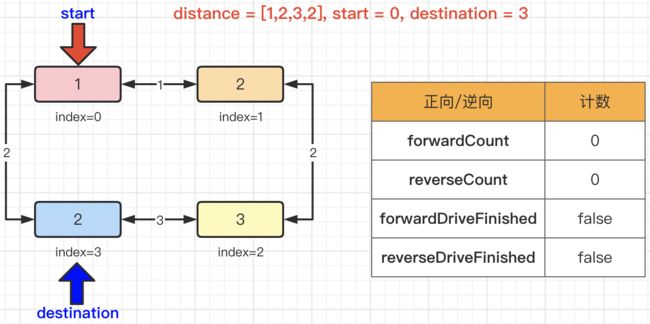
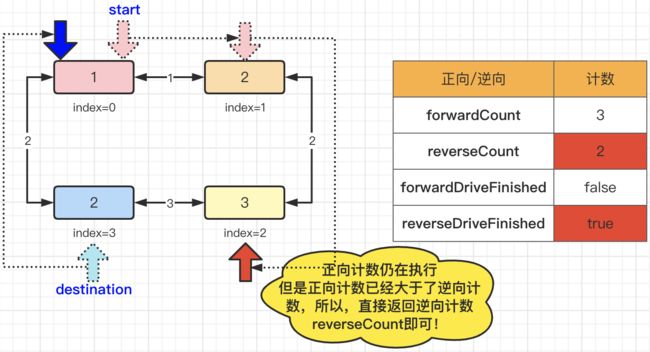
既然环线上的公交车都可以按顺时针和逆时针的方向行驶。那么我们分别通过两个指针，从起点开始和从终点开始，进行行驶，虽然从终点到起点的计算路线也是正向的，但是根据题意实际上都是从起点到终点，且经历的距离一样，所以，我们将从终点向起点计数称之为“逆向”。那么，起始情况下，正向计数：forwardCount=0，逆向计数：reverseCount=0，正向行驶是否结束：forwardDriveFinished=false，逆向行驶是否结束：reverseDriveFinished=false。如下图所示：
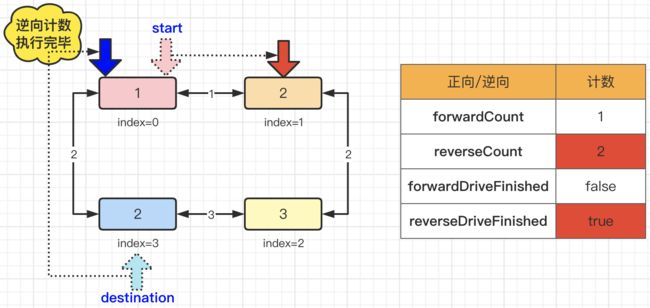
那么当第一次运行结束后，我们发现，逆向形式已经结束了（即：从index(3)到index(0)）,逆向计数：reverseCount=2。而正向形式还在进行中，其中正向计数：forwardCount=1。由于reverseCount > forwardCount，所以正向行驶继续。
那么由于逆向形式在上一轮循环中已经结束了，所以本轮只有正向行驶，行驶到index(2)的节点时，正向计数：forwardCount=3，由于reverseCount < forwardCount，所以，可以得出结论，逆向形式距离更短（虽然正向行驶还在继续进行中。。。），既然结果已经确定了，那么我们此时就可以结束正向行驶。返回reverseCount值作为结果。
3.2> 思路2：完整遍历后对比结果
思路一的好处是，对于正向或者逆向有一方步数较少时，我们可以不必等待步数较长一方执行完毕，只要以完成的一端可以确认路程最短，就可以结束遍历了。但是实现起来代码较多。而如果我们想要简便的代码实现的话，我们其实可以通过一次完整的循环遍历，再通过最终结果，来进行判断。
为什么可以通过一次完整遍历就能够确定呢？ 假设总的数组是[1, 2, 3, 4, 5, 6, 7, 8]，如果我们start=2，destination=7，那么在[2, 7)的范围内计数，就是正向行驶的距离。而由于整个路程是环路，即：是一个圆圈，所以范围之外的，就是逆向行驶的范围。而如果destination=2，start=7怎么办呢？其实和start=2，destination=7的计算方式是一样的，为了方便起见，我们只需要将destination=2，start=7变换为start=2，destination=7，就可以计数了。这种方式，实现代码会比较方便整洁。如下图所示：
四、代码实现
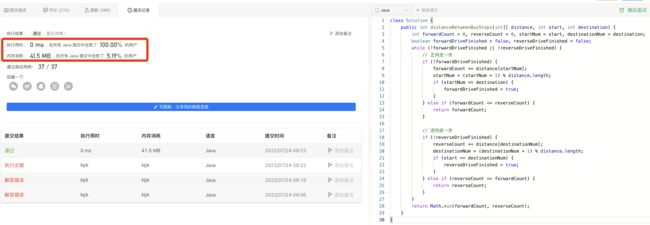
4.1> 实现1：正逆向双指针
public int distanceBetweenBusStops1(int[] distance, int start, int destination) {
int forwardCount = 0, reverseCount = 0, startNum = start, destinationNum = destination;
boolean forwardDriveFinished = false, reverseDriveFinished = false;
while (!forwardDriveFinished || !reverseDriveFinished) {
// 正向走一步
if (!forwardDriveFinished) {
forwardCount += distance[startNum];
startNum = (startNum + 1) % distance.length;
if (startNum == destination) {
forwardDriveFinished = true;
}
} else if (forwardCount <= reverseCount) {
return forwardCount;
}
// 逆向走一步
if (!reverseDriveFinished) {
reverseCount += distance[destinationNum];
destinationNum = (destinationNum + 1) % distance.length;
if (start == destinationNum) {
reverseDriveFinished = true;
}
} else if (reverseCount <= forwardCount) {
return reverseCount;
}
}
return Math.min(forwardCount, reverseCount);
}
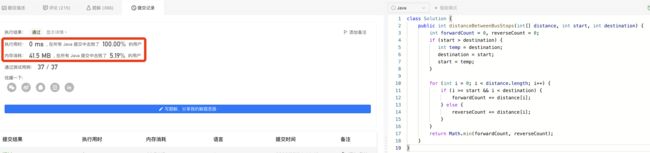
4.2> 实现2：完整遍历后对比结果
public int distanceBetweenBusStops2(int[] distance, int start, int destination) {
int forwardCount = 0, reverseCount = 0;
if (start > destination) {
int temp = destination;
destination = start;
start = temp;
}
for (int i = 0; i < distance.length; i++) {
if (i >= start && i < destination) {
forwardCount += distance[i];
} else {
reverseCount += distance[i];
}
}
return Math.min(forwardCount, reverseCount);
}
今天的文章内容就这些了：
写作不易，笔者几个小时甚至数天完成的一篇文章，只愿换来您几秒钟的点赞&分享。
更多技术干货，欢迎大家关注公众号@爪哇缪斯「干货分享，每天更新」
往期推荐
图解LeetCode——731. 我的日程安排表 II（难度：中等）
https://mp.csdn.net/mp_blog/creation/editor/125884328图解LeetCode——3. 无重复字符的最长子串（难度：中等）https://mp.csdn.net/mp_blog/creation/editor/125857066LeetCode精讲——21. 合并两个有序链表（难度：简单）https://mp.csdn.net/mp_blog/creation/editor/125840103LeetCode精讲——565. 数组嵌套（难度：中等）https://mp.csdn.net/mp_blog/creation/editor/125831251
题目来源：力扣（LeetCode）