LLM 07-大模型训练

LLM 07-大模型训练

上一章中，我们讨论了大语言模型（例如，Transformer）的模型结构。
在本章中，我们将讨论如何训练大语言模型。
本章分成目标函数和优化算法两部分。

7.1 目标函数

我们研究三类语言模型的目标函数：

1. 只包含解码器（Decoder-only）的模型（例如，GPT-3）：计算单向上下文嵌入（contextual embeddings），一次生成一个token
2. 只包含编码器（Encoder-only）的模型（例如，BERT）：计算双向上下文嵌入
3. 编码器解码器（Encoder-decoder）模型（例如，T5）：编码输入，解码输出

我们可以使用任何模型将token序列映射到上下文嵌入中（例如，LSTM、Transformers）：

$$\varphi :V^L\to {\mathbb{R}}^{d\times L}.$$
$$\left[\text{the},\text{mouse},\text{ate},\text{the},\text{cheese}\right]\stackrel{\varphi }{\Rightarrow }\left[\left(\genfrac{}{}{0ex}{}{1}{0.1}\right),\left(\genfrac{}{}{0ex}{}{0}{1}\right),\left(\genfrac{}{}{0ex}{}{1}{1}\right),\left(\genfrac{}{}{0ex}{}{1}{-0.1}\right),\left(\genfrac{}{}{0ex}{}{0}{-1}\right)\right].$$

7.1.1 Decoder-only 模型

回想一下，自回归语言模型定义了一个条件分布：
$$p(x_i\mid x_{1:i-1}).$$
我们将其定义如下：

• 将$x_{1:i-1}$映射到上下文嵌入$\varphi (x_{1:i-1})$。
• 应用嵌入矩阵$E\in {\mathbb{R}}^{V\times d}$来获得每个token的得分$E\varphi (x_{1:i-1}{)}_{i-1}$。
• 对其进行指数化和归一化，得到预测$x_i$的分布。

简洁地：
$$p(x_{i+1}\mid x_{1:i})=softmax(E\varphi (x_{1:i}{)}_i).$$

7.1.1.1 最大似然

设$\theta$是大语言模型的所有参数。设$D$是由一组序列组成的训练数据。
然后，我们可以遵循最大似然原理，定义以下负对数似然目标函数：
$$O(\theta )=\sum _{x\in D}-\log p_{\theta }(x)=\sum _{x\in D}\sum _{i=1}^L-\log p_{\theta }(x_i\mid x_{1:i-1}).$$

并且，有很多的方法可以有效地优化这一目标函数。

7.1.2 Encoder-only 模型

7.1.2.1 单向到双向

使用上述最大似然可以训练得到Decoder-only模型，它会产生（单向）上下文嵌入。但如果我们不需要生成，我们可以提供更强的双向上下文嵌入。

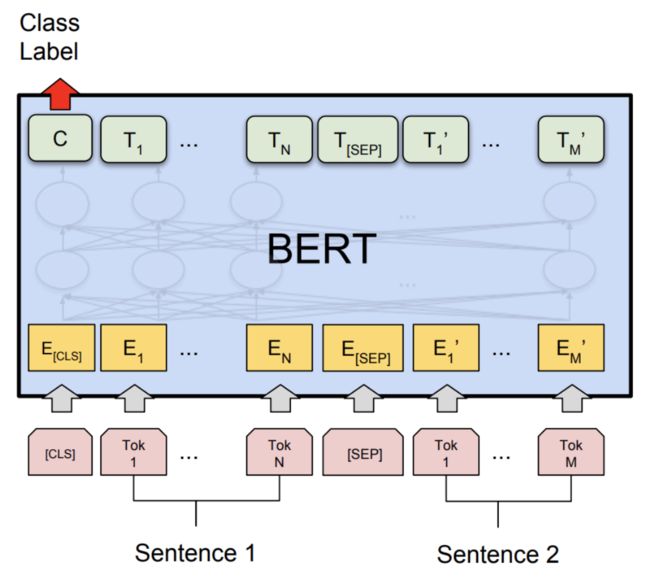
7.1.2.2 BERT

我们首先介绍BERT的目标函数，它包含以下两个部分：

• 掩码语言模型（Masked language modeling）
• 下一句预测（Next sentence prediction）

以自然语言推理（预测隐含、矛盾或中性）任务中的序列为例：

$$x_{1:L}=[\text{[CLS]},\text{all},\text{animals},\text{breathe},\text{[SEP]},\text{cats},\text{breathe}].$$

其中有两个特殊的token：

• $\text{[CLS]}$：包含用于驱动分类任务的嵌入
• $\text{[SEP]}$：用于告诉模型第一个序列（例如，前提）与第二个序列（例如，假设）的位置。

根据上一章的公式，BERT模型定义为：
$$\text{BERT}(x_{1:L})={\text{TransformerBlock}}^{24}(\text{EmbedTokenWithPosition}(x_{1:L})+\text{SentenceEmbedding}(x_{1:L}))\in {\mathbb{R}}^{d\times L},$$

其中，$\text{SentenceEmbedding}(x_{1:L})$根据序列返回以下两个矢量之一

• 对于$\text{[SEP]}$左边的，返回$e_A\in {\mathbb{R}}^d$
• 对于$\text{[SEP]}$右边的，返回$e_B\in {\mathbb{R}}^d$

BERT-large有$n_{\text{heads}}=16$个注意头，并且$d_{\text{model}}=1024$，总共355M个参数。

7.1.2.2.1 掩码语言模型

掩码语言模型的基本思想是通过加噪然后预测来进行训练：

$$[\text{the},\text{[MASK]},\text{ate},\text{[MASK]},\text{cheese}]\Rightarrow [\text{the},\text{mouse},\text{ate},\text{the},\text{cheese}].$$

更普遍地说，我们可以将其视为类似于去噪自动编码器，其中我们映射有噪声/不完整版本${\tilde{x}}_{1:L}$，并尝试重建原始$x_{1:L}$。

$${\tilde{x}}_{1:L}\Rightarrow x_{1:L}.$$

建模：我们首先定义模型分布。给定输入${\tilde{x}}_{1:L}$及其上下文嵌入，模型独立地预测每个token：
$$p(x_i\mid {\tilde{x}}_{1:L})=\text{softmax}(E\varphi ({\tilde{x}}_{1:L}{)}_i).$$

**掩码：**我们定义了一个（随机）噪声函数$A({\tilde{x}}_{1:L}\mid x_{1:L})$：
$$\underset{\text{original}}{x_{1:L}}\stackrel{A}{\Rightarrow }\underset{\text{noised}}{{\tilde{x}}_{1:L}}.$$

以下是$A$的定义：

• 假设$I\subset \{1,\dots ,L\}$代表所有位置中随机的15%。
• 对于每个$i\in I$：
  • 以0.8的概率，${\tilde{x}}_i\leftarrow \text{[MASK]}$
  • 以0.1的概率，${\tilde{x}}_i\leftarrow x_i$
  • 以0.1的概率，${\tilde{x}}_i\leftarrow \text{random word from }\mathcal{V}$

减少分布偏移： 如果我们总是使用$\text{[MASK]}$来替换$I$中选定的token，则：

• 在训练期间，输入到BERT的都是带$\text{[MASK]}$的序列。
• 而在测试时，我们会输入没有$\text{[MASK]}$的句子，这将导致分布发生变化。一种启发式的解决方法是在20%的时间内用真实单词替换。

7.1.2.2.2 下一句预测

回想一下，BERT是在拼接好的成对句子上训练的。下一句预测的目标是预测第二句是否跟随第一句。
$$[\text{[CLS]},\text{the},\text{mouse},\text{ate},\text{the},\text{cheese},\text{[SEP]},\text{it},\text{was},\text{full}]\Rightarrow 1.$$
$$[\text{[CLS]},\text{the},\text{mouse},\text{ate},\text{the},\text{cheese},\text{[SEP]},\text{hello},\text{world}]\Rightarrow 0.$$

然后使用$\text{[CLS]}$的嵌入来做二分类。

7.1.2.2.3 数据集

$\mathcal{D}$是按如下方式构造的一组样本$(x_{1:L},c)$：

• 令$A$是语料库中的一个句子。
• 以0.5的概率，$B$是下一句话。
• 以0.5的概率，$B$是语料库中的一个随机句子。
• 令$x_{1:L}=[\text{[CLS]},A,\text{[SEP]},B]$
• 令$c$表示$B$是否是下一句。

7.1.2.2.4 训练目标

BERT的训练目标是：
$$\mathcal{O}(\theta )=\sum _{(x_{1:L},c)\in \mathcal{D}}\underset{\text{masked language modeling}}{{\mathbb{E}}_{I,{\tilde{x}}_{1:L}\sim A(\cdot \mid x_{1:L},I)}[\sum _{i\in I}-\log p_{\theta }({\tilde{x}}_i\mid x_{1:L})]}+\underset{\text{next sentence prediction}}{-\log p(c\mid \varphi (x_{1:L}{)}_1)}.$$

稍后我们将讨论训练，这里简要总结一下BERT：

• BERT（以及ELMo和ULMFiT）表明，一个统一的体系结构（Transformer）可以用于多个分类任务。
• BERT真正将NLP社区转变为预培训+微调的范式。
• BERT显示了深度双向上下文嵌入的重要性，尽管通过模型大小和微调策略可能会弥补这一点（p-tuning）。

7.1.2.3 RoBERTa

RoBERTa对BERT进行了以下改进：

• 删除了下一句预测这一目标函数（发现它没有帮助）。
• 使用更多数据训练（16GB文本 $\Rightarrow$ 160GB文本）。
• 训练时间更长。
• RoBERTa在各种基准上显著提高了BERT的准确性（例如，在SQuAD上由81.8到89.4）。

7.1.3 Encoder-decoder 模型

任务示例（表格生成文本）：
$$[\text{name},\text{:},\text{Clowns},\text{|},\text{eatType},\text{:},\text{coffee},\text{shop}]\mathbb{R}ightarrow[\text{Clowns},\text{is},\text{a},\text{coffee},\text{shop}].$$

回想一下编码器-解码器模型（例如，BART、T5）：

• 首先像BERT一样对输入进行双向编码。
• 然后像GPT-2一样对输出进行自回归解码。

7.1.3.1 BART (Bidirectional Auto-Regressive Transformers)

BART (Lewis et al. 2019)是基于Transformer的编码器-解码器模型。

• 使用与RoBERTa相同的编码器架构（12层，隐藏维度1024）。
• 使用与RoBERTa相同的数据进行训练（160GB文本）。

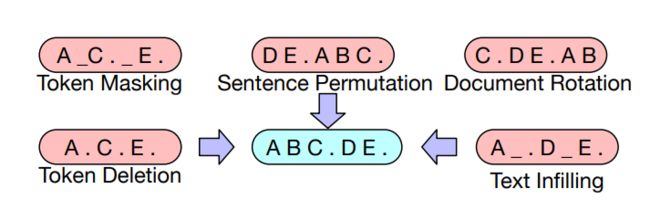
BART使用了以下变换$A({\tilde{x}}_{1:L}\mid x_{1:L})$：

基于BERT的实验，最终模型进行以下了变换：

• 掩码文档中30%的token
• 将所有子句打乱

最后，通过微调，BART在分类和生成任务上都展示了强大的效果。

7.1.3.2 T5 (Text-to-Text Transfer Transformer)

T5 (Raffel et al., 2020)是另一种基于Transformer的编码器-解码器模型。

预训练任务：
给定一段文本，在随机位置将其分割为输入和输出：
$$[\text{the},\text{mouse}]\Rightarrow [\text{ate},\text{the},\text{cheese}].$$

论文尝试了许多不同的无监督目标：

并发现“i.i.d. noise, replace spans”效果最好（尽管许多目标相似）。

论文还将所有经典的NLP任务放在一个统一的框架中，称为“Text-to-Text”任务：

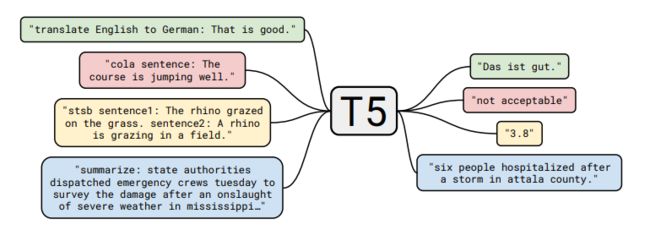
以分类任务任务为例，不同模型的差异如下：

• BERT使用$\text{[CLS]}$的嵌入来预测。
• T5、GPT-2、GPT-3等（生成模型）将分类任务转换成自然语言生成。

注意：

• 论文对整个pipline的许多方面（数据集、模型大小、训练目标等）进行了深入研究。
• 基于这些见解，他们训练了一个11B的模型。

7.2 优化算法

现在，我们将注意力转向如何优化目标函数。

为了简单起见，让我们以自回归语言模型为例：
$$O(\theta )=\sum _{x\in D}-\log p_{\theta }(x).$$

7.2.1 随机梯度下降（SGD）

最简单的优化算法是用小批量进行随机梯度下降，该算法的步骤如下：

• 初始化参数${\theta }_0$
• 重复以下步骤：
  • 采样小批量$B_t\subset D$
  • 根据梯度更新参数：
    $${\theta }_t\leftarrow {\theta }_{t-1}-\eta \frac{1}{|B_t|}\sum _{x\in B_t}{\nabla }_{\theta }(-\log p_{\theta }(x)).$$

优化的关键点包括：

1. 我们希望参数$\theta$可以快速收敛
2. 我们希望优化在数值上是稳定的
3. 我们希望内存高效（尤其是对于大模型）

这些点往往相互矛盾（例如，通过低精度训练，可以实现快速收敛、减少内存占用，但是会导致训练不稳定）

因此，我们可以从几个层次来进行优化：

1. 针对经典优化：二阶方法、约束优化等。
2. 针对机器学习：随机方法、隐式正则化+早停法
3. 针对深度学习：初始化、归一化（更改模型架构）
4. 针对大语言模型：由于稳定性问题，学习率和一些直觉（例如，二阶方法）仍然有用，但要使大语言模型有效训练，还需要克服许多其他独特的挑战。不幸的是，其中大部分内容都是特别的，人们对此了解甚少。

7.2.2 Adam (adaptive moment estimation)

Adam算法拥有以下两个创新：

1. 引入动量（继续朝同一方向移动）。
2. 参数${\theta }_0$的每个维度都有一个自适应（不同）的步长（受二阶方法启发）。

它的步骤如下：

• 初始化参数${\theta }_0$
• 初始化动量$m_0,v_0\leftarrow 0$
• 重复以下步骤：
  • 采样小批量$B_t\subset D$
  • 按照如下步骤更新参数：

    • 计算梯度
      $$g_t\leftarrow \frac{1}{|B_t|}\sum _{x\in B_t}{\nabla }_{\theta }(-\log p_{\theta }(x)).$$

    • 更新一阶、二阶动量
      $$\begin{gathered} m_t\leftarrow {\beta }_1{m}_{t-1}+(1-{\beta }_1)g_t \\ {v}_t\leftarrow {\beta }_2{v}_{t-1}+(1-{\beta }_2)g_t^2 \end{gathered}$$

    • 对偏差进行修正
      $$\begin{gathered} {\hat{m}}_t\leftarrow m_t/(1-{\beta }_1^t) \\ {\hat{v}}_t\leftarrow v_t/(1-{\beta }_2^t) \end{gathered}$$

    • 更新参数
      $${\theta }_t\leftarrow {\theta }_{t-1}-\eta {\hat{m}}_t/(\sqrt{{\hat{v}}_t}+ϵ).$$

存储占用分析：

Adam将存储从2倍的模型参数（${\theta }_t,g_t$）增加到了4倍（${\theta }_t,g_t,m_t,v_t$）。

7.2.3 AdaFactor

AdaFactor是一种为减少存储占用的优化算法。它有如下特点：

• 它不储存$m_t,v_t$这样的$O(m\times n)$矩阵，而是存储行和列的和$O(m+n)$并重构矩阵
• 去除动量
• 它被用来训练T5
• AdaFactor可能使训练变得困难（见Twitter thread和blog post）

7.2.4 混合精度训练

混合精度训练是另一种减少存储的方法

• 通常来说，默认的精度是：FP32（32位浮点）
• 其他可选精度：FP16（16位浮点），但问题是任何小于$2^{-24}$的值都会变为0。
• 解决方案：将主权重存储在FP32中，并在FP16中执行其他所有操作。
• 损失缩放：按比例放大损失，以避免梯度数值太小。
• 结果：存储减少了一半。

7.2.5 学习率

• 通常情况下，学习率会随着时间的推移而衰减。
• 对于Transformer模型，我们实际上需要通过预热（warmup）提高学习率。
• Huang et al., 2020表明，一个潜在的原因是防止层归一化的梯度消失，导致使用Adam优化器训练时不稳定。

7.2.6 初始化

• 给定矩阵$W\in {\mathbb{R}}^{m\times n}$，标准初始化（即，xavier初始化）为$W_{ij}\sim N(0,1/n)$。
• GPT-2和GPT-3通过额外的$1/\sqrt{N}$缩放权重，其中$N$是残差层的数量。
• T5将注意力矩阵增加一个$1/\sqrt{d}（$代码）。

以GPT-3为例，使用的参数如下：

• Adam参数：${\beta }_1=0.9,{\beta }_2=0.95,ϵ=10^{-8}$
• 批量小：320万个token（约1500个序列）
• 使用梯度剪裁（$g_t\leftarrow g_t/\min (1,\Vert g{\Vert }_2)$）
• 线性学习率预热（前3.75亿个token）
• 余弦学习率衰减到10%
• 逐渐增加批大小
• 权重衰减设为0.1