python求三位数的最大公约数和最小公倍数(3种算法)
一、穷举法求最大公约数
可以利用循环穷举的方法,看是否能整除这三个数。若能整除这三个数,则输出其中的最小的数即为最小公倍数。
代码如下:
def Sort_xyz(x,y,z,):
l = [x,y,z]
l.sort()
return l
def Gcd(x,y,z):
x,y,z = Sort_xyz(x,y,z)
for i in range(1,z + 1):
if x % i == 0 and y % i == 0 and z % i == 0:
gcd = i
return gcd二、辗转相除法
又名欧几里德算法,用较小数除较大数,再用出现的余数(第一余数)去除除数,再用出现的余数(第二余数)去除第一余数,如此反复,直到最后余数是0为止。如果是求两个数的最大公约数,那么最后的除数就是这两个数的最大公约数。 求三个数时先算出两个数的最大公约数,然后用这个数与第三个数求最大公约数,所得数字即为最大公约数
代码如下
#将三个数由小到大排列
def Sort_xyz(x,y,z,):
l = [x,y,z]
l.sort()
return l
def Gcd(x,y,z):
x,y,z = Sort_xyz(x,y,z)
while y != 0:
temp = y
y = x % y
x = temp
if x < z:
temp = x
x = z
z = temp
while z != 0:
temp = z
z = x % z
x = temp
return x三、辗转相减法
即尼考曼彻斯法。例如 :两个自然数35和14,用大数减去小数,35-14=21,21-14=7,此时,7小于14,要做一次交换,把14作为被减数,即14-7=7,再做一次相减,结果为0,这样也就求出了最大公约数7。
代码如下:
#将三个数由小到大排列
def Sort_xyz(x,y,z,):
l = [x,y,z]
l.sort()
return l
def Gcd3(x,y,z):
x,y,z = Sort_xyz(x,y,z)
while x != y :
if x > y:
x = x - y
else:
y = y - x
if y < z:
temp = y
y = z
z = temp
while y != z :
if y > z:
y = y - z
else:
z = z - y
return z四、穷举法求最小公倍数
先求出三个数中最大的一个数max,用max乘以1,2,3,4........
当max*n%num1==0 and max*n%num2==0 and max*n%num3==0
这时max*n即最小公倍数
代码如下:
#将三个数由小到大排列
def Sort_xyz(x,y,z,):
l = [x,y,z]
l.sort()
return l
def Lcm1(x,y,z):
x,y,z = Sort_xyz(x,y,z)
i = 1
j = 0
while True:
j = x * i
if j%x==0 and j%y==0 and j%z==0:
break
i += 1
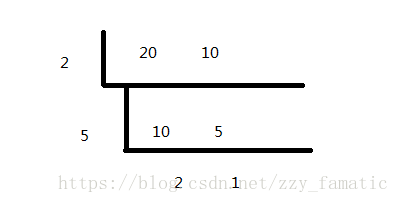
return j五、短除法求最小公倍数
最小公倍数=为2*5*2=20
计算三个数时先求出两个数的最小公倍数,在和另一个数求最小公倍数
代码如下:
#将三个数排列
def Sort_xyz(x,y,z,):
l = [x,y,z]
l.sort()
return l
def Lcm2(x,y,z):
lcm = 1
k = max(x,y,z)
for i in range(2,x+1):
#对循环是否结束进行标记
flag = True
while flag:
flag = False
if x % i == 0:
x = x / i
flag = True
if y % i == 0:
y = y / i
flag = True
if z % i == 0:
z = z / i
flag = True
if flag:
lcm *= i
k = max(x,y,z)
return lcm
六、公式法
由于两个数的乘积等于这两个数的最大公约数与最小公倍数的积。即(a,b)×[a,b]=a×b。所以,求两个数的最小公倍数,就可以先求出它们的最大公约数,然后用上述公式求出它们的最小公倍数。
代码如下:
def Lcm3(x,y,z):
gcd = Gcd(x,y)
lcm = (x*y)/gcd
gcd = Gcd(lcm,z)
lcm = (lcm*z)/gcd
return lcm