微分几何笔记(2) —— 曲线的参数化

第二周讲完了Klingenberg的第一章Curves，做一点微小的笔记。
分成三个部分，本篇讲曲线的弧长参数；下一篇讲一般的Frenet标架及方程组；再下一篇讲二维三维空间曲线的curvature。

GTM51对入门者会难一些，因为直接从最一般的$n$维情况入手，再回头看二三维空间中的曲线，相比之下 Calculus and Analysis in Euclidean Space 这本UTM的Chapter 8 Parametrized Curves 算是相当新手友好的入门内容，由二三维曲线推广到一般情况。

借用宋老师的话，微分几何的本质是几何，主要通过微积分的手段，用数和函数来刻画几何图形的性质。可能在学习的时候会觉得明明很直观，几何画出来就是这样的，但是要用规范的严格语言说出来很困难。所以说也是一个打基础的课程，先学会怎样严格的表述，在这基础之上才能正确的使用微积分这个工具。
 
 

2.1 参数曲线(Parametrized Curves)

Definition 2.1.1  参数曲线 是指一个光滑映射(smooth mapping)：$$c:I\to {\mathbb{R}}^n$$ 这里$n\ge 1$, $I\subseteq {\mathbb{R}}^n$ 且非空。
更进一步，如果 $\forall t\in I,c^{\prime }(t)\ne 0$，称这样的曲线是正则的(regular).
 

也就是说我们平时说的“曲线”，其实是一个映射，平时说“点在曲线上”，是指这一点，如$c(t)$在这个映射的像集中。

我们一般都要求曲线是正则的，因为是光滑映射，所以导数不等于零$\iff$导数的范数不等于零，直观理解是这样的曲线是不会停下的，也因此我们可以用隐函数定理，反函数定理等。

如果$I$是不是开区间，定义的意思是，存在一个包含$I$的开区间$I^{\ast }$，使得$c^{\ast }$在$I^{\ast }$上是一个光滑映射，并且$c^{\ast }|I=c$，这样就解决了端点无定义的问题。

这里我们说的参数曲线都是“光滑”的，这个要求也太高了，不过现在考虑的都是很显然，一眼能够看明白的曲线，以后会逐步放宽。
 
 

Definition 2.1.2
i)切空间(Tangent Space):
对$x_0\in {\mathbb{R}}^n$，切空间是指所有以$x_0$为起点的$n$维向量所构成的空间，记作$T_{x_0}{\mathbb{R}}^n$.

ii)沿着曲线$c$的向量场(Vector field along $c:I\to {\mathbb{R}}^n$):
指一个可微映射$X:I\to {\mathbb{R}}^n$，$\forall t\in I$，$X(t)\in T_{c(t)}{\mathbb{R}}^n$.

iii)切向量场(Tangent vector field of $c:I\to {\mathbb{R}}^n$):
指一个沿着$c$的向量场，其中在$c(t)$处的向量由切向量$t\mapsto c^{\prime }(t)$给出。
 
 
这里主要是规定向量的起点位于什么地方。
切空间是相当于把$x_0$当成原点所建立的${\mathbb{R}}^n$空间，所有$x_0\in {\mathbb{R}}^n$中向量起于$x_0$.
沿着曲线的向量场是指在曲线的每一点上都"生长"着一些向量，比如下图中所示那样：

 

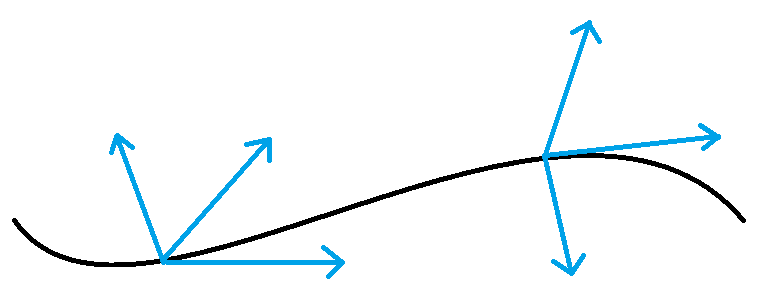
图1：生长在曲线上的向量场

接下来一节讲讲弧长参数曲线(parametrization by arc length)，用曲线的弧长做参数，这样做可以简化计算过程。
 
 

2.2 弧长参数曲线(Parametrization by Arc Length)

Definition 2.2.1 如果一个映射$\varphi :I\to I^{\prime }$是光滑的，而且其逆映射${\varphi }^{-1}:I^{\prime }\to I$也是光滑的，称映射$\varphi$是微分同胚(Diffeomorphism)

Definition 2.2.2(Equivalence of Curves) 两条曲线 $c:I\to {\mathbb{R}}^n$ 和 $\tilde{c}:\tilde{I}\to {\mathbb{R}}^n$ 之间如果存在一个微分同胚 $\varphi$，使得 $\tilde{c}=c\circ \varphi$，则称$\varphi$是一个参数变换(parameter transformation).并且如果 ${\varphi }^{\prime }>0$，称这样的参数变换是保持定向的(orientation preserving) .

由参数变换所得的曲线构成一个所有 ${\mathbb{R}}^n$中曲线的等价类（满足自反性(reflexive)，对称性(symmetric)和传递性(transitive)），给这个等价类起个名字叫做 非参数化曲线(unparametrized curve).

其实我们可以把$I$看成是关于时间的集合，把$c(t)$看成一个空间中随时间运动的轨迹，这样$c^{\prime }(t)$就是速度，而$|c^{\prime }(t)|$则是速率。通过不同的参数变换，改变了质点沿曲线运动一定长度所需要的时间（区间$I$的长度），从而改变了质点运动的速率。我们特别关注的，是其中以单位速度运动的参数曲线，也就是$|c^{\prime }(s)|=1$ 的曲线。

Definition 2.2.3 (Arc length of a curve) 光滑曲线$c:I\to {\mathbb{R}}^n$上两点$t_0,t\in I,t_0<t$之间的弧长为：
$$L(t_0,t)={\int }_{t_0}^t|c^{\prime }(\tau )|d\tau$$.

事实上，这个积分对于$C^1$及更好的曲线都是well-define的，但是对连续的曲线不一定对，因为存在在闭区间上长度无穷的连续曲线。

比如 $y=sin\frac{1}{x}$ 在 $x=0$ 附近非道路连通；

比如把$[0,1]$映射到$[0,1]\times [0,1$的皮亚诺曲线；

再比如可以构造出$[0,1]\to [0,1]\times [0,1]$的双射：https://www.zhihu.com/question/301263376

把有限弧长的连续曲线，称为可求长曲线(rectifiable curve)

Definition 2.2.4 (Parametrization by arc length) 曲线$c(s)$称为弧长参数化的，如果$L(s_0,s)=s-s_0$，等价的说，$|c^{\prime }(s)|=1,\forall s\in I$.

试想，现在我们通过改变曲线的参数，使得之前需要通过复杂的含绝对值积分才能得到的弧长，现在只需要做差就能够得到。通过这种方式，让计算变得如此简单，如果对后面计算曲率的过程有了解，就能感觉到这是一件非常令人振奋的事情，而且要是能把任意曲线都弧长参数化，那这事已经好的不能再好了。

直觉上来说这事肯定是对的，因为弧长参数化的直观理解就是以单位速度沿着曲线运动，这只要曲线本身的光滑程度够就行。

那既然是以单位速度沿着曲线运动，我只要以弧长为参数不就好了吗？这样用原来给定参数曲线的弧长来做参数，经过一个单位时间，等于经过一个单位弧长，等于沿弧长以单位速度运动。太妙了。

接下来是本篇笔记铺垫到现在，为了阐述的主要命题：

Proposition 2.2.5 每一个正则曲线(Regular Curve)都等价于一个弧长参数化曲线。

Proof .
存在性：假设$c:I\to {\mathbb{R}}^n,t\mapsto c(t)$为一光滑曲线，我们想找一个$\tilde{c}:\tilde{I}\to {\mathbb{R}}^n,s\mapsto \tilde{c}(s)$，满足$c(t)$和$\tilde{c}(s)$的像集是一模一样的。
为此我们需要找一个映射$\ell :I\to \tilde{I}$. 之前我们考虑过，以$c$的弧长，来作为$\tilde{c}$的参数，也就是$s=\ell (t)={\int }_{t_0}^t|c^{\prime }(\tau )|d\tau$，写成交换图的形式：

因为${\ell }^{\prime }(t)=|c^{\prime }(t)|>0$ (c is regular), 由反函数定理知道反函数存在且可导。这样，我们把交换图上边以$t$为参数的映射，转化成了下边以$s$为参数的映射，接下来只需要验证$|{\tilde{c}}^{\prime }(s)|=1$，由隐函数求导法则以及变上限函数的导数：
$c^{\prime }(t)={\tilde{c}}^{\prime }(\ell (t))={\tilde{c}}^{\prime }(s){\ell }^{\prime }(t)={\tilde{c}}^{\prime }(s)|c^{\prime }(t)|$
两边同时取绝对值，就得到了结论，存在性得证，并且知道$\tilde{c}(s)=c\circ {\ell }^{-1}(s)$.
唯一性是显然的，假设有两条参数曲线都满足条件导数为1，因为是正则曲线，所以其导数可以去掉绝对值，同时积分。这样可以看出，参数起始于同一点的弧长参数化曲线是唯一的，证毕。
 
 

2.3 一般参数曲线化成弧长参数曲线的例子

怎么把一般参数曲线化成弧长参数曲线，其实在上面命题的证明中已经构造出来了。

数学证明很多时候是构造性的，怎么证明，就怎么使用；而有的证明只是用严格话的语言论述，说明条件满足某些定义，这种证明算是在教我们该怎么“说话”。二者都是需要的，但是对于推动数学进展来说，更重要的是前者，因为启发性更强，毕竟，好的证明使我们更加聪明。

这里求${\ell }^{-1}$可能会是很困难的一步，因为$\ell$本来是个积分函数，且变量在积分上限，这就意味着很多时候，我们只能在形式上表示出来，并不能真正求出${\ell }^{-1}$（which mathematicians always say.）
举两个能求出来弧长参数化曲线的例子：

Example 2.3.1 $c:\mathbb{R}\to {\mathbb{R}}^2$, given by $c(t)=(\cos e^t,\sin e^t)$.

这个形式一看就跟圆脱不了关系，只是问题在于他不是以单位速度沿圆周运动的，那么将他弧长参数化之后，应该会变成标准圆的参数方程才对。

Solution:
先确定自变量的范围，这里$t\in (-\infty ,\infty )$,

$s=\ell (t)={\int }_{-\infty }^t|c^{\prime }(\tau )|d\tau ={\int }_{-\infty }^t{e}^{\tau }d\tau =e^t,s\in (0,\infty )$

所以$t={\ell }^{-1}(s)=\ln s,s\in (0,\infty )$.

最终的弧长参数化曲线为：
$\tilde{c}(s)=c\circ {\ell }^{-1}(s)=(\cos s,\sin s).$

这也印证了我们的想法。
 

Example 2.3.2 $c:[\frac{\pi }{2},\frac{3\pi }{2}]\to {\mathbb{R}}^2$, given by $c(t)=(t-\sin t,1-\cos t)$.

这里的曲线称为摆线(cycloid)，且$\theta$取的是其中间的一段：

Solution:
$s=\ell (t)={\int }_{\frac{\pi }{2}}^t|c^{\prime }(\tau )|d\tau ={\int }_{\frac{\pi }{2}}^t\sqrt{(1-\cos \tau {)}^2-{\sin }^2\tau }d\tau ={\int }_{\frac{\pi }{2}}^{t}2\sin \frac{\tau }{2}d\tau$
$\Rightarrow s=-4\cos \frac{t}{2}+2\sqrt{2},s\in [0,4\sqrt{2}],$

因为在$\frac{t}{2}\in [\frac{\pi }{4},\frac{3\pi }{4}]$上$\cos$函数导数恒不为0，反函数存在，所以最终：

$\tilde{c}(s)=c\circ {\ell }^{-1}(s)=(t-\sin t,1-\cos t)$

$\Rightarrow \tilde{c}(s)=(2\arccos \frac{2\sqrt{2}-s}{4}-\frac{2\sqrt{2}-s}{8}\sqrt{(2\sqrt{2}+s{)}^2-2s^2},2-2(\frac{2\sqrt{2}-s}{4}{)}^2).$

我要知道结果会是这样，一开始我就不愿意求了。所以接下来的问题是有没有对一般非弧长参数适用的公式呢，这个问题将会在第四次笔记中讲到。

 

至此，曲线的参数化就讲完了，下一篇就初入微分几何的正题——Frenet标架。

 

参考：
[1]W. Klingenberg.   A course in differential geometry.   Translated from the German by David Hoffman. Graduate Texts in Mathematics, Vol. 51. Springer-Verlag, 1978.
[2]J. Shurman.   Calculus and Analysis in Euclidean Space   Undergraduate Texts in Mathematics,Springer-Verlag, 2016.
[3]厦门大学杨波老师的主页：http://math-faculty.xmu.edu.cn/display.aspx?tid=149