区块链中如何验证交易存在？ 如何验证交易不存在？Merkel Proof和Merkel Tree的应用——中山大学软件工程学院专选课《区块链》课堂小测

Merkle Proof 是一种用于验证区块链中某一特定交易确实存在于某一区块内的机制。这一机制是基于 Merkle Tree（默克尔树）的结构来进行的。

证明存在

默克尔树是一种二叉树，其中每个叶节点是某个交易的哈希值，每个非叶节点是其子节点哈希值合并后再哈希的结果。

验证步骤：

1. 找到交易哈希：首先，你需要知道你想要验证的交易的哈希值。

2. 获取路径（Merkle Path）：从该交易的哈希开始，找到一条路径通向默克尔树的根。这个路径上会有一系列的哈希值，这些哈希值是用于从叶节点（你的交易）计算到根节点的。

3. 重新计算并比对根哈希：使用这些路径上的哈希值和给定的交易哈希，通过相同的哈希函数重新计算出一个根哈希。

4. 验证根哈希：如果重新计算出的根哈希与区块头中存储的默克尔根相匹配，那么这个交易就被认为是存在于该区块内的。

示例：

假设你要验证交易 T3 存在于以下的默克尔树中：

                          Root=H(H1+H2)
                         /              \
                  H1=H(T1+T2)        H2=H(T3+T4)
                 /          \        /          \
               T1          T2     T3          T4

你只需要以下几个哈希值来验证 T3：

• T3 的哈希（自己有）
• T4 的哈希（路径上的兄弟节点）
• H1 的哈希（路径上的“叔叔”节点）

然后，用这些哈希值重构一个新的默克尔根，并与原来的默克尔根进行比对。如果一致，就证明了 T3 确实存在于该区块中。

这种方式的优点是，你不需要知道区块内所有的交易，只需要路径上的几个哈希值就能完成验证，大大提高了效率。

证明不存在？

如果先对下面的交易用哈希值进行排序。

验证步骤：

1. 寻找相邻节点：找出该交易哈希应该插入的位置，以及应该与其相邻的两个存在于树中的交易（一个比它小，一个比它大）。

2. 提供路径证明：提供从这两个相邻交易到默克尔根的路径（Merkle Path）。

3. 验证与相邻交易的顺序关系：验证这两个交易确实是按照预期的顺序排序的（一个比目标交易小，一个比目标交易大）。

4. 重新计算默克尔根：使用提供的Merkle Path和相邻交易的哈希值来重新计算默克尔根。

5. 比对默克尔根：如果重新计算出的默克尔根与区块头中的默克尔根匹配，那么就证明了该交易确实不存在于这个区块中。

这样，你就提供了一个加密学证明，表明某个特定的交易并不在排序的默克尔树中。

示例：

假设我们有一个简化的默克尔树，其中包含四个交易：T1, T2, T3 和 T4。它们的哈希值分别是 H(T1), H(T2), H(T3) 和 H(T4)。这些交易已经按照哈希值排序。默克尔树和其对应的默克尔根（Merkle Root）将如下：

                 Merkle Root = H( H(T1 + T2) + H(T3 + T4) )
                        /                             \
                H(T1 + T2)                    H(T3 + T4)
               /          \                  /           \
           H(T1)        H(T2)           H(T3)         H(T4)

现在，我们要证明一个交易 T5（假设其哈希值为 H(T5)）不存在于这个树中。

步骤

1. 寻找相邻节点: 假设 H(T5) 的值介于 H(T2) 和 H(T3) 之间，那么这两个哈希值就是它的相邻节点。

2. 提供路径证明: 为了证明 T5 不存在，我们需要提供从 H(T2) 和 H(T3) 到 Merkle Root 的路径。这个路径包括 H(T1 + T2) 和 H(T3 + T4)。

3. 验证与相邻交易的顺序关系: 确保 H(T2) < H(T5) < H(T3)。

4. 重新计算默克尔根: 使用提供的路径和相邻交易的哈希值重新计算 Merkle Root。这个重新计算的值应该与原来的 Merkle Root 相匹配。

5. 比对默克尔根: 如果重新计算出的 Merkle Root 与区块头中的 Merkle Root 匹配，那么证明了 T5 确实不存在于这个默克尔树中。

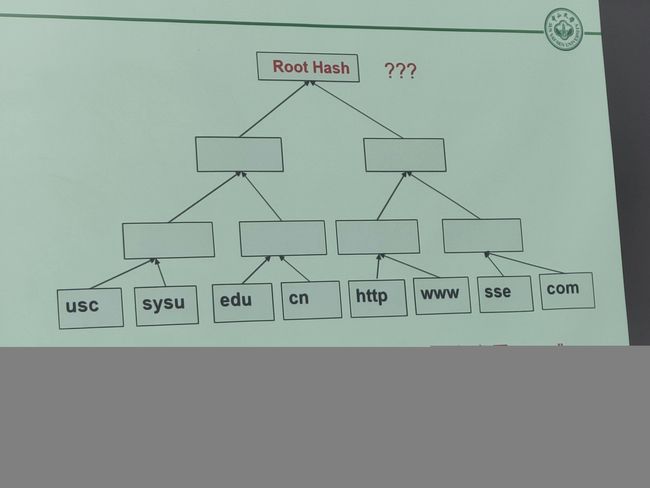
课堂小测

H(usc):df77c5138ae76098923e7fd44343e18781f7f1ecb6c36dd5d98bc8a522dcd2e0

H(sysu):2a5511e342dfa8c10702aab2c4c7ff9c1ffebb42c37aa04a412dfaed54fca809

H(edu):e613bb442bf089c035920266fa19f94a0972c896f212eda804d265c3b3f0e3f9

H(cn):ff2082aa78aea80a27cb4fb91f0350153702c16dce790a77f0bb0bfbf6899977

H(http):e0603c499aae47eb89343ad0ef3178e044c62e70ae2309b35591d1d49a3211ec

H(www):7c2ecd07f155648431e0f94b89247d713c5786e1e73e953f2fe7eca39534cd6d

H(sse):fe3811fe21af748f53a05a169da84013d11253a53e3ef80355d20419fd89042e

H(com):71b4f3a3748cd6843c01e293e701fce769f52381821e21daf2ff4fe9ea57a6f3

从左到右设为1~8。

H(12):f5b0b7461833a4e2ac56657c150f11bb63ed0e36ec43af5a96eaf7d3242c3807

H(34):80e017a08b6183caa32503a5bad1ac90e74dfff1b320aaca21f473d0e3967317

H(56):eea8657e41e85285f413dd2d16cf08b37740e60ca5cbd6b91ee3f12b064699d8

H(78):c368e3368d22f4097c5fe9217b45515b5dc1ccf8f673e3abb90d965a23b71ded

H(1234):a11727da1551ad53dfb52845e41ffbc3da34ae860e7fcd78ff01de9a8e618eef

H(5678):ccb6f11b960f33d2716403bf052653539ec868e8db3120f4a449782b6d3ef324

H(12345678):1f60e41b8d3f13a560ac45aabcf837d2dfc08e7fa20fb8953f348d0cd2a6ada3

最后对比程序发现对不上，经过检查，发现是H(78)搞错了

H(78)：e843dfb9cad6473137ca1fc850ad73ae6c248363463af387e33212d610a458d8

H(5678)：251a199817adefc2e538ace4cc1840c00183a1cd3d676efdf52e58b1498ba436

H(12345678)：b879b81f6b08259a3616e6a0ce690d33bba80c25d1768fe54ae570259f065c77

要证明存在交易"sysu"就要找到一条"merkel path",sysu对应H(2)，那path（最后能算出H(12345678）在这里是H(1),H(34),H(5678)。

H(12)=H(H(1) H(2))

        =f5b0b7461833a4e2ac56657c150f11bb63ed0e36ec43af5a96eaf7d3242c3807

之前算过H(34)=80e017a08b6183caa32503a5bad1ac90e74dfff1b320aaca21f473d0e3967317

那么H(1234)=a11727da1551ad53dfb52845e41ffbc3da34ae860e7fcd78ff01de9a8e618eef

H(12345678)=b879b81f6b08259a3616e6a0ce690d33bba80c25d1768fe54ae570259f065c77

与之前算出来的Root Hash相同，故存在。

代码实现

import hashlib


# 计算SHA256哈希
def sha256(text):
    return hashlib.sha256(text.encode()).hexdigest()


# 创建默克尔树
def merkle_tree(leaf_nodes):
    if len(leaf_nodes) == 1:
        return leaf_nodes[0]

    parent_nodes = []

    for i in range(0, len(leaf_nodes), 2):
        left = leaf_nodes[i]
        if i + 1 < len(leaf_nodes):
            right = leaf_nodes[i + 1]
        else:
            right = left  # 奇数个节点时复制最后一个

        parent = sha256(left + right)
        print(f"左子节点：{left}, 右子节点：{right}, 父节点：{parent}")  # 打印出每一步生成的哈希值
        parent_nodes.append(parent)

    return merkle_tree(parent_nodes)


# 生成并验证默克尔证明
def merkle_proof(target, leaf_nodes, merkle_root):
    for leaf in leaf_nodes:
        if sha256(target) == leaf:
            calculated_root = merkle_tree(leaf_nodes)
            if calculated_root == merkle_root:
                return "存在"
    return "不存在"

'''
usc
sysu
edu
cn
http
www
sse
com
'''
# 主程序
n = int(input("请输入节点数量："))
leaf_nodes = []

print("请输入{}个字符串：".format(n))
for _ in range(n):
    text = input()
    leaf_nodes.append(sha256(text))

merkle_root = merkle_tree(leaf_nodes)
print("Merkle Root:", merkle_root)

target = input("请输入要验证的字符串：")
result = merkle_proof(target, leaf_nodes, merkle_root)
print("字符串{}在给定的字符串列表中{}".format(target, result))