算法(二)——数组章节和链表章节
数组章节
(1)二分查找
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
class Solution {
public int search(int[] nums, int target) {
//二分查找法
int right=nums.length-1;
int left=0;
while(left<=right){
int mid=(right+left)/2;
if(target<nums[mid]){
right=mid-1;
}else if(target>nums[mid]){
left=mid+1;
}else{
return mid;
}
}
return -1;
}
}
(2)双指针——移除元素
- 给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
- 不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
- 元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
class Solution {
public int removeElement(int[] nums, int val) {
//双指针(quick-遍历数组 slow-将不等于val的元素依次插入新数组)
int slow=0;
for(int quick=0;quick<nums.length;quick++){
if(nums[quick]!=val){
nums[slow]=nums[quick];
slow++;
}
}
return slow; //slow指针指向空位,等待插入,所以slow值等于新数组长度
}
}
(3)有序数组的平方
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
class Solution {
public int[] sortedSquares(int[] nums) {
// 结果数组
int n = nums.length;
int[] result = new int[n];
// 双指针
int left = 0;
int right = n - 1;
while (left <= right) {
if (Math.pow(nums[left], 2) >= Math.pow(nums[right], 2)) {
result[n - 1] = (int) Math.pow(nums[left], 2);
left++;
} else {
result[n - 1] = (int) Math.pow(nums[right], 2);
right--;
}
n--;
}
return result;
}
}
(4)长度最小的子数组
- 给定一个含有 n 个正整数的数组和一个正整数 target 。
- 找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
class Solution {
public int minSubArrayLen(int target, int[] nums) {
int res = 2147483647;//整数最大值
int len;
int sum=0;
int i=0;//i 为窗口开始位置,j 为窗口终止位置
for(int j=i;j<nums.length;j++){
sum+=nums[j];
while(sum>=target){
len=j-i+1;
res=Math.min(len,res);
sum-=nums[i++];//不断移动i,直到区间内的和< target
}
//跳出while循环后,遍历继续j,j指针重新与i指针合并
}
return res==2147483647? 0:res;//数组总和都达不到target,res没有改变
}
}
(5)螺旋矩阵
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
class Solution {
public List<Integer> spiralOrder(int[][] matrix) {
//这个二维数组行列不确定
List<Integer> result = new ArrayList<>();
//matrix.length 行数
//matrix[0].length 列数
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
return result;
}
int rows = matrix.length; //行
int cols = matrix[0].length; //列
//定义四个变量top、bottom、left、right,分别表示当前遍历的上边界、下边界、左边界和右边界。
//初始时,上边界为0,下边界为行数减1,左边界为0,右边界为列数减1。
int top = 0, bottom = rows - 1, left = 0, right = cols - 1;
while (top <= bottom && left <= right) {
// 从左到右
if(right!=0){ //判断只有一列的情况
for (int i = left; i <= right; i++) {
result.add(matrix[top][i]);
}
top++;
}
// 从上到下
if(bottom!=0){//判断只有一行的情况
for (int i = top; i <= bottom; i++) {
result.add(matrix[i][right]);
}
right--;
}
// 从右到左
if (top <= bottom) {
for (int i = right; i >= left; i--) {
result.add(matrix[bottom][i]);
}
bottom--;
}
// 从下到上
if (left <= right) {
for (int i = bottom; i >= top; i--) {
result.add(matrix[i][left]);
}
left++;
}
}
return result;
}
}
链表章节
(6)移除链表中的元素
给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val == val 的节点,并返回 新的头节点 。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
//该方法没有头结点
public ListNode removeElements(ListNode head, int val) {
// 处理头节点为需要删除的节点的情况
while (head != null && head.val == val) {//这个while需要注意
head = head.next;
}
// 处理链表为空的情况(你前面持续删除首结点,当然得判断链表是不是被你删空嘞)
if (head == null) {
return head;
}
// 遍历链表,删除节点
ListNode cur = head;
while (cur.next != null) {
if (cur.next.val == val) {
cur.next = cur.next.next;
} else {
cur = cur.next;
}
}
return head;
}
}
(7)设计链表
定义一个双链表,并实现它的基本操作
//双链表
class ListNode{
int val;
ListNode next;
ListNode prev;
ListNode(){}
ListNode(int val){
this.val=val;
}
}
class MyLinkedList {
//链表长度
int size;
//虚拟头结点
ListNode head;
public MyLinkedList() {
size = 0;
head = new ListNode(0);
head.next = null;
head.prev = null;
}
//根据索引查询并返回元素
public int get(int index) {
if (index < 0 || index >= size) {
return -1;
}
ListNode curr = head;
for (int i = 0; i <= index; i++) {
curr = curr.next;
}
return curr.val;
}
//头插法
public void addAtHead(int val) {
ListNode newNode = new ListNode(val);
newNode.next = head.next;
newNode.prev = head;
if (head.next != null) {
head.next.prev = newNode;
}
head.next = newNode;
size++;
}
//尾插法
public void addAtTail(int val) {
ListNode newNode = new ListNode(val);
ListNode curr = head;
while (curr.next != null) {
curr = curr.next;
}
curr.next = newNode;
newNode.prev = curr;
size++;
}
//按索引添加新结点
public void addAtIndex(int index, int val) {
if (index < 0 || index > size) {
return;
}
if (index == 0) {
addAtHead(val);
return;
}
if (index == size) {
addAtTail(val);
return;
}
ListNode newNode = new ListNode(val);
ListNode curr = head;
for (int i = 0; i < index; i++) {
curr = curr.next;
}
newNode.next = curr.next;
newNode.prev = curr;
curr.next.prev = newNode;
curr.next = newNode;
size++;
}
//按索引删除结点
public void deleteAtIndex(int index) {
if (index < 0 || index >= size) {
return;
}
ListNode curr = head;
for (int i = 0; i < index; i++) {
curr = curr.next;
}
curr.next = curr.next.next;
if (curr.next != null) {
curr.next.prev = curr;
}
size--;
}
}
/**
* Your MyLinkedList object will be instantiated and called as such:
* MyLinkedList obj = new MyLinkedList();
* int param_1 = obj.get(index);
* obj.addAtHead(val);
* obj.addAtTail(val);
* obj.addAtIndex(index,val);
* obj.deleteAtIndex(index);
*/
(8)翻转链表
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode reverseList(ListNode head) {
//双链表
ListNode cur=head;
ListNode pre=null;
ListNode temp=new ListNode();
while(cur!=null){
temp=cur.next;
cur.next=pre;
//这两步不能颠倒
pre=cur;
cur=temp;
}
return pre;
}
}
(9)两两交换链表中的结点
给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode swapPairs(ListNode head) {
ListNode demo=new ListNode();//虚拟头结点
demo.next=head;//让虚拟头结点指向head首结点
ListNode cur=demo;//遍历指针
ListNode first;//保存需要交换的第一个结点
ListNode second;//保存需要交换的第二个结点
ListNode temp;//临时变量存储结点
//开始遍历
while(cur.next!=null && cur.next.next!=null){//分别考虑链表长度为偶数和奇数情况
first=cur.next;
second=cur.next.next;
//开始交换位置
temp=cur.next.next.next;//保存第二组结点的第一个结点
//开始交换
cur.next=second;
second.next=first;
first.next=temp;
//cur需要变到下一组的前面结点
cur=first;//注意此时链表的顺序以及改变
}
return demo.next;
}
}
(10)删除链表的倒数第n个结点
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
//虚拟头结点
ListNode demo=new ListNode(-1);
demo.next=head;
//双指针法
ListNode slow=demo;
ListNode fast=demo;
//fast首先走n + 1步
//因为只有这样同时移动的时候slow才能指向删除节点的上一个节点(方便做删除操作
for (int i = 0; i < n ; i++){
fast=fast.next;
}
//双指针开始同步右移
while(fast.next!=null){
fast=fast.next;
slow=slow.next;
}
//此时slow指针指向倒数第N+1个结点
//开始删除
slow.next=slow.next.next;
//这里返回的是demo.next而不是head;
return demo.next;
}
}
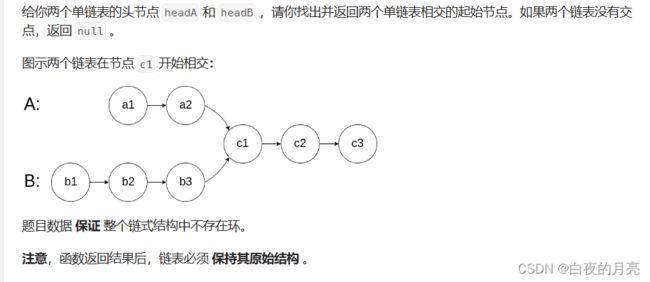
(11)链表相交
"双指针法"具体步骤如下:
- 创建两个指针p1和p2,分别指向两个链表的头节点。
- 同时移动两个指针p1和p2,每次移动一个节点。
- 当其中一个指针到达链表末尾时(即指向null),将它指向另一个链表的头结点。
- 继续移动两个指针,直到它们相遇或者都指向null。
- 如果两个指针相遇,则说明两个链表有交点,返回该节点。
- 如果两个指针都指向null,则说明两个链表没有交点,返回null。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
if(headA==null || headB==null) return null;
//双指针法
ListNode p1=headA;
ListNode p2=headB;
//开始遍历
while(p1!=p2){
if(p1==null){
p1=headB;
}else{
p1=p1.next;
}
if(p2==null){
p2=headA;
}else{
p2=p2.next;
}
}
return p1;
}
}
(12)环型链表
- 给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
- 如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。
- 为了表示给定链表中的环,评测系统内部使用整数 pos来表示链表尾连接到链表中的位置(索引从 0开始)。
- 如果 pos 是 -1,则在该链表中没有环。
- 注意:pos不作为参数进行传递,仅仅是为了标识链表的实际情况。
- 不允许修改 链表。
/**
* Definition for singly-linked list.
* class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode detectCycle(ListNode head) {
//数学题(追击问题)
//有环必相遇
//第一步:判断是否有环
ListNode slow=head;
ListNode fast=head;
while(fast!=null && fast.next!=null){
slow=slow.next;//一次移动一个结点
fast=fast.next.next;//一次移动两个结点
if(slow==fast){//有环
//第一步:找环的第一个结点
//根据公式,存在n=1,即快指针在第二圈途中与慢指针相遇,浪漫吗? 累成狗了,浪漫个屁。
ListNode slowRecord=slow;//记录彼此的第一次邂逅,慢指针依旧原地开始走
ListNode fastEx=head;//快指针回head首结点重新开始追
while(slowRecord!=fastEx){
//这回两人都得一步一步走,直到相遇,相遇点即为环入口
slowRecord=slowRecord.next;
fastEx=fastEx.next;
}
return slowRecord;
}
}
//无环无缘喽
return null;
}
}