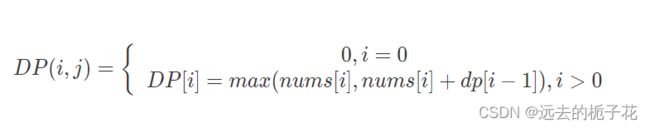数据结构与算法 -- 动态规划子数组问题
一、子数组问题
如果一道题目给定的输入是一个数组,那么满足以下条件的问题就是动归子数组问题:
1、问题符合动归典型特征
2、题目的答案是题设数组的子数组,或者来源于子数组。
二、回文子串个数
1、问题描述
给定一个字符串,你的任务是计算这个字符串中有多少个回文子串。具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
示例1:
输入:"dp"
输出:2
解释:共有两个回文子串,分别为 "d", "p"。
示例2:
输入:"aaa"
输出:6
解释:共有六个回文子串,分别为 "a", "a", "a", "aa", "aa", "aaa"。注意题设,具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串,因此像 "aa" 和 "aa" 就是两个不同的回文子串。2、算法分析
1)初始状态
从问题的示例就可以看出(当然也很容易想到),单个字符一定是它自己的回文。
2)状态参数
由于我们需要在整个字符串(数组)中确定子串(子数组)的位置,因此需要两个变量来约束和确定子串,一个是子串的起始位置,另一个是结束位置。在算法的执行过程中,起始和结束位置是变化的,因此它们是状态参数。
3)状态决策
一个范围较小的回文子数组 ➕ 额外元素后,再看它是不是回文子数组。更大范围的问题是由前面的子问题 ➕ 当前决策推导出来的,当前的决策就是如果向子问题的两边分别扩充一个元素,那么当前问题是否还是回文。
4)备忘录
使用二维数组作为动归解法的备忘录。设 DP[i][j],其中 i 是子数组的起始位置,j 是结束位置,而 DP[i][j] 代表以i为起点以j为终点的字符串是否是回文字符串。
3、状态方程
4、算法实现
package main
import "fmt"
func DP(str string) int {
strSlice := []byte(str)
ans := 0
// 创建备忘录
m := len(str)
n := len(str)
dp := make([][]bool, m)
for i := range dp{
dp[i] = make([]bool, n)
}
// 初始化状态
for i := 0; i < len(str); i++ {
dp[i][i] = true
ans++
}
for j := 1; j < m; j++ { // 遍历每一个结束位置
for i := 0; i < j; i++ { // 遍历每一个开始位置
dp[i][j] = strSlice[i]==strSlice[j] && (j-i <3 || dp[i+1][j-1]); //状态转移方程
if dp[i][j] {
ans++
}
}
}
return ans;
}
func main() {
str := "aaa"
fmt.Println(DP(str)) // 输出答案
}三、最大子数组之和
1、问题描述
问题:给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
输入:[-2, 1, -3, 4, -1, 3, -5, 1, 2]
输出:6
解释:连续子数组 [4,-1, 3] 的和最大为 6。2、算法分析
1)初始状态
初始状态即备忘录中以i为终点的子数组和为定义的最小值;
2)状态参数
状态参数就清晰明了,即 n ;
3)状态决策
要决策的就是是否要将当前子问题中额外的数字放入整个计算当中,以获得“更大”的子数组之和。
4)备忘录
DP[i][j] 对应的值是起始位置为 i 结束位置为 j 构成的最大子的子数组和。那么原问题的答案应该存放在 DP[0][n] 当中。但是这样设计备忘录,问题就复杂了。由于我们要求的只是一个最值,所有子问题最终要规约到从索引 0 到 n,因此没有必要同时记录子数组的起始和结束位置。 将 DP[i][j] 简化成 DP[i]。
3、状态方程
4、算法实现
package main
import "fmt"
func DP(array []int, length int) int {
// 创建备忘录
dp := make([]int, length)
// 初始化状态
for i := 1; i < length; i++ {
dp[i] = -10000
}
dp[0] = array[0]
// 转移方程转换实现
for j := 1; j < length; j++ {
if array[j] > dp[j-1]+array[j] {
dp[j] = array[j]
} else {
dp[j] = dp[j-1]+array[j]
}
}
//获取结果
max := -10000
for i := 0; i < length; i++ {
if max < dp[i] {
max = dp[i]
}
}
return max
}
func main() {
array := []int{-2, 1, -3, 4, -1, 3, -5, 1, 2}
length := len(array)
fmt.Println(DP(array, length)) // 输出答案
}