数据结构——二叉树提升
二叉树题型练习
- 前言
- 一、节点个数以及高度等
- 二、二叉树OJ题
-
- 二叉树的前序遍历
- 二叉树的中序遍历
- 二叉树的后序遍历
- 单值二叉树
- 二叉树最大深度
- 检查两颗树是否相同
- .翻转二叉树
- 对称二叉树
- 另一颗树的子树
- 总结
前言
现在我们开始一轮新的自我提升吧！
二叉树的题目当然也更有难度！
没有什么是生来就会的，尤其是代码这一方面
更是讲究熟能生巧，现在的我们学习代码编程就像婴儿学习灵活使用双手一般
相信以后的我们也可以像使用双手一般毫无困难地编写程序！
一、节点个数以及高度等
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
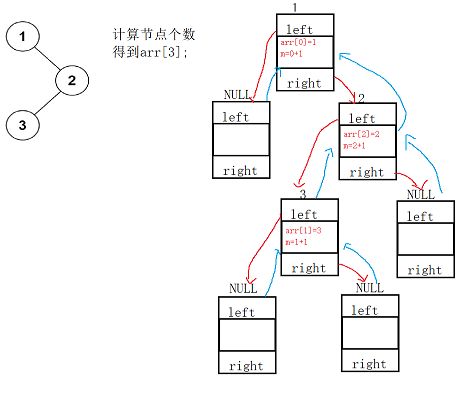
size保存的是代码执行到当前位置符合条件的节点个数
1.节点个数代码实现
int TreeSize(BTNode* root) {
static int size = 0;
if (root == NULL)
return 0;
else
++size;
TreeSize(root->left);
TreeSize(root->right);
return size;
}
思路解析：
2.叶子节点个数代码实现
int TreeLeafSize(BTNode* root) {
if (root == NULL)
return 0;
if (root->left == NULL && root->right) {
return 1;
}
return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}
思路解析：
3.第k层节点个数代码实现
int TreeKLevel(BTNode* root,int k) {
assert(k > 0);
if (root == NULL)
return 0;
if (k == 1) {
return 1;
}
return TreeKLevel(root->left,k-1) + TreeKLevel(root->right,k-1);
}
思路解析
4.查找值为x的结点
BTNode* TreeFind(BTNode* root, int x) {
if (root == NULL)
return NULL;
if (root->val == x)
return root;
BTNode* ret = NULL;
ret = TreeFind(root->left, x);
if (ret)
return ret;
ret = TreeFind(root->right, x);
if (ret)
return ret;
return NULL;
}
思路解析
二、二叉树OJ题
二叉树的前序遍历
题目链接：OJ链接
提示：
树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100
思路解析
此题要保存节点，所以需要先获取节点个数，然后进行前序遍历，保存每一个节点值。
代码实现：
int TreeSize(struct TreeNode* root){
return root!=NULL?1+TreeSize(root->left)+TreeSize(root->right):0;
}
void PreOrder(struct TreeNode* root,int*arr,int*i){
if(root==NULL){
return;
}
arr[(*i)++]=root->val;
PreOrder(root->left,arr,i);
PreOrder(root->right,arr,i);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize){
int n=TreeSize(root);
int* arr=(int*)malloc(sizeof(int)*n);
int m=0;
PreOrder(root,arr,&m);
*returnSize=n;
return arr;
}
图例解析
二叉树的中序遍历
题目链接：OJ链接
提示：
树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100
思路解析
解题思路同上题，遍历时进行中序遍历
代码实现：
int TreeSize(struct TreeNode* root){
return root==NULL?0:1+TreeSize(root->left)+TreeSize(root->right);
}
void MidOrder(struct TreeNode* root,int*arr,int*i){
if(root==NULL)
return;
MidOrder(root->left,arr,i);
arr[(*i)++]=root->val;
MidOrder(root->right,arr,i);
}
int* inorderTraversal(struct TreeNode* root, int* returnSize){
int n=TreeSize(root);
*returnSize=n;
int*arr=(int*)malloc(sizeof(int)*n);
int m=0;
MidOrder(root,arr,&m);
return arr;
}
图例解析
二叉树的后序遍历
题目链接：OJ链接
提示：
树中节点的数目在范围 [0, 100] 内
-100 <= Node.val <= 100
思路解析
解题思路同上题，遍历时进行后序遍历
代码实现：
int TreeSize(struct TreeNode* root){
return root==NULL?0:1+TreeSize(root->left)+TreeSize(root->right);
}
void LastOrder(struct TreeNode* root,int*arr,int*i){
if(root==NULL)
return;
LastOrder(root->left,arr,i);
LastOrder(root->right,arr,i);
arr[(*i)++]=root->val;
}
int* inorderTraversal(struct TreeNode* root, int* returnSize){
int n=TreeSize(root);
*returnSize=n;
int*arr=(int*)malloc(sizeof(int)*n);
int m=0;
LastOrder(root,arr,&m);
return arr;
}
图例解析
单值二叉树
题目链接：OJ链接
提示：
给定树的节点数范围是 [1, 100]。
每个节点的值都是整数，范围为 [0, 99] 。
思路解析
遍历二叉树，并且每一个节点值都和根节点的值进行比对，如果不等于根节点的值，则不是单值树。
代码实现：
bool isUnivalTree(struct TreeNode* root){
if(root==NULL)
return true;
if(root->left && root->left->val!=root->val)
return false;
if(root->right && root->right->val!=root->val)
return false;
return isUnivalTree(root->left)&&isUnivalTree(root->right);
}
图例解析
二叉树最大深度
题目链接：OJ链接
提示：
树中节点的数量在 [0, 104] 区间内。
-100 <= Node.val <= 100
思路解析
二叉树的最大深度等价于：左右子树的最大深度 + 1
代码实现：
int maxDepth(struct TreeNode* root){
if(root==NULL)
return 0;
int leftdeep = maxDepth(root->left);
int rightdeep = maxDepth(root->right);
return (leftdeep > rightdeep)?(leftdeep+1):(rightdeep+1);
}
图例解析：
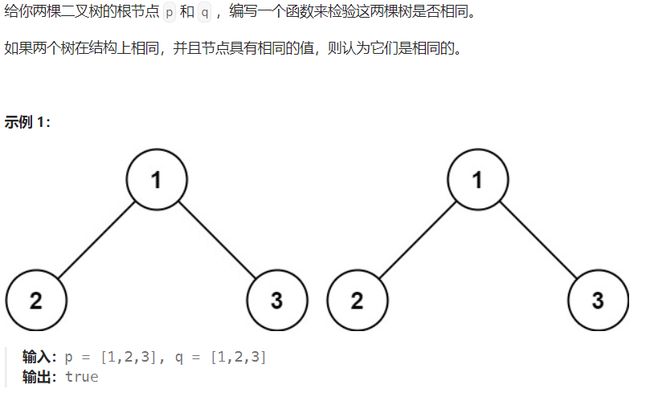
检查两颗树是否相同
题目链接：OJ链接
提示：
两棵树上的节点数目都在范围 [0, 100] 内
-104 <= Node.val <= 104
思路解析
首先比较根节点是否相同，然后分别比较左右子树是否相同
代码实现：
bool isSameTree(struct TreeNode* p, struct TreeNode* q){
if(p==NULL&&q==NULL)
return true;
if(p==NULL||q==NULL)
return false;
if(p->val!=q->val)
return false;
return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}
图例解析
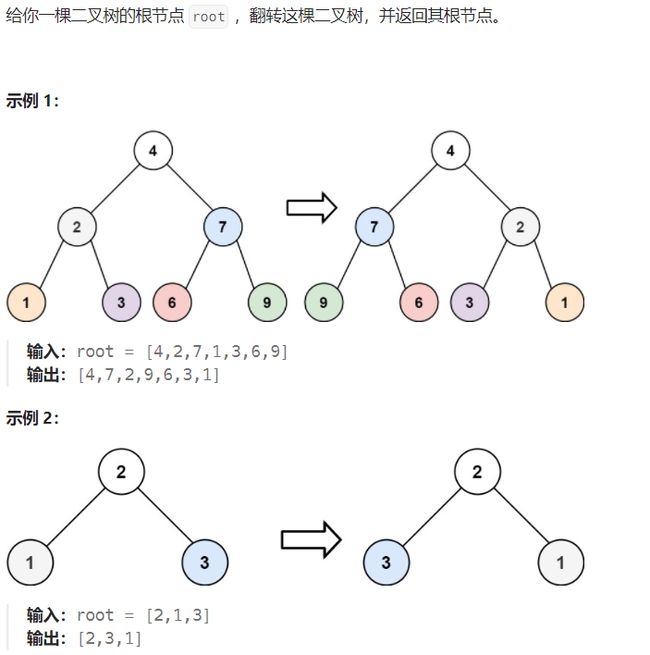
.翻转二叉树
题目链接：OJ链接
提示：
树中节点数目范围在 [0, 100] 内
-100 <= Node.val <= 100
思路解析
用后序翻转每一棵树的左右子树根节点
代码实现：
struct TreeNode* invertTree(struct TreeNode* root){
if(root==NULL) return NULL;
struct TreeNode* left=invertTree(root->left);
struct TreeNode* right=invertTree(root->right);
root->right=left;
root->left=right;
return root;
}
图例解析
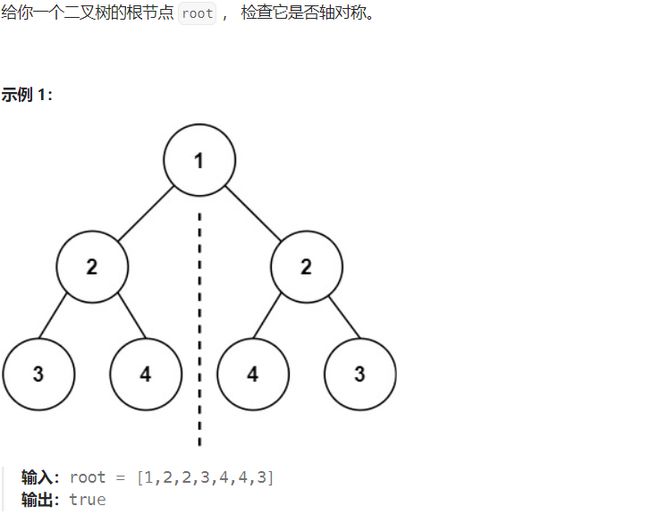
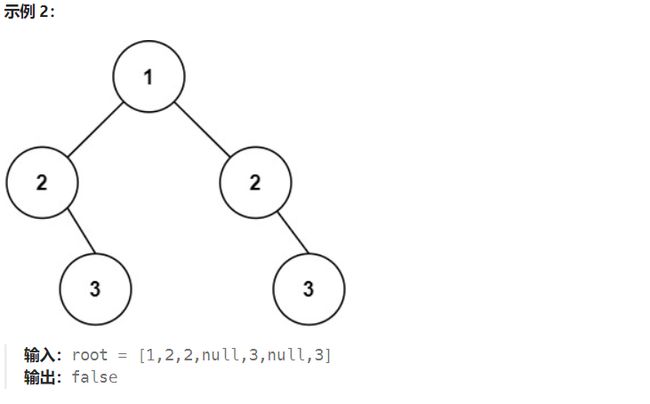
对称二叉树
题目链接：OJ链接
提示：
树中节点数目在范围 [1, 1000] 内
-100 <= Node.val <= 100
思路解析
判断一个树是否对称，首先要判断左右孩子是否对称相等，还需要判断左孩子的左子树是否和右孩子的右子树对称，左孩子的右子树是否和右孩子的左子树对称。
将左右子树传入判断二叉树是否相同的函数
代码实现：
bool check(struct TreeNode* p, struct TreeNode* q)
{
if(p == NULL && q == NULL)
return true;
if(p == NULL || q == NULL)
return false;
if(p->val == q->val)
return check(p->left, q->right) && check(p->right, q->left);
else
return false;
}
bool isSymmetric(struct TreeNode* root){
return check(root, root);
}
图例解析
具体参考前面判断二叉树是否相同的例题
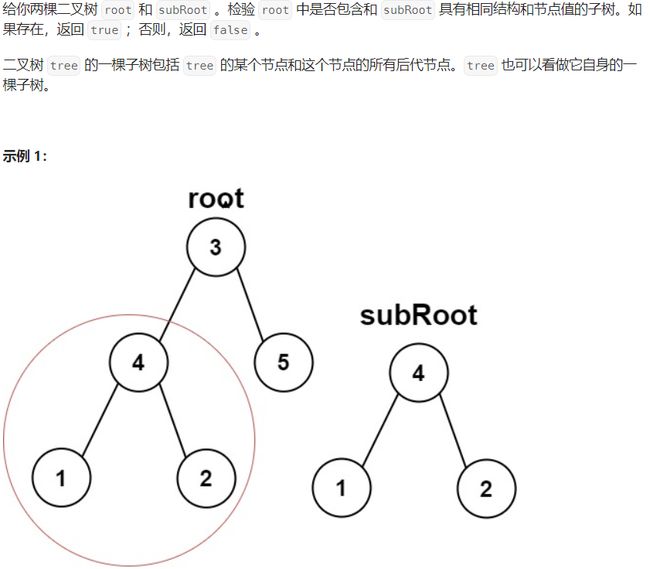
另一颗树的子树
题目链接：OJ链接
提示：
root 树上的节点数量范围是 [1, 2000]
subRoot 树上的节点数量范围是 [1, 1000]
-104 <= root.val <= 104
-104 <= subRoot.val <= 104
思路解析
判断t是否为s的子树，需要判断t是否和s的某一个子树相同，所以此题就是判断两棵树是否相同的逻辑。
前序遍历到与第二棵树根节点val相同的结点
再传入比较函数进行判断
代码实现：
bool check(struct TreeNode*p,struct TreeNode*q){
if(p==NULL&&q==NULL)
return true;
if(p==NULL||q==NULL)
return false;
if(p->val!=q->val)
return false;
return check(p->left,q->left)&&check(p->right,q->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
if(subRoot==NULL)
return true;
if(root==NULL&&subRoot==NULL)
return true;
if(root==NULL)
return false;
if(root->val==subRoot->val){
int Jb=check(root,subRoot);
if(Jb==true)
return true;
}
return isSubtree(root->left,subRoot)||isSubtree(root->right,subRoot);
}
图例解析
具体参考前面判断二叉树是否相同的例题及前序遍历例题
总结
现在我们开始一轮新的自我提升吧！
二叉树的题目当然也更有难度！
但没关系，一起加油，这些都是小困难！芜湖~