最新波士顿房价预测多元线性回归模型代码(最小二乘,岭回归,Lasso)及其数据集
一.前言
大家可以发现,网上大部分找的代码会运行报错,这是更新后的代码。最近机器学习的实验课要求做这个,本来是让GPT写,或者找别人的代码搬运过来,结果发现这个波士顿的数据集在sklearn更新中被删除了,正是因为如此,网上或者GPT都是使用sklearn的数据集所以运行报错,需要自己找数据集才能运行。故就自己学着写了。也为后续也有这个学习需求的朋友们提供这个代码来学习。需要数据集的私信我。
二.实验要求
相当于我下面展示的代码的实现功能了
1. UCI平台波士顿房价数据集准备与理解;对数据集进行可视化分析;
2.根据房价与各特征的相关性分析,选择确定影响房价的主要特征;
3.随机划分数据集,80%样本作为训练数据,20%样本作为测试数据;
4.用训练数据训练波士顿房价岭回归线性回归模型:
5.对岭回归模型进行正则参数调优;
6.测试模型在测试集上的性能,(评估指标为RMSE和R2分数)。
代码后面的注释为Lasso模型和其参数调优代码,有这部分需要可以把注释去掉运行
三.说明
3.1.需导入的库
1.pandas
2.numpy
3.matplotblib
4.sklearn(安装时使用全程:scikit-learn)
5.seaborn
全部都使用pip安装命令即可,简单快捷
win+R,输入cmd回车,pip命令【后面是镜像,不加速度非常慢】:
pip install 库名 -i https://pypi.doubanio.com/simple
3.2.数据集特征说明
数据集可私聊我发给你
涵盖了麻省波士顿不同郊区房屋14种特征的信息。本数据集共有506个样本,每个样本有13个特征及输出标签MEDV
特征信息:
CRIM 城镇人均犯罪率
ZN 占地面积超过2.5万平方英尺的住宅用地比例
INDUS 城镇非零售业务地区的比例
CHAS 查尔斯河虚拟变量 (= 1 如果土地在河边;否则是0)
NOX 一氧化氮浓度(每1000万份)
RM 平均每居民房数
AGE 在1940年之前建成的所有者占用单位的比例
DIS 与五个波士顿就业中心的加权距离
RAD 辐射状公路的可达性指数
TAX 每10,000美元的全额物业税率
PTRATIO 城镇师生比例
B 1000(Bk - 0.63)^2 其中 Bk 是城镇的黑人比例
LSTAT 人口中地位较低人群的百分数
MEDV 以1000美元计算的自有住房房价的中位数
四.代码分享
import pandas as pd
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Ridge
from sklearn.preprocessing import MinMaxScaler
from sklearn import metrics
import seaborn as sns
# 读取数据集
boston = pd.read_csv('housing.csv', header=None, delimiter=',', encoding='utf-8')
# 特征命名
boston.columns = ['CRIM',
'Z',
'INDUS',
'CHAS',
'NOX',
'RM',
'AGE',
'DIS',
'RAD',
'TAX',
'PTRATIO',
'B',
'LSTAT',
'MEDV']
# 画布属性设置
mpl.rcParams['font.family'] = ['sans-serif']
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
# 各特征与输出的散点图
plt.figure(figsize=(12, 4))
for i in range(13):
plt.subplot(1, 13, i+1)
plt.scatter(boston[boston.columns[i]], boston[boston.columns[13]], s=1)
if i == 0:
plt.ylabel('MEDV')
else:
plt.yticks([])
plt.xlabel(boston.columns[i])
plt.suptitle('各特征与输出的散点图')
plt.show()
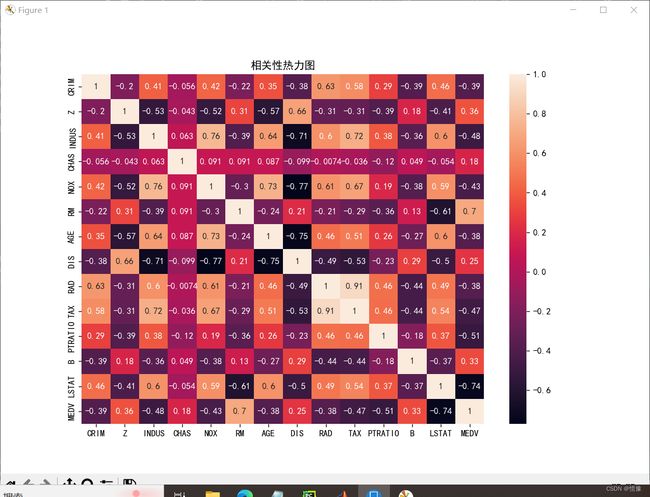
# 相关性分析图
plt.figure(figsize=(10, 7))
sns.heatmap(boston.corr(method='pearson'), annot=True)
plt.title('相关性热力图')
plt.show()
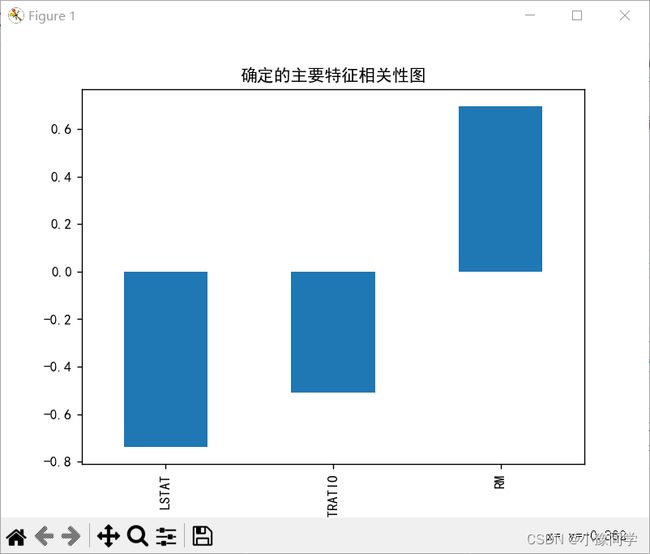
# 确定主要特征
corr = boston.corr()
corr = corr['MEDV']
corr = corr[abs(corr) > 0.5]
corr = corr[abs(corr) < 1]
corr.sort_values().plot.bar()
plt.title('确定的主要特征相关性图')
plt.show()
# 对特征进行归一化处理
scaler = MinMaxScaler()
scaler.fit(boston.iloc[:, :13])
result = pd.DataFrame(scaler.transform(boston.iloc[:, :13]))
result[13] = boston.iloc[:, 13]
boston = result
print('样本大小:', boston.shape)
# 特征再命名
boston.columns = ['CRIM',
'Z',
'INDUS',
'CHAS',
'NOX',
'RM',
'AGE',
'DIS',
'RAD',
'TAX',
'PTRATIO',
'B',
'LSTAT',
'MEDV']
# 划分特征和输出
y = boston['MEDV']
X = boston.drop(['MEDV'], axis=1)
# 划分训练数据和测试数据
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1, train_size=0.2)
# 最小二乘多元线性回归模型训练
print()
print('最小二乘')
lr = LinearRegression()
lr.fit(X_train, y_train)
print('系数:', lr.coef_)
print('偏置', lr.intercept_)
# 模型评估
y_pre = lr.predict(X_test)
MSE = metrics.mean_squared_error(y_test, y_pre)
RMSE = np.sqrt(metrics.mean_squared_error(y_test, y_pre))
R2_score = metrics.r2_score(y_test, y_pre)
print('MSE:', MSE)
print('RMSE:', RMSE)
print('R2_score:', R2_score)
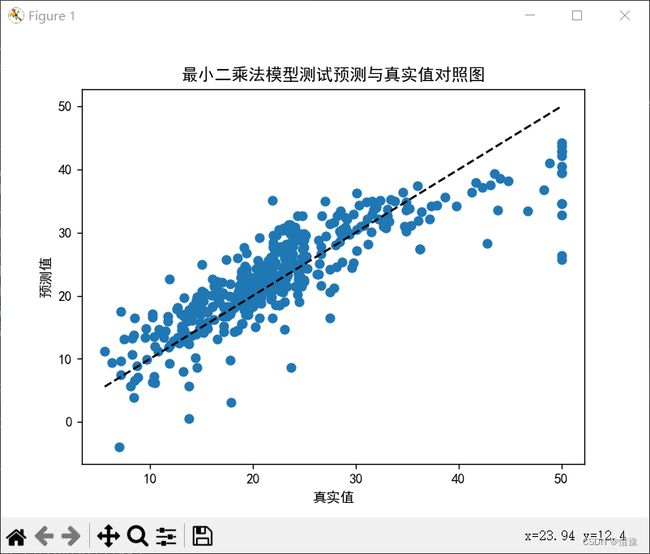
# 绘制散点图
plt.scatter(y_test, y_pre)
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'k--')
plt.xlabel('真实值')
plt.ylabel('预测值')
plt.title('最小二乘模型测试预测与真实值对照图')
plt.show()
"""
效果一遍
# 折线图
plt.figure(figsize=(15, 5))
# plt.plot(range(1, len(y_test)+1), y_test, 'bo-', range(1, len(y_test)+1), y_pre, 'ro-', linewidth=2)
plt.plot(range(1, len(y_test)+1), y_test, '-', range(1, len(y_test)+1), y_pre, '-', linewidth=2)
plt.plot(range(1, len(y_test)+1), y_test, 'o', range(1, len(y_test)+1), y_pre, 'o')
plt.title('最小二乘真实与预测图')
plt.show()
"""
# 岭回归模型
print()
print('岭回归')
ridge = Ridge()
ridge.fit(X_train, y_train)
print('系数:', ridge.coef_)
print('偏置', ridge.intercept_)
# 岭回归模型评估
y_pre = ridge.predict(X_test)
MSE = metrics.mean_squared_error(y_test, y_pre)
RMSE = np.sqrt(metrics.mean_squared_error(y_test, y_pre)) # 可以直接用MSE的函数改参数实现
R2_score = metrics.r2_score(y_test, y_pre)
print('MSE:', MSE)
print('RMSE:', RMSE)
print('R2_score:', R2_score)
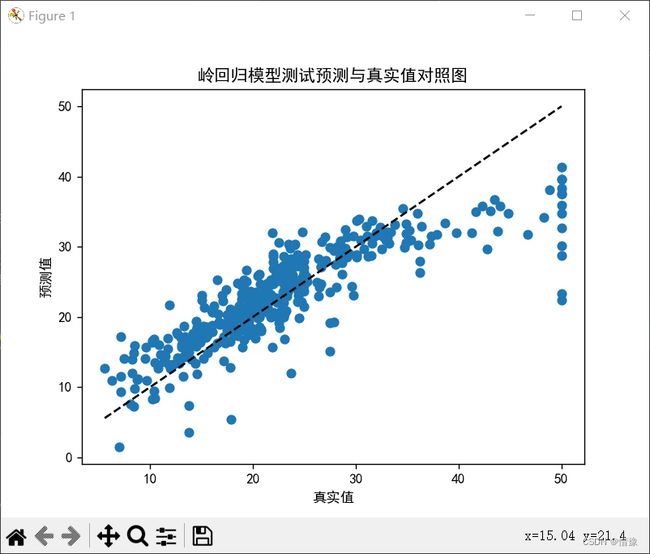
# 绘制散点图
plt.scatter(y_test, y_pre)
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'k--')
plt.xlabel('真实值')
plt.ylabel('预测值')
plt.title('岭回归模型测试预测与真实值对照图')
plt.show()
# 岭回归正则参数调优
print()
print('岭回归正则参数调优')
alpha_list = [0.01, 0.1, 1, 10, 100]
RMSE_list = []
R2_list = []
for alpha in alpha_list:
ridge = Ridge(alpha=alpha)
ridge.fit(X_train, y_train)
y_pred = ridge.predict(X_test)
rmse = metrics.mean_squared_error(y_test, y_pred, squared=False)
r2 = metrics.r2_score(y_test, y_pred)
RMSE_list.append(rmse)
R2_list.append(r2)
print('alpha:', alpha_list)
print('RMSE:', RMSE_list)
print('R2:', R2_list)
print('可以得到将正则参数alpha从1调整为0.1更合适')
print('调整前性能:RMSE={:f}, R2={:f}'.format(RMSE_list[2], R2_list[2]))
print('调整后性能:RMSE={:f}, R2={:f}'.format(RMSE_list[1], R2_list[1]))
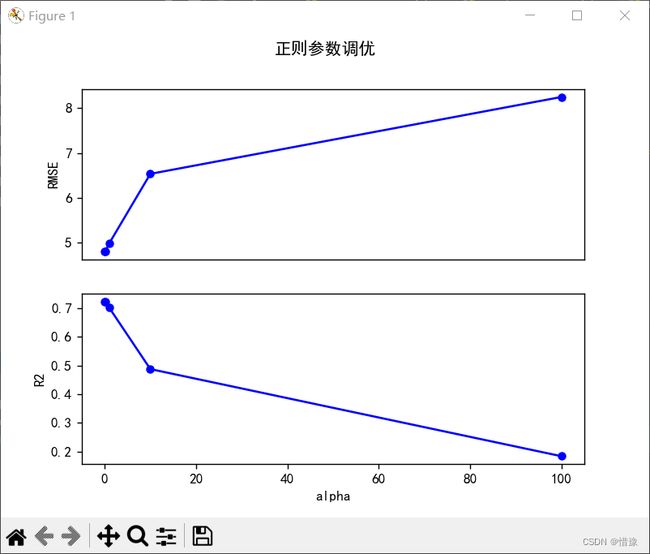
# 岭回归正则参数调优折线图
plt.subplot(2, 1, 1)
plt.plot(alpha_list, RMSE_list, 'bo-', ms=5)
plt.ylabel('RMSE')
plt.xticks([])
plt.subplot(2, 1, 2)
plt.plot(alpha_list, R2_list, 'bo-', ms=5)
plt.ylabel('R2')
plt.xlabel('alpha')
plt.suptitle('岭回归正则参数调优')
plt.show()
"""
from sklearn.linear_model import Lasso
# Lasso模型
print()
print('Lasso')
lasso = Lasso()
lasso.fit(X_train, y_train)
print('系数:', lasso.coef_)
print('偏置', lasso.intercept_)
# Lasso模型评估
y_pre = lasso.predict(X_test)
MSE = metrics.mean_squared_error(y_test, y_pre)
RMSE = np.sqrt(metrics.mean_squared_error(y_test, y_pre)) # 可以直接用MSE的函数改参数实现
R2_score = metrics.r2_score(y_test, y_pre)
print('MSE:', MSE)
print('RMSE:', RMSE)
print('R2_score:', R2_score)
# 绘制散点图
plt.scatter(y_test, y_pre)
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'k--')
plt.xlabel('真实值')
plt.ylabel('预测值')
plt.title('Lasso模型测试预测与真实值对照图')
plt.show()
# Lasso正则参数调优
print()
print('Lasso正则参数调优')
alpha_list = [0.01, 0.1, 1, 10, 100]
RMSE_list = []
R2_list = []
for alpha in alpha_list:
lasso = Lasso(alpha=alpha)
lasso.fit(X_train, y_train)
y_pred = lasso.predict(X_test)
rmse = metrics.mean_squared_error(y_test, y_pred, squared=False)
r2 = metrics.r2_score(y_test, y_pred)
RMSE_list.append(rmse)
R2_list.append(r2)
print('alpha:', alpha_list)
print('RMSE:', RMSE_list)
print('R2:', R2_list)
print('可以得到将正则参数alpha从1调整为0.01更合适RMSE,R2为:', RMSE_list[0], R2_list[0])
# lasso正则参数调优折线图
plt.subplot(2, 1, 1)
plt.plot(alpha_list, RMSE_list, 'bo-', ms=5)
plt.ylabel('RMSE')
plt.xticks([])
plt.subplot(2, 1, 2)
plt.plot(alpha_list, R2_list, 'bo-', ms=5)
plt.ylabel('R2')
plt.xlabel('alpha')
plt.suptitle('lasso正则参数调优')
plt.show()
"""
五.输出展示
样本大小: (506, 14)
最小二乘
系数: [ -9.8755277 5.59525865 4.14767959 1.6233694 -12.29434464
16.41045356 3.82938836 -14.44203599 6.93493148 -6.31195581
-11.59100667 2.57403552 -21.99545288]
偏置 29.124498484633552
MSE: 23.18366218707428
RMSE: 4.814941555935469
R2_score: 0.7219648298245814岭回归
系数: [ -4.40426752 3.27677039 -0.25610959 1.84368041 -6.66796621
14.4636706 1.87857767 -6.84278236 3.31742697 -3.32550522
-9.77131087 1.93973214 -16.36225905]
偏置 27.054675381148773
MSE: 24.884296700813074
RMSE: 4.988416251758976
R2_score: 0.701569596206263岭回归正则参数调优
alpha: [0.01, 0.1, 1, 10, 100]
RMSE: [4.812476417902067, 4.800421565883646, 4.988416251758976, 6.537167494378781, 8.250563816442893]
R2: [0.72224945202051, 0.7236391931560011, 0.701569596206263, 0.4874963995664999, 0.18363392034708204]
可以得到将正则参数alpha从1调整为0.1更合适
调整前性能:RMSE=4.988416, R2=0.701570
调整后性能:RMSE=4.800422, R2=0.723639
六.后言
代码还有些地方待优化,但问题不大,懒得改了。嘿嘿
七.更新
23/5/18添加了特征说明,更新了代码,优化后可视化表现更好,输出数据清晰,多了确定主要特征并且展示的图表。并且加了Lasso模型及其参数调优的部分(以注释形式,取消注释就能运行多这部分了)