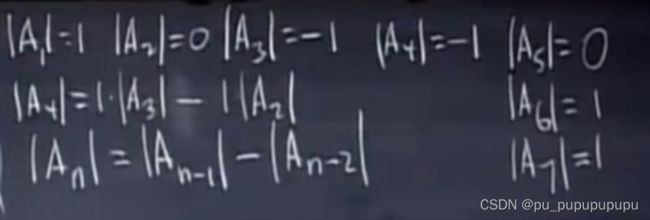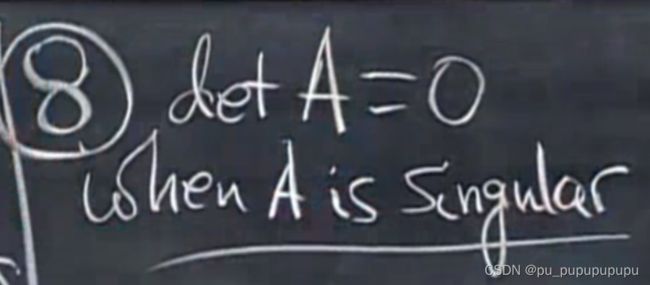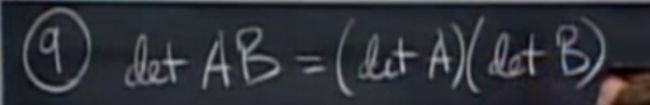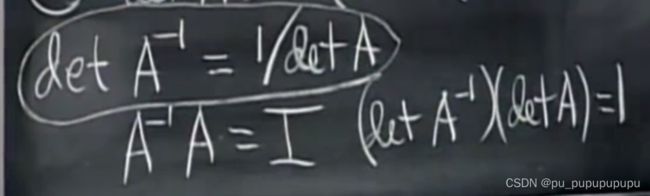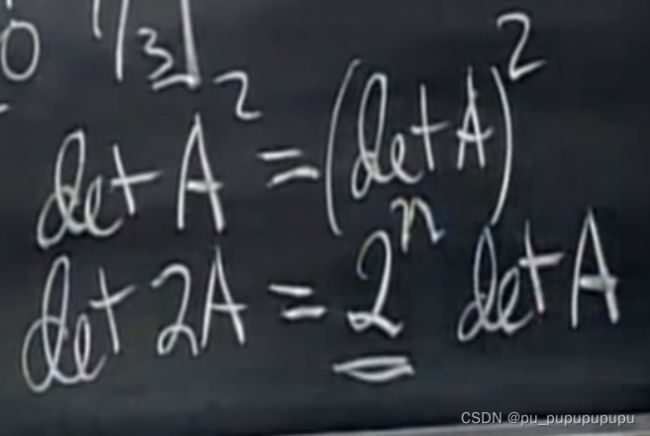线性代数基础9--正交矩阵与行列式基础,代数余子式

1,正交基与正交矩阵
标准正交向量组中,向量之间满足两两正交,并且每个基的长度为1

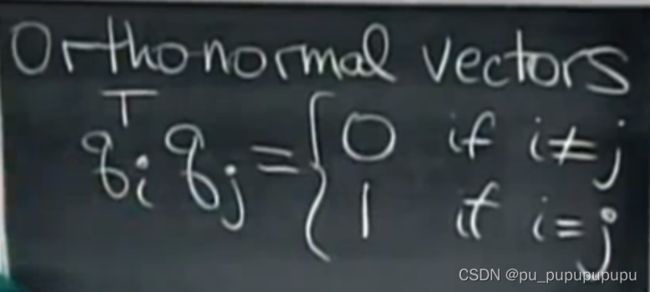
将标准正交向量组成一个矩阵Q.则有一个重要的性质,并且不要求Q一定为方阵.如下

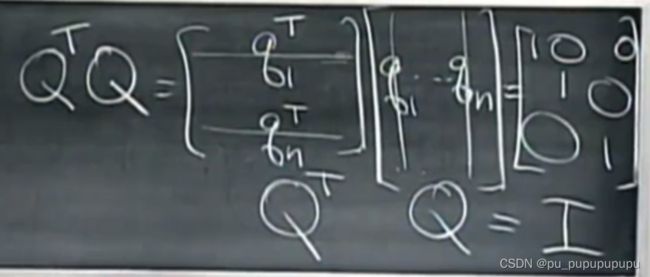
这里我们将标准正交矩阵,并且只有在Q为方阵的情况下才,简称为正交矩阵.
强调方阵是因为可逆

也许有一个问题是正交矩阵是否可逆,但是正交矩阵符合可逆的定义,我们还找出了它的可逆矩阵,(如果这两个矩阵乘积为单位矩阵,并且是方阵,那么它们互为可逆),所以Q一定可逆,也就可以说明,正交向量一定线性无关.是可以证明的,有兴趣可以网上查看.也可以简单的从正交向量几何意义解释,两个向量垂直当然除了0没有组合可以让其结果为0向量

这里有一个注意的点,一般只有方阵才考虑逆矩阵

Q的例子



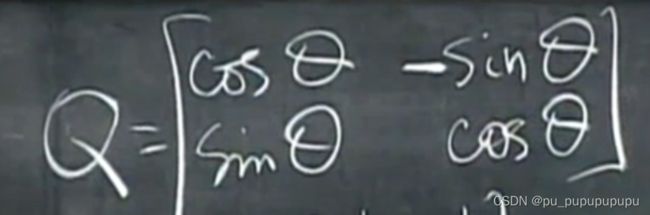
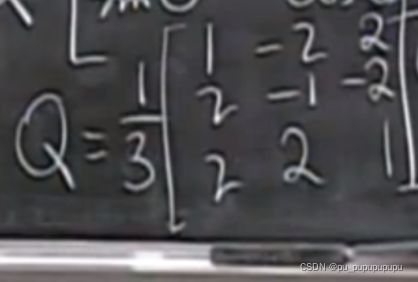
那么求得Q矩阵有什么用处呢?

前一种情况是当Q不是方阵时,只满足Q的转置×Q=I,所以投影矩阵只能化为
Q×Q的转置,因为左乘右称是不同的,而如果Q为方阵,那么就可以求Q的逆,逆左乘右乘都是一样的.所以结果可以写成I

并且满足P的两条性质:对称与投影两次与投影一次结果相同.

第二个好处:正规方程变得简单

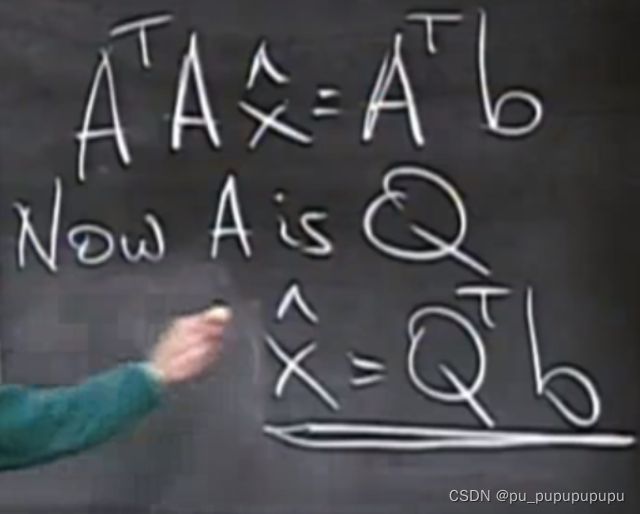
2,施密特正交法

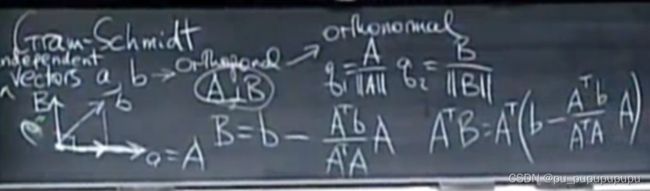
这个方法可以将几个线性无关的向量转化为对应得正交向量.
第一个向量不需要改变,只需要将第二个向量B减去B在A方向得投影.这样就得到了施密特正交法.可以看出这里的投影公式用的就是之前投影到一维的公式.
另外,如何验证两个向量正交,就是A转置×B等于0.

下面是三个向量的公式.

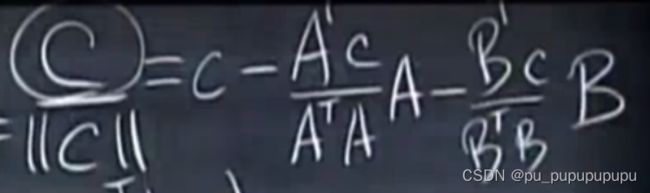
很简单,只需要将第三个向量,减去A,B两个方向的投影就好.

例子

完整的施密特正交化过程如上,a,b必须线性无关.

注意A与Q的列空间是一样的.只不过是得到相互垂直的两个基,将原本两个不正交的基转化为正交基.在一个空间中也有无数组正交基.

3,从矩阵角度看施密特分解.
A=QR

注意,这里a1转置×q2为0,因为施密特正交化就是为了找到q向量然后与原向量垂直,所以点乘为0.

4,之前学习的很多方面,都是长方矩阵,并不限定为方阵,之后将更多讨论方阵.
首先为行列式
我们学习行列式的一个重要原因是求特征值.
行列式记为

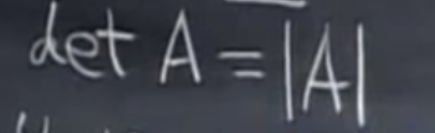
首先这个行列式是一个数,用一个数来表示一个矩阵.
这个数包含了矩阵的一些信息,最重要的就是:行列式非0,矩阵可逆

下面介绍行列式,三个基本性质

交换一行就在行列式前添加一个-号

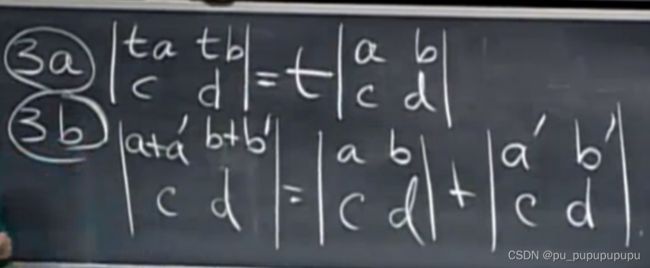
这个3b的性质表示第一行符合线性,而不是整体符合线性.如下:

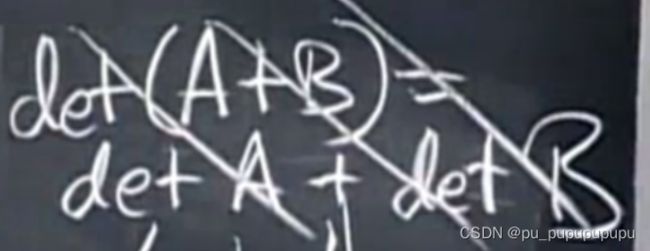
注意这个等式是错的,因为每一行都会加上b,而不是只有一行加b.

从以上的三条性质我们可以推出更多的性质.

性质4,两列相等则行列式为0.
用交换变符号性质得以证明.
并且性质4也与秩可以联系起来

性质5,一行减去另一行的任意倍数,行列式保持不变
证明如下:由于性质3和4,所以的以证明

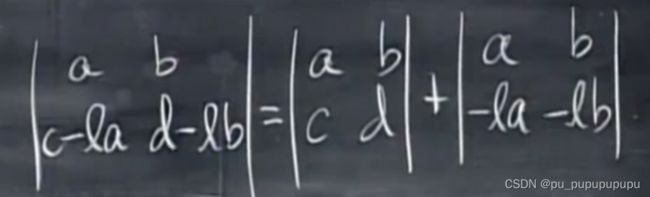
性质6,如果有一行为0行,那么行列式值为0.
证明如下:

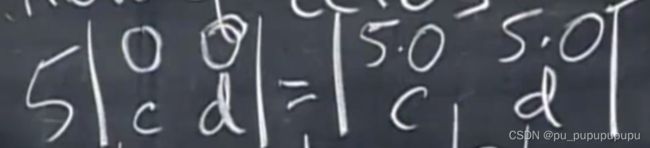
性质7,上三角行列式的值等于主元相同.

最简单的证明就是,如果主元都不等于0,那么就可以继续化简上三角行列式,变成只有对角线有数字的行列式,然后将主元提取出去(3a),再用性质1就可以得到,

性质8,

A的行列式=0,当且仅当A为奇异矩阵.即不可逆.

性质9,

引出一个重要结论

性质10,

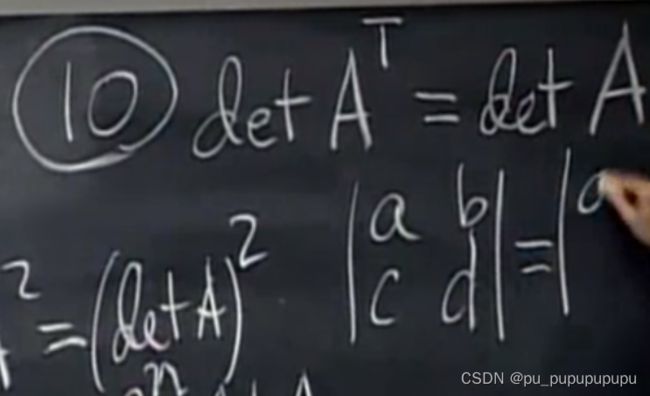
这样就解放了行和列,之前对行的性质对列也同样成立.

证明如下

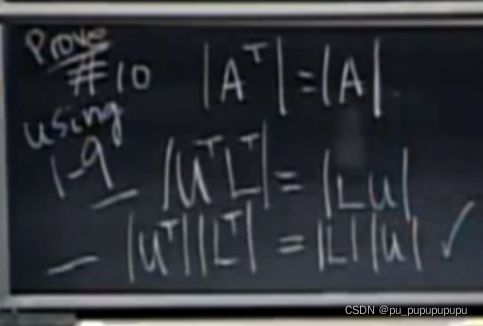
L的行列式为1,因为他是下三角矩阵并且主元都为1,同理L的转置的行列式也为1.并且U也为上三角矩阵,所以转置之后的行列式也等于主元相乘.

5,行列式公式及代数余子式
首先得到二阶行列式公式,

这种方法求行列式,会得到很多值为0的行列式,那么那些行列式值为0呢?
其实就是不同行不同列的三个元素组成的矩阵

由此,我们推导一下,行列式计算的一般公式.

如上就表示了从不同行,不同列取元素相乘,每行每列只保留一个元素,那么还有一个问题,每一项符号如何确定.

如图将列排列写出来,看经过几次交换可以得到正常顺序.

代数余子式:
如下图,将三阶行列式分解为三个两阶行列式,注意代数余子式包括正负号.


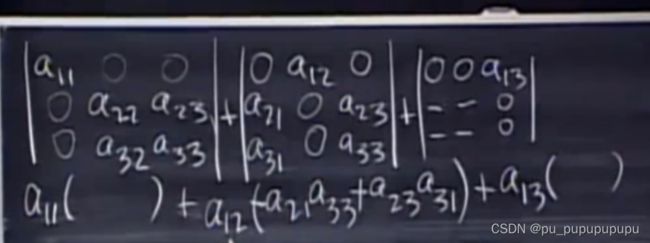
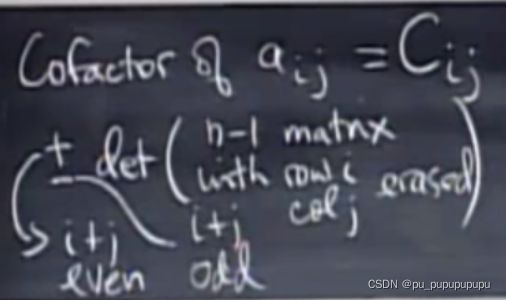
这样我们得到代数余子式的定义:将n阶行列式按一行展开,每一个元素对应一个代数余子式,Cij,它的符号为(-1)的i+j次方,它的大小为,原行列式去掉第i行,去掉第j列得到的n-1阶行列式.
所以说,如果按第二行展开,第一个元素符号就是(-1)的三次方.
如果不算符号,那么叫做余子式.

按第一行展开,公式如下:

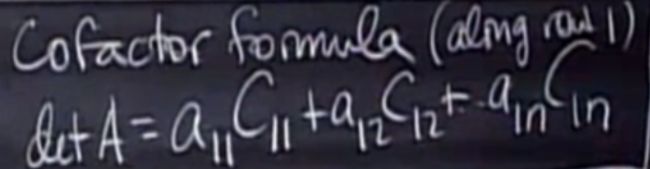
6,已知的求行列式方法
(1),将行列式化简为三角矩阵,然后主元相乘
(2),代数余子式公式

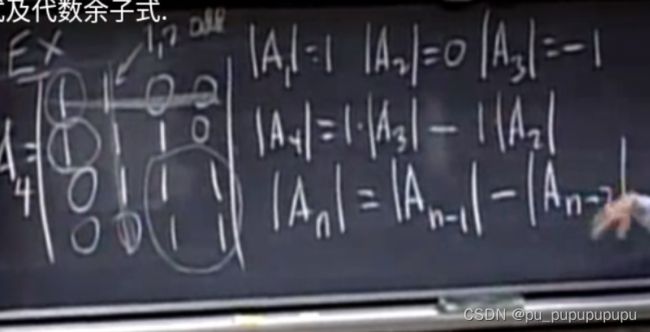
这里的A1,A2,A3,A4叫主子式.
注意这个规律只针对本行列式有用.并且其实是周期变化的.这个行列式叫三对角线行列式.