第八章 排序
一、插入排序
- 不带哨兵
void InsertSort(int A[], int n){
int i, j, temp;
for (i=1; i<n; i++){
if (A[i]<A[i-1]){
temp = A[i];
for (j=i-1; j>=0 && A[j]>temp; --j){
A[j+1] = A[j];
}
A[j+1] = temp;
}
}
}
- 带哨兵
void InsertSort(int A[], int n){
int i, j;
for (i=2; i<=n; i++){
if (A[i]<A[i-1]){
A[0] = A[i];
for (j=i-1; A[0]<A[j]; --j){ // 不用每次循环都判断j>=0
A[j+1] = A[j];
}
A[j+1] = A[0];
}
}
}
- 折半插入排序
void InsertSort(ing A[], int n){ int i, j, low, high, mid; for (i=2; i<=n; i++){ A[0] = A[i]; low = 1; high = i-1; while (low<=high){ mid = (high+low)/2; if (A[mid]>A[0]) high = mid - 1; else low = mid + 1; } for (j=i-1; j>=high+1; --j){ A[j+1] = A[j]; } A[high+1] = A[0]; } }
二、 希尔排序
思想:先追求表中元素部分有序,再逐渐逼近全局有序
这里的A[0]只是暂存单元,不是哨兵(循环语句中会判断若j<=0就到了插入位置)
void ShellSort(int A[], int n){
int d, i, j;
for (d=n/2; d>=1; d=d/2)
for (i=d+1; i<=n; ++i)
if (A[i]<A[i-d]{
A[0] = A[i];
for (j=i-d; j>0 && A[0]<A[j]; i-=d)
A[j+d] = A[j]; // 同组的记录后移,找寻当前元素的插入位置
A[j+d] = A[0];
}
}
三、冒泡排序
每一趟都能使最小的元素被放在最终位置(也可以改动以下代码使每一趟把最大的元素被放在最终位置)
void swap(int &a, int &b){
int temp = a;
a = b;
b = temp;
}
void BubbleSort(int A[], int n){
for (int i=0; i<n-1; i++){
bool flag = false;
for (int j=n-1; j>i; j--)
if (A[j-1]>A[j]){
swap(A[j-1], A[j]);
flag = true;
}
if (flag==false)
return;
}
}
四、快速排序
void QuickSort(int A[], int low, int high){
if (low<high){
int pivotpos = Partition(A, low, high);
QuickSort(A, low, pivotpos-1);
QuickSort(A, pivotpos+1, high);
}
}
int Partition(int A[], int low, int high){
int pivot = A[low];
while (low<high){
while (low<high&&A[high]>=pivot) --high;
A[low] = A[high];
while (low<high&&A[low]<=pivot) ++low;
A[high] = A[low];
}
A[low] = pivot;
return low;
}
五、简单选择排序(属于选择排序)
每一趟在待排序元素中选取关键字最小的元素加入有序子序列(即有序子序列放在整个序列的开头,每一趟找到的最小元素放在有序子序列的末尾)
void SelectSort(int A[], int n){
for (int i=0; i<n-1; i++){
int min = i;
for (int j=i+1; i<n; j++){
if (A[j]<A[min])
min = j;
}
if (min!=i)
swap(A[i], A[min]);
}
}
void swap(int &a, int &b){
int temp = a;
a = b;
b = temp;
}
六、堆排序(属于选择排序)
先建堆,再排序。建堆时让编号 ≤ n 2 \le\frac{n}{2} ≤2n的所有节点依次下坠(自底向上调整各分支节点),下坠规则就是小元素与关键字更大的孩子交换位置。排序时让堆顶元素加入有序子序列(大根堆排序时是让堆顶元素与堆底元素交换),堆底元素换到堆顶后,进行下坠调整,恢复大根堆的特性。将排序过程重复n-1趟
- 大根堆
- 建立大根堆(A[0]初始值为空)
void BuildMaxHeap(int A[], int len){ for (int i=len/2; i>0; i--) // 从后向前调整所有非终端节点 HeadAdjust(A, i, len); } // 将以k为根的子树调整为大根堆(即小元素下坠过程) void HeadAdjust(int A[], int k, int len){ A[0] = A[k]; // A[0]的作用为暂存子树根节点(即要下坠的那个小元素) for (int i=2*k; i<=len; i*2){ // 让i先指向当前节点左孩子 if (i<len && A[i]<A[i+1]) i++; if (A[0]>=A[i]) break; else{ A[k] = A[i]; k = i; } } A[k] = A[0]; }这里有个常考考点:若一个节点有两个孩子,则其“下坠”一层,需要对比关键字两次(孩子对比选最大,该节点再与大孩子对比);若下方只有一个孩子,则“下坠”一层只需对比关键字1次
- 基于建立的大根堆,进行堆排序:每一趟将堆顶元素加入有序子序列(即有序子序列放在整个序列的结尾,每一趟找到的最大元素放在有序子序列的开头),并将待排序元素再次调整为大根堆(又进行一轮小元素不断下坠)
void HeapSort(int A[], int len){ BuildMaxHeap(A, len); for (int i=len; i>1; i--){ swap(A[i], A[1]; HeadAdjust(A, 1, i-1); } }
- 建立大根堆(A[0]初始值为空)
七、归并排序
归并即把两个或多个已经有序的序列合并成一个
int *B = (int *)malloc(n*sizeof(int)); // 辅助数组B
void Merge(int A[], int low, int mid, int high){
int i, j, k;
for (k=low; k<=high; k++)
B[k] = A[k]; // 将A中所有元素复制到B中
for (i=low, j=mid+1, k=i; i<=mid&&j<=high; k++){
if (B[i]<=B[j])
A[k] = B[i++];
else
A[k] = B[j++];
}
while (i<=mid)
A[k++] = B[i++];
while (j<=high)
A[k++] = B[j++];
}
void MergeSort(int A[], int low, int high){
if (low<high){
int mid = (low+high)/2;
MergeSort(A, low, mid); // 对左半部分归并排序
MergeSort(A, mid+1, high); // 对右半部分归并排序
Merge(A, low, mid, high); // 归并
}
}
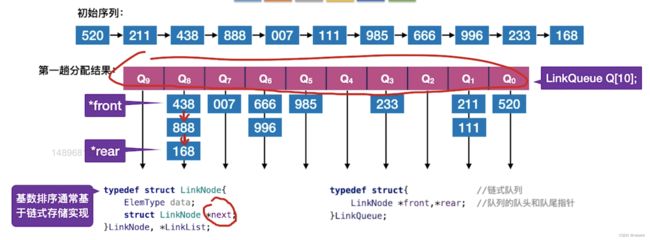
八、基数排序
基数排序不是基于比较的排序算法
只考手动模拟,几乎不考代码
- 基数排序擅长解决的问题
- 数据元素的关键字可以方便地拆分为d组,且d较小
- 每组关键字的取值范围不大,即r较小
- 数据元素个数n较大
- 基数排序通常基于链式存储实现:
- 定义包含r个队列元素的数组,每个队列保存两个指针(*front和*rear),每个队列中的元素包含数据和指向下一个元素的指针
typedef struct LinkNode{ ElemType data; struct LinkNode *next; } LinkNode, *LinkList; typedef struct{ LinkNode *front, *rear; } LinkQueue;
- 定义包含r个队列元素的数组,每个队列保存两个指针(*front和*rear),每个队列中的元素包含数据和指向下一个元素的指针
九、外部排序
- 败者树:
- 解决的问题:使用多路平衡归并可减少归并趟数,但用老土方法从k个归并段选出一个最小/最大元素需要对比关键字k-1次,构造败者树可以使关键字对比次数减少到 ⌈ l o g 2 k ⌉ \lceil log_2k \rceil ⌈log2k⌉
- 败者树可视为一棵完全二叉树(多了一个头头)。k个叶节点分别对应k个归并段中当前参加比较的元素,非叶子节点用来记忆左右子树中的“失败者”,而让胜者往上继续进行比较,一直到根节点
- 置换-选择排序:
算法效率
| 算法 | 空间复杂度 | 时间复杂度 | 算法稳定性 | 适用性 |
|---|---|---|---|---|
| 插入排序 | O ( 1 ) O(1) O(1) | 最好 O ( n ) O(n) O(n);最坏 O ( n 2 ) O(n^2) O(n2);平均 O ( n 2 ) O(n^2) O(n2) (主要来自对比关键字、移动元素,若有n个元素,需要n-1趟处理) | 稳定 | |
| 折半插入排序 | O ( 1 ) O(1) O(1) | 最好 O ( n l o g 2 n ) O(nlog_2n) O(nlog2n);最坏 O ( n 2 ) O(n^2) O(n2);平均 O ( n 2 ) O(n^2) O(n2) | 稳定 | |
| 希尔排序 | O ( 1 ) O(1) O(1) | 最坏 O ( n 2 ) O(n^2) O(n2) | 不稳定 | 仅适用于顺序表,不适用于链表 |
| 冒泡排序 | O ( 1 ) O(1) O(1) | 最好 O ( n ) O(n) O(n)(有序);最坏 O ( n 2 ) O(n^2) O(n2)(逆序);平均 O ( n 2 ) O(n^2) O(n2) | 稳定 | 适用于顺序表和链表 |
| 快速排序 | 最好 O ( l o g 2 n ) O(log_2n) O(log2n);最坏 O ( n ) O(n) O(n) | 最好 O ( n l o g 2 n ) O(nlog_2n) O(nlog2n)(每次选的pivot都能将序列分成均匀的两部分);最坏 O ( n 2 ) O(n^2) O(n2)(初始有序或逆序);平均 O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) | 不稳定 | 适用于顺序表,不适用于链表 |
| 简单选择排序 | O ( 1 ) O(1) O(1) | O ( n 2 ) O(n^2) O(n2) | 不稳定 | 顺序表、链表都可以 |
| 堆排序 | O ( 1 ) O(1) O(1) | 建堆 O ( n ) O(n) O(n)、排序 O ( n l o g 2 n ) O(nlog_2n) O(nlog2n),总时间复杂度 O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) | 不稳定 | |
| 归并排序 | O ( 1 ) O(1) O(1) | 每一趟的对比次数 O ( n ) O(n) O(n)、趟数 O ( l o g 2 n ) O(log_2n) O(log2n),总时间复杂度 O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) | 稳定 | |
| 基数排序 | O ( r ) O(r) O(r) | O ( d ( n + r ) ) O(d(n+r)) O(d(n+r)),其中数据元素的关键字拆分为d组,每组关键字的取值范围为r,数据元素个数为n | 稳定 |