计算电动力学程序设计----运动带电粒子的势和辐射场

The potential and radiation field of moving charged particles

电动力学理论

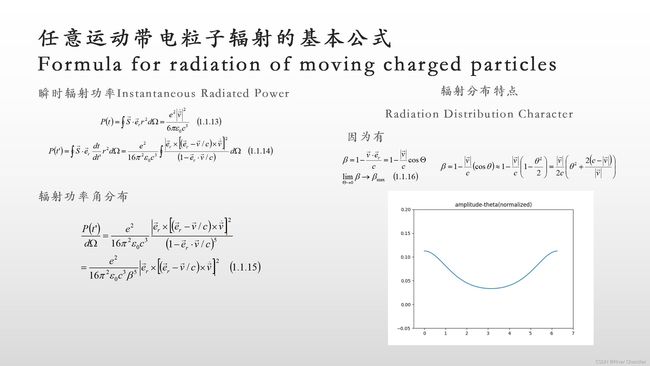
运动带电粒子辐射的基本公式

        运动带电粒子辐射的基本公式

        相关应用

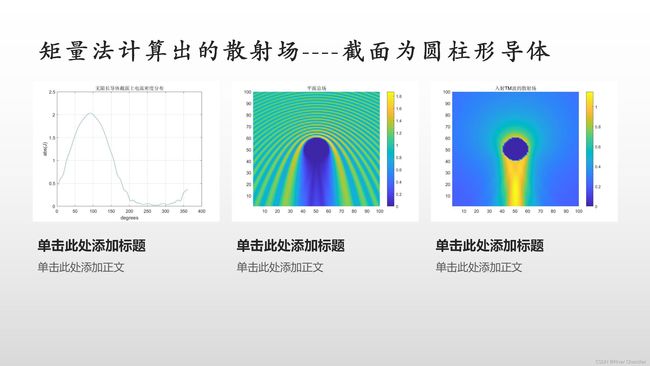
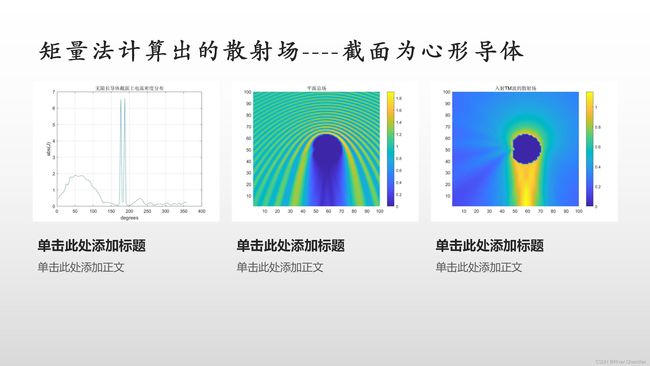
计算辐射场*

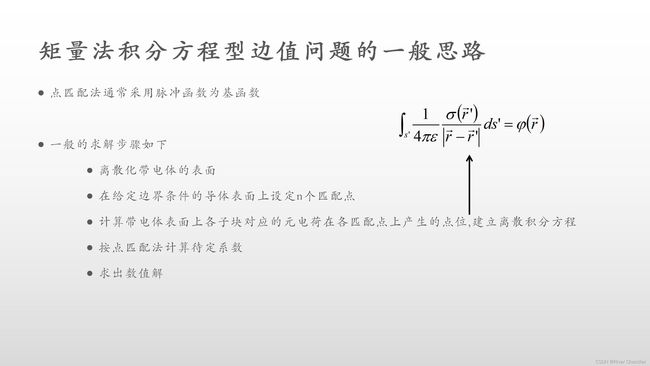
矩量法

电磁质量和辐射阻尼

        带电粒子的受力计算，能量分析，电磁质量，辐射阻尼，辐射阻尼力公式的修正

介质对电磁波的散射

        散射的定义，自由电子对电磁波的散射，束缚电子对电磁波的散射

介质对电磁波的色散和吸收

        物理模型，求解步骤，电磁波的色散和吸收

1.对粒子的力全部来自辐射场，固有场对粒子的合力为零

2.“惯性力”对应的等效电磁质量为(W0/c2) 的4/3 倍

3.辐射阻尼力与按辐射能－机械能守恒定理推出的结果一致，但此地为瞬时值而非平均值，也不要求粒子作周期运动

        当粒子从一个匀速运动状态进入另一个匀速运动状态，外界克服辐射场对粒子的惯性力做功，转换为磁能；

        电磁能增量；对匀加速运动粒子，辐射阻尼力为零,即后两项代数和为零，辐射能由系统电磁能提供

平面波、TE(M)波、TE(M)极化、极化

TEM波，即横电磁波

TE(M)极化

        如果平面波的电场分量与入射面垂直，则称平面波TE极化（S偏振光）

        如果平面波的电场分量与入射面平行，则称平面波为TM极化（P偏振光）

Python 利用矩量法实现计算电磁学的例子

        （波）极化

                波的极化分为线极化、圆极化、椭圆极化

        TE(M)波

                如果波在传播方向上没有电场分量，则为TE波；

                如果没有磁场分量，则为TM波;

                如果电场、磁场分量都没有，则为TEM波。

矩形带电导体板

# width 2b
b = 0.5
# length 2a
a = 0.5
# potential
varphi = 1
#Vacuum dielelctric constant
epr = 8.85*10**(-12)


import numpy as np
import matplotlib.pyplot as plt

Nx = 20
Ny = 20
assert(Nx==Ny),"Nx not equal Ny"

x1 = -0.475
y1 = -0.475

zx = np.array([(i/Nx-0.5*(Nx+1)/Nx)*2*a for i in range(1,1+Nx)])
zy = np.array([(i/Ny-0.5*(Ny+1)/Ny)*2*b for i in range(1,1+Ny)])

P = np.zeros((Nx,Ny))
for i in range(Nx):
    P[i][i] = 3.545*((2*a/Nx)*(2*b/Ny))**0.5
    for j in range(Ny):
        if i!=j:
            P[i][j] = (2*a/Nx)*(2*b/Ny)/((zx[i]-zx[j])**2+(zy[i]-zy[j])**2)**0.5

G = np.zeros((Nx,1))
for i in range(Nx):
    G[i][0] = 4*np.pi*epr*varphi

一维带电导体棒

#IS the system of units
#radius a
a = 0.001
#length L
L = 1
#Vacuum dielelctric constant
epr = 8.85*10**(-12)
#potential
varphi = 100


import numpy as np
import matplotlib.pyplot as plt

#Discrete field source point
N = 20
z1 = -0.475
z = np.array([(i/N-0.5*(N+1)/N)*L for i in range(1,N+1)])

#set LEFT
LEFT = np.zeros((N,N))
for i in range(N):
    LEFT[i][i] = 2*np.log(2/N/a)
    for j in range(N):
        if i != j:
            LEFT[i][j] = L/N/(a**2+(z[i]-z[j])**2)**0.5

#set RIGHT
RIGHT = np.zeros((N,1))
for i in range(N):
    RIGHT[i][0] = 4*np.pi*epr*varphi

SOLVE = np.linalg.solve(LEFT,RIGHT)

plt.ylim(0,max(SOLVE)*1.25)
plt.plot(z,SOLVE,label="potential")
plt.xlabel("x")
plt.ylabel("charge")
plt.pause(0.02)

---

课程演示计算程序

电动力学演示

import numpy as np
import matplotlib.pyplot as plt

c = 3e8
v = 0.2*c
a = 0.1*v

#k = e^2/(16*pi^2*erpsilon*c^3)

theta = np.arange(0,2*np.pi,0.01*np.pi)
##beta = (1-v/c*np.cos(theta))**(-5)*((1-v/c*np.cos(theta))*a)**2
##beta = beta/(sum(beta**2))**0.5


##beta = a**2*np.sin(theta)**2/(1-v/c*np.cos(theta))**5
##beta = beta/(sum(beta**2))**0.5

Phi = np.arange(0,np.pi/2+np.pi/14,np.pi/14)
for phi in Phi:
    beta = ((1-v/c*np.cos(theta))**2-(1-v**2/c**2)*np.sin(theta)**2*np.cos(phi)**2)/(1-v/c*np.cos(theta))**5
    beta = beta/(sum(beta**2))**0.5
    plt.plot(theta,beta,label="phi="+str(round(phi,2)))


plt.title("Power-theta(normalized)")
plt.legend()
plt.pause(0.02)

矢量可视化

import math
import time
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D  # 空间三维画图
import numpy as np

x,y,z=[0,2,1],[0,2,2],[0,5,2]
u,v,w=[1,2,1],[1,1,1],[3,1,1]



fig = plt.figure()
ax = Axes3D(fig)
arrow = ax.quiver(x, y, z, u, v, w, length=0.1, normalize=False)
# plt.show() # don't use this sentence and it shall work
##for i in range(100):
##    print(i)
##    plt.cla() # plt.clf()
##    u = math.cos(math.pi / 6 * i)
##    v = math.sin(math.pi / 6 * i)
##    arrow = ax.quiver(x, y, z, u, v, w, length=0.1, normalize=True)
##    plt.draw()
##    plt.pause(.001)
ax.quiver(x, y, z, u, v, w, length=0.1, normalize=True)
plt.pause(.001)

矢量可视化案例

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 定义三维矢量场
def vector_field(x, y, z):
    dx = np.sin(x) * np.cos(y)
    dy = np.sin(x) * np.sin(y)
    dz = np.cos(x)
    return dx, dy, dz

# 生成网格点
x, y, z = np.meshgrid(np.linspace(-1, 1, 10), np.linspace(-1, 1, 10), np.linspace(-1, 1, 10))

# 计算矢量场
vx, vy, vz = vector_field(x, y, z)

# 绘制矢量场

fig = plt.figure()
ax = fig.gca(projection='3d')
ax.set_xlim(-2.5,2.5)
ax.set_ylim(-2.5,2.5)
ax.set_zlim(-2.5,2.5)
ax.quiver(x, y, z, vx, vy, vz)
plt.show()

参考文献

[1]运动带电粒子的势和辐射场

[2]原子物理学[M]·杨福家

[3]量子电动力学[M]·栗弗席茨

[4]计算电磁学[M]·金建铭

[5]拉普拉斯变换及其应用[J]·符云锦

2023春季学期学习报告

• 本征值问题的数值解法
  • 正方向，反方向相交法
  • 有限元方法
  • 有限差分法
• 一维谐振子
  • 解中心势场为一维谐振子势下的薛定谔方程
• Woods-Saxon
  • 解中心势场为一维谐振子势下的薛定谔方程
• Matlab Pdetool
• 有限差分矩阵法
• 国家级大学生创新创业训练计划
• 美国大学生数学建模竞赛