【论文笔记】Optimal trajectory generation for dynamic street scenarios in a Frenét Frame

经典Frenet坐标系横纵向解耦优化规划的方法。
由于个人能力所限，可能有所纰漏，还请批评指正，希望和大家共同学习。

Abstract

• 提出了一种semi-reactive的轨迹生成算法，可以很好得集成进行为决策层。该方法通过基于Frenet坐标系中的最优控制策略来将被动碰撞和定速巡航、并道、跟车等进行结合。
• 在无约束优化问题的最优解集合中寻找合理的近似来解决受约束的优化问题，并选择最佳解决方案，以满足约束条件。
• 高速横纵向互相解耦；低速则不同。

I. INTRODUCTION

A. Motivation

传统的算法存在一些局限性，难以适用于动态复杂的环境以及高速场景。而作者提出的方法能够：

1. 很好的适应于公路场景，并且能够生成保持 速度不变（指变道、并道等操作与行驶速度独立） 的驾驶动作以及将速度和距离控制传递给规划层面。
2. 通过结合转向、制动/加速来实现reactive(被动?)的障碍物避障。

B. Related work

• [11], [19], [2], [4]: 使用一个连接起点和一个远的可能的目标状态的全局轨迹，但这类方法没有考虑自动驾驶车辆行车过程中各类不确定性，依赖于其他交通参与者的未来行为轨迹的精准预测。
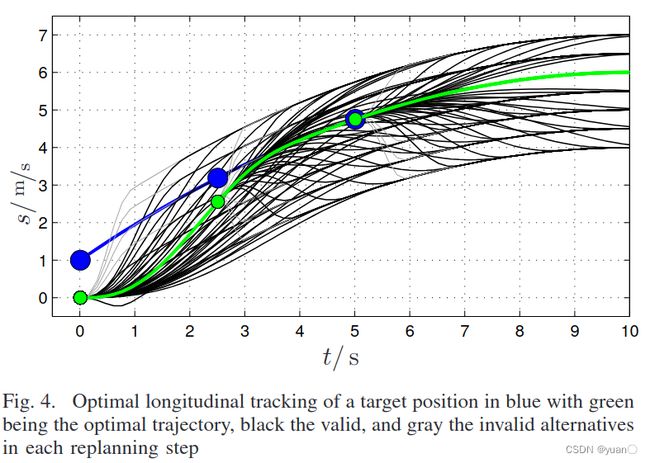
• [16], [1], [7]:使用了离散优化的方法：通过对车辆动力学微分方程的前向积分来获得有限轨迹库(控制空间的离散化)。利用轨迹库，使用cost函数进行评价、打分，作局部路径规划。轨迹的类型可以有很多种形式。但是，这种方式可能会非最优。而且这种方式可能会产生超调甚至不稳定性,如下图所示。
  
  这张图说明重规划频率高的轨迹可以避免或减少重规划频率低的轨迹所遇到的超调甚至是不稳定问题。

PS1：类似的论文Maximum Likelihood Path Planning for Fast Aerial Maneuvers and Collision Avoidance Ji Zhang, Chen Hu, Rushat Gupta Chadha, and Sanjiv Singh
PS2：之前移动机器人运动规划课程的笔记：https://blog.csdn.net/sinat_52032317/article/details/132125557

• [9]: 通过RRT模拟闭环系统对轨迹树进行采样[10] .
• [17]：与本文类似的思想，但没有考虑障碍物。提到了Galerkin base这个概念。

PS:Galerkin base:Galerkin基是一种基函数，可以在函数空间中描述一个系统的动态行为。在优化控制中，使用Galerkin基来表示系统的状态和控制空间，以便找到最优的控制轨迹。简单来说，Galerkin基是一种数学方法，用于将一个系统的动态行为表示为一组基函数的线性组合，从而简化系统的建模和控制。

PS：Bellman最优性原理是动态规划的基本原则之一。该原理指出，在任何情况下，决策的最优序列都包含着当前决策的最优决策序列。也就是说，如果我们在一个问题中找到了最优决策序列，则这个序列中的每个决策都是这个问题的最优决策，无论之前的决策序列如何。这个原理是动态规划算法的基础，将复杂问题逐步分解为简单问题，并进行逐步求解。

II. OPTIMAL CONTROL APPROACH

作者使用在轨迹生成中引入最优控制的思想，用以保证轨迹的时间一致性。

---

Q：通常来说，采用代价函数的方式可能不会遵守Bellman最优性原理，在下一次规划的时候，规划出的轨迹会有不同。那么本文是如何做到的呢？

A：本文的方法符合Bellman最优性原理，是因为在轨迹生成过程中，将轨迹跟踪问题优化为最优控制问题，并选择一个符合最优性原理的代价函数。最优性原理指的是，当一个最优解被找到后，它将一直被保留，直到问题的某些方面发生变化。在我们的方法中，一旦找到了最优解，车辆就会在每个规划步骤中沿着预先计算的轨迹的剩余部分行驶，从而保证了轨迹的时间一致性。 轨迹的时间一致性在后面的图中会直观展示。

---

• 在最优控制方面，主要是遵循Bellman的最优化原则去选取cost
  function，轨迹在最小化cost的基础上也能最大程度的接近车辆理想的开车形式。

  理想的自动驾驶车辆运动行为：在偏离车道后，能够很好地平衡舒适度(用$jerk$衡量)以及回到期望位置的时间($t_{end}-t_{start}$)。

• 在解决一般受限制的优化问题时，由于问题不限于某个函数类，因此问题变得非常复杂，最多只能进行数值求解。因此，作者提出的方法是在无约束（free）优化问题的最优解集合中寻找合理的近似来解决受约束的优化问题，并选择最佳解决方案，以满足约束条件。这意味着一旦找到最佳解决方案是有效的（约束条件不再活跃），non-reactive轨迹的时间一致性就得到保证。

  简单来说，就是用无约束优化问题下求得的最优解序列去近似受约束的优化问题。

III. MOTION PLANNING IN THE FREN ́ET FRAME

轨迹跟踪控制里比较好的方法是Frenet坐标系方法，能在

• $SE(2):=SO(2)\times {\mathbb{R}}^2$特殊欧式子群里有很好的跟踪性能(invariant tracking
  performance)

  PS:特殊欧式子群SO(2)是指二维旋转群，它由所有二维旋转矩阵组成，形式为： S O ( 2 ) = { ( cos ⁡ ( θ ) − sin ⁡ ( θ ) sin ⁡ ( θ ) cos ⁡ ( θ ) )   |   θ ∈ [ 0 , 2 π ) } SO(2) = \left\{ \begin{pmatrix} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{pmatrix} \:\middle|\: \theta \in [0, 2\pi) \right\} SO(2)={(cos(θ)sin(θ)​−sin(θ)cos(θ)​) ​θ∈[0,2π)} 其中$\theta$表示旋转角度。
  特殊欧式子群SE(2)是指二维欧氏群，它由所有二维刚体运动矩阵组成，包括平移和旋转，形式为： S E ( 2 ) = { ( cos ⁡ ( θ ) − sin ⁡ ( θ ) x sin ⁡ ( θ ) cos ⁡ ( θ ) y 0 0 1 )   |   θ ∈ [ 0 , 2 π ) , x , y ∈ R } SE(2) = \left\{ \begin{pmatrix} \cos(\theta) & -\sin(\theta) & x \\ \sin(\theta) & \cos(\theta) & y \\ 0 & 0 & 1 \end{pmatrix} \:\middle|\: \theta \in [0, 2\pi), x, y \in \mathbb{R} \right\} SE(2)=⎩ ⎨ ⎧​ ​cos(θ)sin(θ)0​−sin(θ)cos(θ)0​xy1​ ​ ​θ∈[0,2π),x,y∈R⎭ ⎬ ⎫​
  其中$\theta$表示旋转角度，$x$和$y$表示平移量。二维欧氏群是非常重要的，因为它是机器人和计算机视觉等领域中常见的运动群，可以用于描述机器人在平面上的运动。

• Frenet坐标系下的规划问题中，参考线十分重要。参考线可以是道路中心线、或者是非结构化道路下path planning产生的粗轨迹。
  基于动态参考系分别生成横纵向上的1维轨迹。相对关系如下所示：$$x(s(t),d(t))=r(s(t))+d(t)n_r(s(t))$$$r$是center line上的参考点；$d(t)$为横向偏差；$s(t)$是指沿着center
  line的方向一段时间经过的弧长；$t_x,n_x$分别是轨迹的切向和法向向量。

本文采用五次多项式作为轨迹，可以达到minimum jerk的效果，构建了经典的BVP/OBVP问题。之前相关的笔记：https://blog.csdn.net/sinat_52032317/article/details/132125557

$$J_t(p(t)):={\int }_{t_0}^{t_1}{\ddot{p}}^2(\tau )\mathrm{d}\tau .$$
起点状态：$P_0=[p_0,{\dot{p}}_0,{\ddot{p}}_0]$，起点时间$t_0$；
终点状态：$P_1=[{\dot{p}}_1,{\ddot{p}}_1]$，终点时间$t_1=t_0+T$;

代价函数是一个五次多项式：
$$C=k_j{J}_t+k_{t}g(T)+k_{p}h(p_1)$$
其中 $g$和 $h$是任意的函数，$k_j,k_t,k_p$>0
看一下论文的证明过程(证明代价函数$C$也是五次多项式)：
反证法：
若不是，则$J_t$始终会比五次多项式的形式要小。

IV. GENERATION OF LATERAL MOVEMENT

PS：在最优控制领域中，“目标流形”是一个术语，它指的是在控制系统中，控制输入所需达到的状态变量集合。在优化控制问题中，目标流形是优化问题的一部分，它描述了系统必须遵循的约束条件。在论文中，作者将${\dot{d}}_1=d_1=0$作为目标流形，以便汽车沿着中心线平行移动。

A. High Speed Trajectories

高速时采用横纵向解耦，独立计算的方式。

起始状态由前一段轨迹计算得到，从而保证连续性：$D_0=[d_0,{\dot{d}}_0,{\ddot{d}}_0]$。为了使轨迹平行于center line，终末状态${\dot{d}}_1,=0{\ddot{d}}_1=0$。再另$g(T)=T,h(d_1)=d_1^2$（前者为了加速收敛，后者为了减小与center line的偏离）,得到最后的代价函数:
$$C_d=k_j{J}_t(d(t))+k_{t}T+k_d{d}_1^2,$$

结合下图来阐述一下轨迹生成的流程。

第一步：不是直接计算出轨迹，再调整相关参数。作者首先生成了一个轨迹库，包含终末状态$d_i$以及经历时间$T_j$:
$$[d_1,{\dot{d}}_1,{\ddot{d}}_1,T{]}_{ij}=[d_i,0,0,T_j]$$

第二步：选出最低代价有效轨迹。

每个周期规划出来的轨迹会沿着上一个周期规划出来的最优轨迹继续规划。这样就能够符合Bellman最优性原理以及达到时间一致性。

B. Low Speed Trajectories

对于低速场景，横纵向解耦的方式忽略了车辆的非完整性约束，所以轨迹可能不有效。低速时的相对关系如下所示：
$$x(s(t),d(t))=r(s(t))+d(s(t))n_r(s(t)).$$为什么高速场景下不也这么做呢？

对于低速场景，可以在behavioral层设置一个速度阈值，当速度低于这个阈值时基于纵向运动生成横向轨迹。

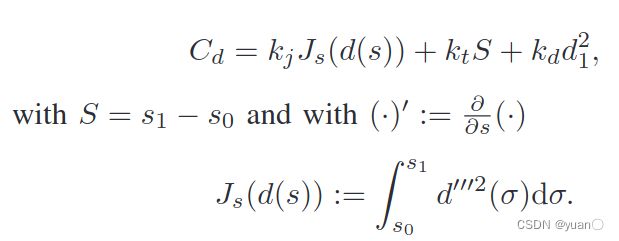
低速场景下的代价函数。
轨迹库的生成和高速情况类似，但是要注意$d^{{}^{\prime }}$是对$s$求导
$$[d_1,{\dot{d}}_1,{\ddot{d}}_1,T{]}_{ij}=[d_i,0,0,T_j]$$

V. GENERATION OF LONGITUDINAL MOVEMENT

横向规划主要将时间/距离作为主要的评判标准，此处的评判标注主要是comfort和safety，所以引入了纵向的jerk 作为优化问题的考虑。

结合图理解纵向规划的过程。

对于跟车、并道以及停车等场景，需要有一个目标状态$s_{target}(t)$作为引导，再在每一次的周期中，更新末端约束(会有不同的$\Delta s_i$以及$T_j$)。
$S_0=[s_0,{\dot{s}}_0,{\ddot{s}}_0]$
$$[s_1,{\dot{s}}_1,{\ddot{s}}_1,T{]}_{ij}=[[s_{\text{target}}(T_j)+\Delta s_i],{\dot{s}}_{\text{target}}(T_j),{\ddot{s}}_{\text{target}}(T_j),T_j]$$
代价函数为：$C_t=k_j{J}_t+k_{t}T+k_s[s_1-s_d{]}^2.$

Following

提到了constant time gap law

PS:“constant time gap law"是指国际交通规则中要求车辆与前车保持一定时间间隔的安全距离，该距离会随着速度的变化而变化。这个时间间隔被认为是一个常数，因此被称为"constant time gap law”。这个规则的目的是确保在高速公路等高速道路上行驶的车辆之间保持安全距离，以确保行车安全。

$$s_{\mathrm{target}}(t):=s_{lv}(t)-[D_0+\tau {\dot{s}}_{lv}(t)]$$

$D_0,\tau$是固定的；$s_{lv},{\dot{s}}_{lv}$分别是前车的位置与速度。
其中前车的一些数据都是需要通过感知预测来获得的，其中我们假设前车的加速度保持不变，${\ddot{s}}_{lv}(t)={\ddot{s}}_{lv}\left(t_0\right)=const.$对时间积分可得：

$$\begin{array}{rl}{\dot{s}}_{lv}(t)& ={\dot{s}}_{lv}(t_0)+{\ddot{s}}_{lv}(t_0)[t-t_0]\\ s_{lv}(t)& =s_{lv}(t_0)+{\dot{s}}_{lv}(t_0)[t-t_0]+\frac{1}{2}{\ddot{s}}_{lv}(t_0)[t-t_0{]}^2,\end{array}$$

然后再得到目标状态的剩余变量。
$$\begin{array}{rl}{\dot{s}}_{\mathrm{target}}(t)& ={\dot{s}}_{lv}(t)-\tau {\ddot{s}}_{lv}(t),\\ {\ddot{s}}_{\mathrm{target}}(t)& ={\ddot{s}}_{lv}(t_1)-\tau {\ddot{s}}_{lv}(t)={\ddot{s}}_{lv}(t_1).\end{array}$$

Merging and Stopping

$$s_{\mathrm{target}}(t)=\frac{1}{2}[s_a(t)+s_b(t)]$$
并道的目标点定在两车之间。
停车场景则是如下：$s_{\mathrm{target}}=s_{\mathrm{stop}},{\dot{s}}_{\mathrm{target}}\equiv 0,{\ddot{s}}_{\mathrm{target}}\equiv 0.$

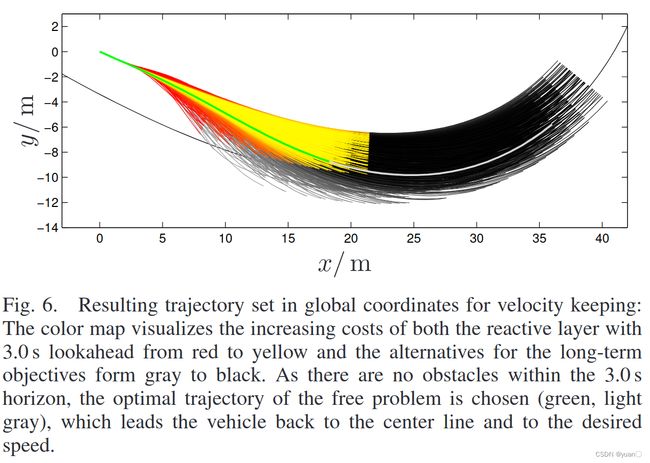
Velocity Keeping

针对前方无车的情况，代价函数如下：$C_v=k_j{J}_t(s(t))+k_{t}T+k_{\dot{s}}[{\dot{s}}_1-{\dot{s}}_d{]}^2$
通过用$\Delta \dot{s}，T_j$来改变终末状态的约束，来生成四次多项式的轨迹库：$[{\dot{s}}_1,{\ddot{s}}_1,T{]}_{ij}=[[{\dot{s}}_d+\Delta {\dot{s}}_i],0,T_j]$

VI. COMBINING LATERAL AND LONGITUDINAL TRAJECTORIES

• 先对轨迹进行加速度限幅检查，再进行合并。

• 通常情况下，参考线不是close
  form的，而是由预先采样得到的点集进行表示(航向角${\theta }_r(s)$,曲率${\kappa }_r(s)$，曲率的导数${\dot{\kappa }}_r(s)$),无法用数值求解的方式得到更高阶的信息。

  PS: close form是一个数学概念，指的是可以用有限的基本算术运算和函数运算，以及有限次求导和积分等基本数学运算得到的解析式表示的数学表达式。

• 最后轨迹的联合代价通过给横纵向添加不同的权重系数得到：$C_{tot}=k_{lat}{C}_{lat}+k_{lon}{C}_{lat}$

• 减少不必要的side-pass的措施：碰撞检查的范围随着时间扩张一点点。

• 当遇到需要变更参考线的情况时，需要将终末端点$(x,{\theta }_x,{\kappa }_x,v_x,a_x)$投影到新的参考线上的起点$[s_0,{\dot{s}}_0,{\ddot{s}}_0,d_0,{\dot{d}}_0,{\ddot{d}}_0]$.$s_0$除外，因为没有限定特定的参考线形状。但是可以通过构建优化的问题进行求解。$s=\underset{\sigma }{\mathrm{argmin}}\Vert x-r(\sigma )\Vert$

图中轨迹颜色的变化代表了cost的变化。

VIII. EXPERIMENTS

Fig. 7. Simulated highway scenario: The center line is given by the middle lane and the desired speed is significantly higher than the traffic flow. Two completely reactive passing maneuvers are shown between t = 0.0 s and 7.75 s, as well as between t = 29.07 s and 50.0 s with predicted obstacle movements on Thor ≤ 3.0 s.

TRANSFORMATIONS FROM FREN ́ET COORDINATES TO GLOBAL COORDINATES

这篇论文的附录也是挺有用的，介绍了从Frenet到全局坐标的变换。

进一步了解可以参考这篇博客。Frenet坐标系及其与笛卡尔坐标转换(1)原理

代码

[1] https://atsushisakai.github.io/PythonRobotics/modules/path_planning/path_planning.html
[2] https://github.com/ChenBohan/Robotics-Path-Planning-04-Quintic-Polynomial-Solver/blob/master/Optimal%20Trajectory%20in%20a%20Frenet%20Frame/cubic_spline_planner.py
[3] https://github.com/AtsushiSakai/PythonRobotics/tree/master/PathPlanning
[4] https://github.com/ndrplz/self-driving-car/blob/master/project_11_path_planning/src/coords_transform.h
[5] https://github.com/caokaifa/Matlab-planning
[6] https://github.com/AtsushiSakai/PythonRobotics/blob/master/PathPlanning/FrenetOptimalTrajectory/frenet_optimal_trajectory.py
[7] https://www.cnblogs.com/kin-zhang/p/15006838.html