【论文笔记】NeRF-Det: Learning Geometry-Aware Volumetric Representation for Multi-View 3D Object Detection

原文链接：https://arxiv.org/abs/2307.14620

1. 引言

  深度传感器在室内场景中（如VR、AR设备上）很少被使用，因此仅依赖相机进行3D目标检测充满挑战。最直接的几何建模方法是估计深度，但单目深度估计算法不能准确估计深度且不能实现多视图一致性。
  神经辐射场（NeRF）被证明能有效建模几何，但将其应用于3D目标检测比较复杂，因为

1. 渲染NeRF需要对空间的高频采样以避免混叠，但3D检测的体积网格分辨率较低。
2. 传统NeRF进行逐场景优化（即需要对每个场景训练一个NeRF），在基于图像的3D目标检测任务中会有相当大的延迟。
3. NeRF能利用多视图一致性在训练时学习几何，但简单的将NeRF和感知缝合起来（先重建后检测）不能带来多视图一致性的优势。

  本文提出NeRF-Det，显式地将场景几何建模为不透明度场，并联合训练NeRF分支和3D检测网络。具体来说，本文将射线样本投影到图像上，从高分辨率图像特征图中提取特征。为增强NeRF模型对未知场景的泛化性，本文使用更多先验增强图像特征，作为NeRF MLP的输入，使NeRF建模的特征更有区分性。与之前的文章直接缝合NeRF与感知不同，本文将NeRF分支与检测分支通过共享的MLP（用于预测密度场）连接起来，使得NeRF分支的梯度能反向传播到图像特征，有益于检测分支的训练。随后，将密度场转化为不透明度场，与均匀分布的体积网格的特征相乘，以减少体积网格特征中空空间的权重。最后，几何感知的体积网格特征被送入检测头进行检测。推断过程中，NeRF分支被移除，从而最小化了原始检测器的额外开销。
  实验表明显式地将几何建模为不透明度场，能建立更好的体积网格表达，从而大幅提高无深度测量下的性能；若训练时有深度测量，能进一步提高性能，且推断时无需深度传感器。此外，在新视图合成和深度估计上的实验表明，本文的方法能合成合理的新视图图像、进行精确的深度估计，表明了本文的3D体积网格特征能更好地表达场景几何。

3. 方法

  如图所示，NeRF-Det通过提取图像特征并投影为3D体积网格，进行基于图像的3D目标检测。使用NeRF推断场景几何，并使用共享MLP连接3D目标检测与NeRF，以使用NeRF中的多视图约束来增强几何估计。

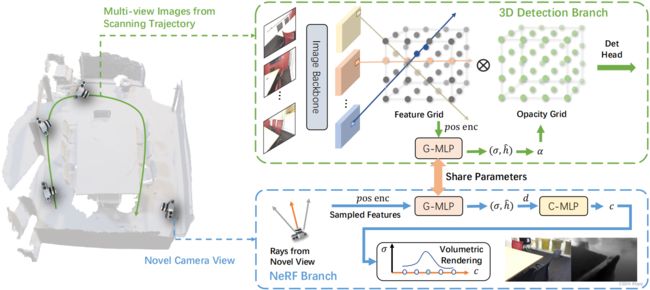
3.1 3D检测分支

  首先将多视图图像输入2D图像主干。使用FPN融合多尺度特征，并选择最高分辨率的特征生成3D体积网格。
  具体来说，在3D空间创建$N_x\times N_y\times N_z$的体素，然后将每个体素的中心投影到图像上，得到相应的像素索引。使用最近邻插值方法采样投影点附近的图像特征。对于投影到图像外部或者位于图像平面背后的点，将体素特征设置为0。然后，将多视图特征的有效体素取平均：$V^{avg}(p)={\sum }_{i=1}^{M_p}{V}_i(p)/M_p$（$M_p$为有效的2D投影数）。
  但是上述方式生成的体积网格特征没有考虑空的空间，使得3D表达是模糊的。本文提出使用NeRF分支提高检测分支学习几何的能力。

3.2 NeRF分支

  特征采样：NeRF是新视图合成使用的神经渲染方法。过去的NeRF从高分辨率3D体积网格采样特征，对低分辨率的3D检测任务而言会产生混叠。本文从高分辨率图像特征图上采样特征，如图所示。

  具体来说，首先沿从相机出发的射线$\mathbf{r}(t)=\mathbf{o}+t\times \mathbf{d}$采样点（其中$\mathbf{o}$为射线起点，$\mathbf{d}$为射线方向）。对射线上坐标$\mathbf{p}$的点而言，可按下式计算其颜色$\mathbf{c}(\mathbf{p},\mathbf{d})$和密度$\sigma (\mathbf{p})$：$$\begin{gathered} \sigma (\mathbf{p}),\hat{\mathbf{h}}(\mathbf{p})=\text{G-MLP}(\bar{V}(\mathbf{p}),\gamma (\mathbf{p})) \\ \mathbf{c}(\mathbf{p},\mathbf{d})=\text{C-MLP}(\hat{\mathbf{h}}(\mathbf{p}),\mathbf{d}) \end{gathered}$$其中$\bar{V}(\mathbf{p})$为从多视图特征聚合和增强的射线特征（见后文），$\gamma (\mathbf{p})$为位置编码，$\hat{\mathbf{h}}$为隐特征。$\text{G-MLP}$用于估计几何，而$\text{C-MLP}$用于估计颜色。对于激活函数，为密度$\sigma (\mathbf{p})$使用ReLU，而为颜色$\mathbf{c}(\mathbf{p},\mathbf{d})$使用Sigmoid。
  增强特征：上述方法不足以使G-MLP准确估计场景几何。因此，本文使用更多先验帮助优化G-MLP。首先计算来自不同视图采样特征的方差$V^{var}(p)={\sum }_{i=1}^{M_p}(V_i(p)-V^{avg}(p){)}^2/M_p$进行增强。颜色特征的方差能粗略表达3D场的占用率：如果一个3D位置$\mathbf{p}$被占用，则特征方差应该很小。
  此外，还使用RGB值进行增强采样特征（同样计算来自各视图的均值和方差）。因此，增强特征$\bar{V}$为$\{V^{avg},V^{var},RG{B}^{avg},RG{B}^{var}\}$的拼接。增强特征被通过NeRF MLP生成密度和颜色。本文使用体素渲染生成最终像素的颜色和深度：$$\hat{\mathbf{C}}=\sum _{i=1}^{N_p}{T}_i{\alpha }_i{\mathbf{c}}_i,D(r)=\sum _{i=1}^{N_p}{T}_i{\alpha }_i{t}_i$$其中$T_i=\exp (-{\sum }_{j=1}^{i-1}{\sigma }_j{\delta }_t),{\alpha }_i=1-\exp (-{\sigma }_i{\delta }_t)$，$t_i$是第$i$个采样点与相机的距离，${\delta }_t$是射线上采样点之间的距离。

3.3 估计场景几何

  本文使用不透明度场进行场景几何建模。不透明度场是一种体积网格表达，表示物体在特定区域的存在性（即如果某区域存在不能看穿的物体，该区域的不透明度场应该为1.0）。为了生成不透明度场，使用上述相同方法增强检测分支中的特征，其中G-MLP的权重是与NeRF分支共享的。这样可以使NeRF中的梯度回传到检测分支，有利训练；此外，推断时可直接将检测分支增强的体积网格特征输入G-MLP。G-MLP公式$\sigma (\mathbf{p})=\text{G-MLP}(\bar{V}(\mathbf{p}),\gamma (\mathbf{p}))$中的$\mathbf{p}$为检测分支体素的中心位置。
  随后，将密度场转化为不透明度场：$\alpha (\mathbf{p})=1-\exp (-\sigma (\mathbf{p})\times {\delta }_t)$。但此处${\delta }_t$无法获取，因为没有定义射线。不过，由于体积网格是均匀分布的，${\delta }_t$为常数，因此可以从公式中取出，得到$\alpha (\mathbf{p})=1-\exp (-\sigma (\mathbf{p}))$。最后将不透明度场与3D检测特征网格$V^{avg}$按元素相乘。

3.4 3D检测头与训练目标

  本文使用ImVoxelNet相同的检测头，对每个物体选择27个候选位置并使用3个卷积预测类别、尺寸与中心位置。
  对NeRF分支和检测分支联合训练，测试时无需对NeRF分支进行逐场景优化。检测分支使用与ImVoxelNet相同的损失，包含分类的focal损失、中心性损失和定位损失。NeRF分支使用光度损失$L_c=\Vert \hat{C}(r)-{\hat{C}}_{gt}(r){\Vert }_2$。若存在深度真值，可进一步考虑深度损失$L_d=\Vert D(r)-D_{gt}(r)\Vert$，其中$D(r)$是3.2节中最后一式的结果。网络最终的损失为上述损失之和。

4. 实验

4.1 主要结果

  定量结果：与SotA方法ImVoxelNet相比，NeRF-Det有更好的性能；使用深度监督后性能进一步提升，这说明更好的几何建模对3D检测有用。由于NeRF需要大量的迭代来优化，因此本文加倍训练轮数，得到了明显更好的性能。NeRF-Det缩小了基于RGB的方法与基于点的方法之间的性能差距。
  定性结果：可视化表明，NeRF-Det对密集场景和多尺度物体都能有有较好的检测。
  对场景几何建模的分析：本节将基于不透明度场的方法与其余的场景几何建模方法比较。
  使用深度图：假设在训练和推断阶段均可获取深度图。此时会根据深度图，仅将每个图像特征放置于唯一的体素单元中。直观来看，这样能减小体素表达的模糊性。在使用真实深度图的情况下，能确定NeRF-Det的性能上限，因为NeRF能获取完美的场景几何建模。
  在实际情况下，不能获取真实深度，因此本文使用NeuralRecon，利用边界框外的几何重建来渲染深度图。但实验表明，该方法的性能低于ImVoxelNet，表明深度估计误差增大了检测的不确定性。
  代价体积网格：计算代价体积网格的常规方法是使用源视图和参考视图之间的协方差。这与本文计算不同视图的方差类似。本文使用3D卷积编码代价体积网格，并通过Sigmoid得到概率体积网格，并与特征体积网格$V^{avg}$相乘。实验表明该方法能略微超过ImVoxelNet。
  注意本文的NeRF-Det在去掉NeRF分支后，与基于代价体积网格的方法非常类似，区别在于：（1）本文使用了平均值和颜色值增强代价体积网格中的方差值；（2）本文使用MLP和不透明度函数而非Sigmoid建模场景几何。实验表明本文的方法与基于上一段中代价体积网格的方法性能接近，且均能超过ImVoxelNet。
  使用不透明度场建模场景几何，能达到更好的性能。这表明，比起预测深度和代价体积网格，不透明度场能更有效地建模场景几何。
  与先NeRF后检测的方法比较：与NeRF-RPN相比，NeRF-Det有更好的性能，且推断时间大幅减小。此外，NeRF-RPN的高计算开销使其几乎不能在大型数据集上进行训练。
  NeRF分支能学习到场景几何吗？本文通过NeRF分支的新视图合成和深度估计来验证这一点。

4.2 消融研究

  对G-MLP与特征采样策略的消融：共享G-MLP使得多视图一致性的约束能从NeRF分支传播到检测分支。在无共享G-MLP的情况下，性能大幅下降，此时多视图一致性仅传播到图像主干。
  在共享G-MLP的情况下，从多视图图像采样特征与从体积网格采样特征，均能超过ImVoxelNet，且前者的NeRF分支和检测分支均能有更好的性能。两分支性能的正比关系表明更好的NeRF优化能导致更高的检测性能。
  对不同损失的消融研究：实验表明NeRF分支仅使用光度损失与仅使用深度损失，检测分支的性能相近，表明多视图RGB一致性足以提供学习几何的线索。无任何损失时，性能与基于代价体积网格的方法相近。
  对不同特征的消融研究：引入方差特征进行增强能大幅提高性能，表明方差特征确实能提供几何先验。此外，引入图像RGB也能提高性能，表明低级色彩也能提供几何线索。
  对检测分支影响新视图合成的消融研究：虽然NeRF能通过场景几何建模促进3D检测，但检测分支对NeRF有负面影响。这可能是检测分支会消除NeRF需要的低级细节。

A. 数据集与实施细节

  NeRF分支：训练时从10个新视图采样2048条射线作为监督信号。体积网格渲染时，若多于8个点位于空空间，则丢弃该射线，不进行损失计算。

C. 额外结果

  对视图数量的消融研究：训练时使用的视图数不变（20），测试时改变视图数，发现使用的视图增多时，性能提升显著。ImVoxelNet的提升则有限，甚至在视图数超过100时出现下降。

D. 对户外3D检测的讨论

  对户外检测而言，可能存在下列困难：难以保证运动物体的多视图一致性；无界的场景体积网格；迅速变化的光照条件（影响RGB精度）。