数据结构与算法(六)--链表的遍历,查询和修改,删除操作
一、前言
上篇文章我们了解了链表的概念以及链表底层的搭建以及向链表中添加元素的操作。本次我们继续学习链表剩余的操作:遍历,查询和修改、删除操作。
二、链表查询以及遍历
①获得链表的第index(0-based)个位置的元素(不常用,仅做练习)
和add不一样的是,add我们是要找到第Index的前一个元素,所以,我们起点从dummyHead开始,然后遍历index次。而get不同,get就是要第Index上的元素,所以我们可以直接从dummyHead.next开始,其实就是"索引"为0的位置开始,遍历index次,这样就可以找到第Index个位置的元素了。
//获取index索引上的元素
public T get(int index) {
if (index < 0 || index >= size) {
throw new IllegalArgumentException("get failed;index should >= 0 or index < size");
}
Node cur = dummyHead.next;
for (int i = 0; i < index; i++) {
cur = cur.next;
}
return cur.data;
}
那么同理有了get(),我们就可以添加更方便的一些方法,例如getFirst()和getLast():
public T getFirst(){
return get(0);
}
public T getLast(){
return get(size - 1);
}
②、查找链表中是否有元素e
这个就有点特殊了,因为我们现在不知道具体要在哪个“索引”操作,所以我们需要从头开始遍历
那么我们可以使用for循环,和之前一样,从"索引"为0的位置开始找,然后遍历size次,这种方式是可行的。但是这里呢我们采用while循环来遍历链表,因为这种方式我们后面会用到很多,那么代码非常的简单,如下所示,这其实就是链表的遍历:
public boolean contains(T t){
Node cur = dummyHead.next;
//只要cur不为NULL,其实就是到最后一个节点
while (cur != null){
if(cur.data == t){
return true;
}
cur = cur.next;
}
return false;
}
其实用for循环不使用size变量也是可以做到的,思路和上面的while循环大同小异:
for(Node cur = dummyHead.next; cur != null; cur = cur.next){...}
类似的,我们也可以在toString()中去遍历我们的链表:
@Override
public String toString(){
StringBuilder stringBuilder = new StringBuilder();
Node cur = dummyHead.next;
while (cur != null){
stringBuilder.append(cur + "->");
cur = cur.next;
}
stringBuilder.append("NULL");
return stringBuilder.toString();
}
三、链表的更新(不常用,仅做练习)
更新操作其实和上面的get操作非常类似,只是将返回元素变为了直接更新,这里不做赘述,代码如下:
public void set(int index, T t){
if (index < 0 || index >= size) {
throw new IllegalArgumentException("get failed;index should >= 0 or index < size");
}
Node cur = dummyHead.next;
for (int i = 0; i < index; i++) {
cur = cur.next;
}
cur.data = t;
}
四、链表元素的删除
那么有了之前的基础,我们删除元素是很简单的,我们仍然需要用到虚拟头结点。
例如,我想要删除"索引"为2位置上的元素:

那么对于删除链表元素来说,我们和添加元素是一样的,我们需要找到被删除元素的前一个元素,所以我们仍然需要prev,而prev.next就是我们要删除的节点delNode了:
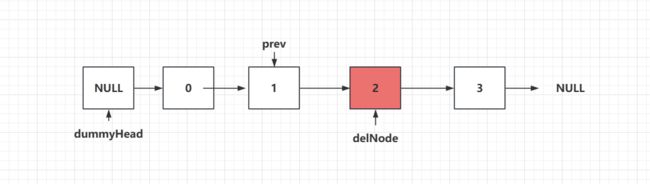
然后 我们要做的就是将prev.next = delNode.next:,这样做完之后,我们链表顺着这个next走。1的next就是3,3的next就是4,从某种意义来说等同于将2这个节点删除了。
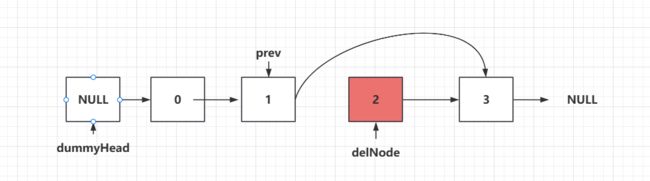
当然为了方便我们java回收这个空间,我们应该手动将2这个删除节点的next指向null,delNode.next =null;
然后我们便可以开始进行代码设计了,删除代码非常的简单:
public T remove(int index){
if (index < 0 || index >= size) {
throw new IllegalArgumentException("get failed;index should >= 0 or index < size");
}
Node prev = dummyHead;
for(int i = 0;i<index;i++){
prev = prev.next;
}
Node ret = prev.next;
prev.next = ret.next;
ret.next = null;
size --;
return ret.data;
}
那么remove完成后,我们同理可以设计一些方便的remove方法,即removeFirst,removeLast等:
public T removeFirst(){
return remove(0);
}
public T removeLast(){
return remove(size - 1);
}
我们可以试试:
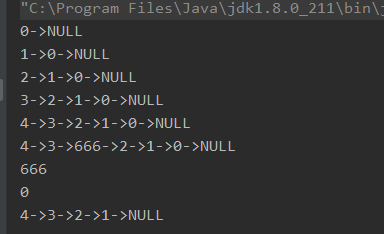
public static void main(String[] args) {
LinkedList<Integer> integerLinkedList = new LinkedList<>();
for (int i = 0; i < 5; i++) {
integerLinkedList.addFirst(i);
System.out.println(integerLinkedList);
}
integerLinkedList.add(666,2);
System.out.println(integerLinkedList);
System.out.println(integerLinkedList.remove(2));
System.out.println(integerLinkedList.removeLast());
System.out.println(integerLinkedList);
}
添加操作
- addLast(e) ----------- O(n)
- addFirst(e) ---------- O(1)
- add(index,e) -----------O(n/2)=O(n)
所以综上来看,链表的添加操作是O(n)的
删除操作
- removeLast(e) ----------- O(n)
- removeFirst(e) ---------- O(1)
- remove(index,e) -----------O(n/2)=O(n)
所以综上来看,链表的删除操作也是O(n)的
修改操作
- set(index,e) -------O(n)
查找操作
- get(index) ----------- O(n)
- contains(e) ----------- O(n)
但是如果查询的是链表头元素的时候,此时时间复杂度是O(1)
所以综上来看,链表的查找操作也是O(n)的
那么综上分析,链表的CRUD操作时间复杂度全是O(n)的,确实在时间复杂度的角度上分析,它确实整体不如数组,因为数组具有随机访问的能力,但是链表底层上就不支持。但是我们发现如果只对链表头进行增删操作,时间复杂度均为O(1),所以我们的链表它适合做的事情是不去修改,而对于查也不能去查任意的元素,可以只查链表头的元素.并且在增加和删除的时候,只能对链表头进行操作。且链表本身就是动态的数据结构,是非常节省内存空间的。