LeetCode 42 接雨水双指针

42. 接雨水

难度【困难】1170

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 感谢 Marcos 贡献此图。

示例:

输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6

---

解题方法：

第一种： 暴力法

	直接按问题描述进行。对于数组中的每个元素，我们找出下雨后水能达到的最高位置，等于两边最大高度的较小值减去当前高度的值。
	就拿上面 数组的部分 元素 为 arr = [0,1,0,2] -> index[0,1,2,3] 举例。
arr[2] 为当前元素， 寻找两边的最大值， 向左找到 最大值 left_max = 1, 向右找到最大值 right_max = 2
那么 当前元素 arr[2] 所能保存的雨水 为 min(left_max, right_max) - arr[i]  = 1
结果为 1 即保存最大雨水量 1.

代码

public static int useCommon(int[] height){
        // 使用暴力法
        /**
         * 直观想法
         * 直接按问题描述进行。对于数组中的每个元素，我们找出下雨后水能达到的最高位置，等于两边最大高度的较小值减去当前高度的值。
         */
        int n = height.length;
        int ans = 0;
        for (int i = 1; i < n - 1; i++) {
            int maxLeft=0, maxRight = 0;
            for (int j = i; j >=0 ; j--) {
                maxLeft = Math.max(maxLeft, height[j]);
            }
            for (int j = i; j < n ; j++) {
                maxRight = Math.max(maxRight, height[j]);
            }
            ans += Math.min(maxLeft, maxRight) - height[i];
        }
        return ans;
    }

第二种 使用双指针法

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-t2jQVb7r-1587867135709)(D:\hehe\剑指offer\leetcode42接雨水双指针.PNG)]

	其实 也就是 对每个元素 都能找到它当前最大的界定值， 就是暴力法中 left_max 与 right_max比较，找到个较小的。这里 left 在保证 right比他大的情况下，他才能 每走一步就敢确定 当前所能接的雨水，因为他不知道 挨着他的右边是不是闭口，即比他大，不过无所谓，因为 有right做了保证。
	9 0 0 0 0 0 10  ---> 9 的右边由10来保证。
	然后，循环里面 就是判断 当前 值和自己左边或右边的 max 比较，如果大于max 就更新，否则就判断能接多少雨水， ans += max - 当前缩印的值, ans 负责记录累加值。
	下面具体说一下每一步代码的执行流程：
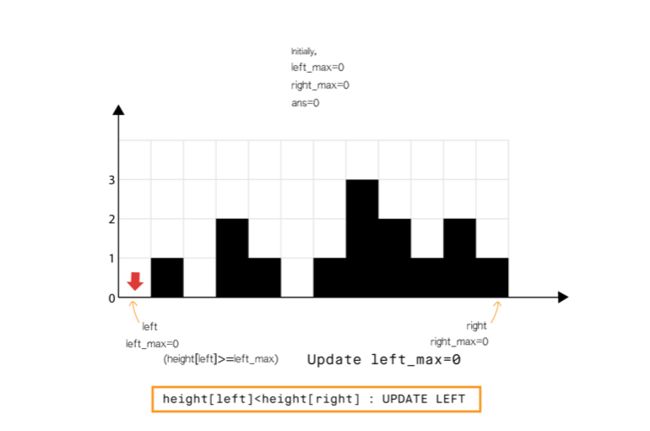
	1、先初始化 left和right , left 指向 数组 索引 0, right 指向数组 height.length - 1。
	   接着初始化 left_max = 0,right_max = 0, ans = 0. left_max表示在左边找到暂时的最大值，同理right_max表示右边的暂时最大值，ans则为累积的雨水量。
	2、然后进行遍历判断：当 left < right:
		里面再进行两个判断：
		A: 如果 左边height[left]小于右边的height[right]: 就去判断左边，先说下为什么可以去判断更小的一边，因为 更小的一边有更大的一边给他做边界保证， 比如 3... 6，左边 3 有可能盛 的雨水 3 * length_3_to_6 。继续， 
		下面进行判断： 当前值是否大于等于 现有的left_max, 如果大于就用当前值height[left]更新left_max。因为当前值比之前的left_max还大，就无法进行盛雨水了， 比如 3 ... 4 ... 6, 4 比 3 大，就不能再以 3 为左边界了，因为4 > 3， 当前4的位置 他和 3 是无法围成一个蓄水池的。 
	如果不大于，那么 就计算累积的雨水量， ans +=  (left_max - height[left]); : 举个例子  3,2...4...6,比如当前结果是 2, left_max = 3 ,也就是当前 3 - 2 = 1 即 能存 1 的雨水。 为什么不用考虑 1 后面的情况，这是因为前面说过了，有最右边的 height[left] < height[right] 作保证，保证右边界大于左边界。
		B: 左边的判断逻辑和上面的一样。

代码

public static int doublePointer(int[] height){
        // 使用双指针法
        int ans = 0,x=0,y=0;
        int left_max = 0, right_max = 0;
        int left = 0, right = height.length - 1;
        while (left < right){
            // 先判断左右哪个元素更小些 这样由小一点的那端进行界定
            if(height[left] < height[right]){
                // 判断当前值 是否是左边的最大值
                x = height[left] >= left_max ? (left_max = height[left]): (ans += (left_max - height[left]));
                ++left;
            }else {
                y = height[right] >= right_max?(right_max = height[right]):(ans+= (right_max - height[right]));
                --right;
            }
        }
        // System.out.println("x: " + x + "\n" + "y: " + y);
        return ans;
    }

参考leetcode 42 接雨水