机器学习（3） K近邻算法（KNN）介绍及C++实现

前言

        此前已发布的两篇博客，分别记录在假设空间有限、样本空间有限条件下如何计算泛化误差上界，并给出C++代码实现，详情参见机器学习（1）泛化误差上界的实现及分析；以及在线性可分条件下，采用随机梯度下降法收敛分二分类超平面的感知机算法，并给出C++代码实现，详情参见机器学习（2） 感知机原理及实现。
        感知机是基础的分类学习方法， 对于线性不可分模型、多类别分类问题束手无策。本篇博文带来一种基于实例的多分类机器学习算法，K近邻算法，K-Nearest-Neighbour(KNN)。带来K近邻算法的详细解释，讲解KD树构建过程，掌握如何实现基于KD树的最近邻查询、K近邻查询，以及如何使用K近邻查询进行投票选择生成查询样本的预测类别，并附上本文的C++代码实现。与此前的文章不同，此前文章一般等到全文讲解结束之后再附上完整代码，而本文KD树的实现和理解需要加上代码一起理解，所以在文中穿插了部分实现代码。完整代码参见我的Github：Github-zhangwenniu-KNN。

K近邻算法

        在最初接触K近邻算法之前，可能会将其与另一种无监督机器学习算法——K均值聚类算法混淆，K均值聚类算法是多个初始样本点在没有预标记样本类别的情况下，根据样本间距离的最近相邻策略，无监督的学习并将所有样本分类收敛至K个不同类别。
        与之进行区别的，K近邻算法是在预标记样本类别后，预测样本被输入进已标记的样本空间，根据其最近的K个不同的样本点的类别，投票产生待预测样本的类别。K近邻算法在使用过程中不构建模型，只是简单的依据不同样本多个特征条件下的距离关系，查询样本中的最近距离。对于样本空间上具有显著距离区域区分的多类别而言，K近邻算法的分类效果很好。这是一种惰性的学习策略，他没有显式的学习过程，在查询某个样本之前，并不预处理数据，直到开始学习才会构建分类模型。
        援引《数据挖掘十大算法》一书中对K近邻算法的描述：

KNN分类方法很容易理解和实现，并且它在许多情况下都表现非常良好。根据Cover和Hart的研究显示¹，在一定的情况下，最近邻规则的分类错误比率最多不会超过最优贝叶斯错误率的两倍，更进一步，一般情况下kNN方法的错误率都会渐进收敛到贝叶斯错误率，所以可以将kNN方法用于做贝叶斯的近似。

        K近邻分类算法可以在一定程度上替代贝叶斯算法，这一点我可能会在后续的贝叶斯分类算法分析的过程中体现。K近邻算法的思想很容易理解：给定N个被标记的样本数据、给定K作为K个用于选取最近K个相邻的样本个数、给定度量两样本之间距离的度量方法、给定类别选择的投票规则、给定待预测分类的样本，在N个样本中找到与待查询样本最近相邻的K个样本点，通过投票选择的方法，生成目标类别即可。下面给出K近邻算法的形式化语言描述。
        输入：训练样本集：$X=\{X_1,X_2,...,X_N\},Y=\{Y_1,Y_2,...,Y_N\},k$。
        其中$X_i=(X_i^{(1)},X_i^{(2)},...,X_i^{(n)})\in {\mathbb{R}}^n,Y_i\in \mathbb{R}=\{c_1,c_2,...,c_n\},X$为样本点，$Y$为分类的标签，$k$是用于度量最近特征的范围量，$n$是所有样本不同类别的集合。
        输出：实例$x$所属的类别$y$。同样也可以附带输出距离最近的k个点。
        1. 根据距离度量方法，找到实例$x$的$k$个最近相邻的样本点，记为$N_k(x)$。
        2. 使用投票表决规则，选择k个最近相邻样本点中出现次数最多的样本作为预测样本的类别$y$。即
$$y=arg\underset{c_j}{\max }\sum _{x_i\in N_k(x)}I(y_i=c_j),i=1,2,...,N;j=1,2,...,n.\text{\hspace{1em}(1)}$$

        这种方式理解起来最为直观，以K=1进行最近邻分类为例，只需要每次查询的时候逐个比较N个数据与待查询实例向量之间的关系，记录一个最近的节点即可。样本量为一万的时候，每个查询需要比较一万次用于分类，下面介绍一种K近邻算法的二叉查找树KD树方式，可以将每次最近邻查找的比较次数降低到$O({\log }_n)$，即一万个样本量查询次数约为14次，大大降低了运算的时间复杂度。

KD树

        KD树(K-Dimension Tree)是一种对于多维数据进行二叉查找的树形结构。不同于前文中K近邻算法中的K表示最近相邻的K个实例向量，KD树中的K表示数据的维度是K，例如下图中的KD树是3-Dimension-Tree，三维数据查找树；另一个则是2-Dimension-Tree二维数据查找树。关于绘制平衡查找树的图像以及如何对齐，我另外写了一篇博客，参见Python数据分析(02) graphviz绘制KD二叉查找树。

三维数据查找树

二维数据查找树

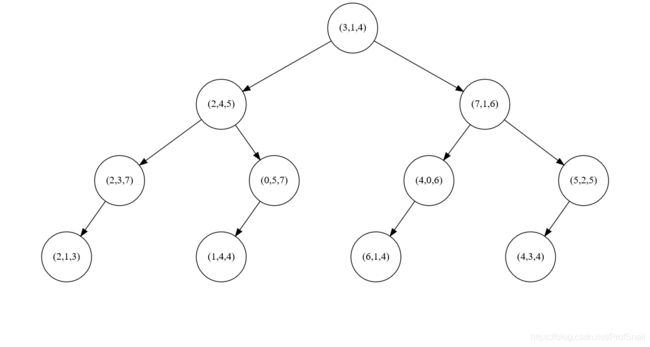
生成KD树

        KD树有多种实现方式，一些方式使用方差最大的维度作为每一层查找时候的数据维度，以保证分类的维度上样本数据分布最为分散。本文与李航《统计学习方法》中介绍的方法保持一致。生成KD树的方法给出如下递归化表述：
        1. 维度从$\{1,2,3,...,k\}$逐个选取，记当前选择的维度为$k_i$，并将样本组在该维度$k_i$下的中位数所在样本作为目前根节点，记为$root$。
        2. 将所有第$k_i$维中位数左侧的数据分为一组，用于生成$root$的左子树，左子树选择的维度为$(k_i+1)\mathrm{m}\mathrm{o}\mathrm{d}k$。
        3. 将所有第$k_i$维中位数右侧的数据分为一组，用于生成$root$的右子树，右子树选择的维度为$(k_i+1)\mathrm{m}\mathrm{o}\mathrm{d}k$。
        4. 当样本组为空的时候，当前节点记为空节点，返回上一层。
        经过这4个步骤，就可以建立一棵完整的KD树。观察上图中的三维查找树，根节点左侧的所有节点都小于等于(3,1,4)的第一维数据3，右侧的所有节点都大于等于(3,1,4)的第一维数据3;同理，第二层节点的左子树的第二维数据都小于等于该节点的第二维数据，右子树的第二维数据都大于等于该节点的第二维数据。C++实现代码如下：

// KD树中的节点
struct node {
	int index;
	int depth;
	node* left, *right, *father;
	node() {
		index = depth = -1;
		left = right = father = NULL;
	}
};
// 生成KD树
node* createKDTree(vector<int>& index, int depth) {
	if (index.empty()) {
		return NULL;
	}
	node* root = new node();
	root->depth = depth;
	int dim = depth % n;
	vector<pair<double, int> > vt;
	// 根据数值和索引生成数组，用于选择标准的中位数。
	for (auto id : index) {
		vt.push_back(pair<double, int>(data[id][dim], id));
	}
	sort(vt.begin(), vt.end());
	int num = vt.size();
	// 无论奇偶，设置中位数的节点为第n/2个。
	root->index = vt[num / 2].second;
	vector<int> left;
	for (int i = 0; i < num / 2; i++) {
		left.push_back(vt[i].second);
	}
	vector<int> right;
	for (int i = num / 2 +1; i < num; i++) {
		right.push_back(vt[i].second);
	}
	// 递归生成左右KD树。
	root->left = createKDTree(left, depth + 1);
	root->right = createKDTree(right, depth + 1);

	// 为了回溯寻找最近点，需要保存父节点。
	if (root->left)root->left->father = root;
	if (root->right)root->right->father = root;
	return root;
}

        树形结构一般需要另外的插入和删除操作。但是无论插入或者删除操作，都需要重新计算各个维度上的中位数，很可能导致原有结构被直接破坏，需要重新构建一棵完整的KD树。除了重新构建完整KD树之外，也有采取替罪羊树方法维护KD树的插入和删除操作，具体方法是插入操作、删除操作的节点虽然破坏了树的结构，但是暂时不重新建树，而是设置一个重建阈值，当树的待删除节点数量超过了阈值比例，则重建该子树。由于插入和删除操作过于繁琐，并且在训练之前一般已经标记好了数组内容，构建KD树已经足够满足训练所需。关于KD树的更详细介绍参见KD树算法分析。
        以上文中的二维二叉树的图形为例，我们在二维平面上感受一下这张KD树的图形。

2-Dimension-Tree的二维平面展示

        可以看到，这六个点将平面分为了七个不同的子区域，这是由二叉树的性质决定的。n个数据形成n个非叶子节点，出度为2n，除了根节点之外的n-1个节点占据n-1个出度，剩余出度数量为2n-(n-1)=n+1。这意味着任何一个数据在查询过程中，一定可以根据区分的维度，最后找到一个包含该数据的最小子区域，且该子区域包含于n+1的区域之中，是KD树中叶子结点的一个左右空节点之一。

通过KD树查询最近邻节点

        KD树的本质是按照不同的维度，根据数据的中位数划分出垂直于该维度的超平面，将数据分为左右两侧。算法描述如下：

1. 首先初始选择一个节点作为最近相邻节点。 这个节点是根据KD树查询数据$x$找到的叶节点，对于每一层节点node而言，其数据记为node.data，并且该节点作为分类超平面时，是维度node.dim下的中位数。如果$x_{[dim]}\le node.dat{a}_{[dim]}$则向当前节点的左子树继续查询；否则像当前节点的右子树继续查询，直到查询到叶子节点为止。该节点是包含$x$的最小子区域。
2. 在第一步的过程中，记录从根节点到叶子结点的路径，放入路径栈中。
3. 记第一步查询到的叶子节点为$leaf$，暂定$leaf$为距离$x$最近的节点，后续再更新该距离。$minDis$赋值为$leaf$与待分类数据$x$之间的距离，$nearestNode$赋值为$leaf$。注意，该节点只是一个初始化的方法，实际上任何一个节点都可能比该叶子节点距离$x$更近，这里只是将最近距离初始到包含$x$的最小区域节点处。
4. 当路径栈不为空的时候，取出栈顶元素，记为$top$。由于路径上的每个元素都有可能距离$x$更近，比较$top$和$x$的距离是否比之前的$minDis$更近，如果更近则更新最近距离和最近节点。
5. 继续判断以$x$为中心，以$minDis$构成的多维球体是否与$top$的两个子区域相交，如果相交，则更近的节点可能出现在该区域中，当该区域未曾访问过时，就将相交区域的节点送入路径栈中。注意，由于我们初始化位置是叶子节点，并且递归返回根节点，要判断是否刚刚从某个子区域搜寻回到父节点，父节点又发现这个回来的子区域和x的超圆相交，防止重复访问同一个子区域。
6. 重复4,5两个步骤，直到堆栈为空。因为不会重复访问同一棵子树，所以在有限样本的情况下一定会在有限步骤内终止。

        初学者会在判断超圆与超平面相交的地方犯迷糊：什么是超圆？什么是圆和平面相交？为什么不相交就一定不会出现在该子区域？为什么相交了还只是有可能出现，而不是一定出现？如何判定超圆与平面相交？这其实就是我在学习过程中出现的问题，下面我们通过一个实例演示来理解这个过程。假设当前空间仍然是上文中提到的二维KD树下的数据X=[(2,3), (4,7), (5,4), (7,2), (8,1), (9,6)]，待查找数据为(4,3)。

1. 根据(4,3)查询叶节点。找到包含(4,3)的区域为(2,3)的右半区，记(2,3)为当前暂定的最近相邻节点，超圆情况如下。可以看到，当前以x为圆心，以最近距离为半径画的圆内包括了另一个点(5,4)，而(5,4)才是真正的最近相邻点。另外的区域(8,1),(9,6)已经在当前最短半径的圆形以外，不可能距离更近，所以不用搜寻(7,2)的右半侧点。
   

2. 初始搜寻叶节点过程中的路径放入堆栈中，目前的堆栈内点为[(7,2), (5,4), (2,3)]。弹出(2,3)后，由于(2,3)的左右两侧不再具有子节点，不用继续搜索(2,3)的左右节点。

3. 栈内点为[(7,2), (5,4)]继续弹出(5,4)节点，比较发现(5,4)距离待查询点(4,3)距离更近，所以将最近点更新至(5,4)。(5,4)作为分类点时维度为第二维，发现该圆形与(5,4)的上面区域相交，最近点可能在上半区域，于是将上侧节点(4,7)压入栈中。
   

4. 栈内节点为[(7,2), (4,7)]，弹出栈顶元素(4,7)，比较发现该点距离待查询节点距离不会更短，因此不更新最近节点。且(4,7)已经是叶子节点，不再继续查找其子区域。
   

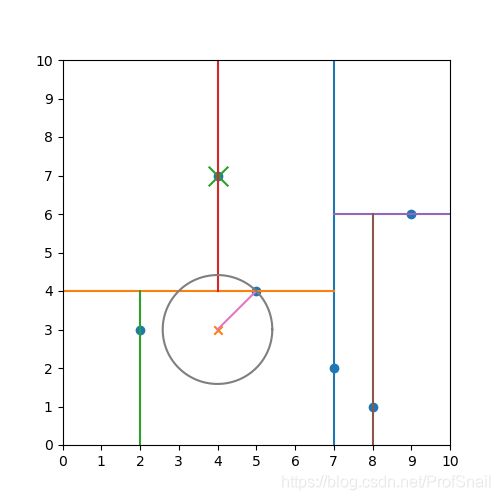
5. 栈中元素为[(7,2)]，弹出栈顶元素(7,2)。发现该节点不比当前最近节点更近，不更新最近节点。且发现超圆与超平面不相交，因此也不查询另一半子区域。至此，查询结束，最近点为(5,4)，最近距离为$\sqrt{2}$。
   
           至此，最近相邻算法已经表述完毕，只有当超圆与分类超平面相交时，才需要查询其另一半子区域，查询的平均时间复杂度为$O(logn)$。下面给出C++代码实现。

int NearestSearch(vector<double> x) {
	// 根据某个节点，寻找最近相邻点。
	if (x.size() != n) {
		printf("Input data error. Dimension not match.\n");
		exit(5);
	}
	// 根据维度与中位数的大小关系，选择最底层叶节点为初始最近节点。
	stack<node*> st;
	// 在寻找叶节点的过程中，添加进来路径。
	node* nearest = findLeaf(x, head, st);
	Distance d = Distance(2);

	// 以叶节点作为当前最近节点。
	double minD = d.Minkowski(x, data[nearest->index]);
	node* minNode = nearest;

	// 使用布尔数组进行打表，防止重复访问同一个节点分支。
	vector<bool> vis(data.size(), 0);
	while (!st.empty()) {
		// 回溯路径。
		node* top = st.top();
		vis[top->index] = 1;

		// 输出当前访问节点。
		/*
		cout << top->index << " " << top->depth << " Data: ";
		for (auto dt : data[top->index])cout << dt << " ";
		cout << endl;
		*/

		st.pop();

		// 计算当前节点是否更优，如果距离目标节点更近，则更新最近节点索引以及最近距离。
		double tempD = d.Minkowski(x, data[top->index]);
		if (tempD < minD) {
			minD = tempD;
			minNode = top;
		}

		// 输出更新之后的最近距离。
		/*
		cout << minD << endl;
		*/

		// 比较当前节点所在的维度下，由目标节点与最短半径构成的超圆能否与其子节点相交。
		int dim = top->depth % n;

		// 能够与左子树相交，就说明目标节点在该维度下向左偏移后的最大值（偏移长度为半径），小于当前节点在当前分割维度的数值。
		// 能够与右子树相交，就说明目标节点在该维度下向右偏移后的最大值（偏移长度为半径），大于当前节点在当前分割维度的数值。
		int left = x[dim] - minD, right = x[dim] + minD;

		// 同时保证节点不为空、未访问过，才将节点放入路径栈中进行检索。
		if (left <= data[top->index][dim] && top->left && !vis[top->left->index]) {
			st.push(top->left);
		}
		if (right >= data[top->index][dim] && top->right && !vis[top->right->index]) {
			st.push(top->right);
		}
	}
	// 输出最短距离以及其对应的节点。
	printf("minD = %lf. \n", minD);
	printf("minNode index is %d, depth is %d, data is: ", minNode->index, minNode->depth);
	for (int i = 0; i < n; i++) {
		printf("%0.lf ", data[minNode->index][i]);
	}
	printf("\n");
	// 返回最近节点对应的下标。
	return minNode->index;
}

通过KD树查询K近邻节点

        经过上面的演示，可以得到查询KD树中K个最近相邻节点的步骤。在这里，我们需要维护一个大根堆，堆内元素维持为最近相邻的K个元素，堆顶元素是K个最近相邻的元素中距离最远的一个点，任何一个更近的节点，一定比第K远的距离更近，所以每次更新时候只需要比较与堆顶元素之间的距离即可，如果更近则将堆顶弹出，将新节点放入堆中。算法描述如下，我直接复用了上面最近相邻节点算法的描述过程，并增减了部分内容以贴合最近K相邻算法：

1. 首先初始化一个大根堆，将一个无穷大的距离的空节点放入堆中，这样任何一个点都会比当前无穷大距离更近，方便维护。在C++中，大根堆用优先队列加以维护。
2. 初始选择一个节点作为最近相邻节点。 这个节点是根据KD树查询数据$x$找到的叶节点，对于每一层节点node而言，其数据记为node.data，并且该节点作为分类超平面时，是维度node.dim下的中位数。如果$x_{[dim]}\le node.dat{a}_{[dim]}$则向当前节点的左子树继续查询；否则像当前节点的右子树继续查询，直到查询到叶子节点为止。该节点是包含$x$的最小子区域。
3. 在第一步的过程中，记录从根节点到叶子结点的路径，放入路径栈中。
4. $minKDis$赋值为无穷大，表示距离$x$最近K个节点中距离最大的点。注意，该节点只是一个初始化的方法，实际上任何一个节点都可能比$minKDis$距离$x$更近，这里只是将最近距离初始到包含$x$的最大无穷区域处。
5. 当路径栈不为空的时候，取出栈顶元素，记为$top$。如果堆中的数量小于K个，则将这个节点认为是距离$x$最近的K个节点之一，将其放入堆中。如果堆中数量已经满足K个，由于路径上的每个元素都有可能距离$x$更近，比较$top$和$x$的距离是否比之前的$minKDis$更近，如果更近则更新最近距离和最近节点。
6. 继续判断以$x$为中心，以$minKDis$构成的多维球体是否与$top$的两个子区域相交，如果相交，则更近的节点可能出现在该区域中，当该区域未曾访问过时，就将相交区域的节点送入路径栈中。注意，由于我们初始化位置是叶子节点，并且递归返回根节点，要判断是否刚刚从某个子区域搜寻回到父节点，父节点又发现这个回来的子区域和x的超圆相交，防止重复访问同一个子区域。
7. 重复5,6两个步骤，直到堆栈为空。因为不会重复访问同一棵子树，所以在有限样本的情况下一定会在有限步骤内终止。

        不难发现，只有在维护大根堆方面和K个最近相邻节点的关系上，算法与此前最近相邻算法存在差异，其余地方大体类似，大家可以将查询(4,3)节点的3个最近相邻节点的过程手动模拟，以体会算法的流程和含义。找到K个相邻节点之后，只需要进行投票即可。有文献采用的方法是距离更近的节点所投票的比例应该更高，只需要简单的在投票环节增加一个比重即可。为便于读者理解，这里每个近邻节点投票的权重相同，且都为1。下面给出K近邻算法的C++实现。

// 进行K近邻搜索的过程中，保存在优先队列中的节点。
struct knode {
	// KD树中的节点索引。
	int index;
	// 当前节点与目标检索数据的距离。
	double distance;
	// 用优先队列保证大根堆的堆顶元素是距离最大值。
	// 当队列内元素数量小于K的时候，向堆中添加元素。
	// 当队列元素大于K的时候，比较当前节点的距离是否比K个最小距离还要小，如果是的话则将其取代为顶点的位置。
	knode() {}
	knode(int _id, double _d) :index(_id), distance(_d) {}
	bool operator < (const knode& nd) const {
		return distance < nd.distance;
	}
};
vector<int> knSearch(vector<double> x, int k) {
	// 根据某个节点，寻找最近相邻点。
	if (x.size() != n) {
		printf("Input data error. Dimension not match.\n");
		exit(5);
	}
	if (k > data.size()) {
		printf("You're searching %d nearest data, while there is only %d data. \n", k, n);
		printf("Adjusted k to %d. \n", n);
		k = n;
	}
	// 根据维度与中位数的大小关系，选择最底层叶节点为初始最近节点。
	stack<node*> st;
	// 在寻找叶节点的过程中，添加进来路径。
	node* nearest = findLeaf(x, head, st);
	Distance d = Distance(2);

	// 以叶节点作为当前最近节点，逐层向上寻找K个最近相邻的节点。
	// 设置一个最大距离为无穷大，则K个最近相邻的节点一定在距离查找节点的无穷大球范围内。
	double maxMinKD = 1e8;

	// 使用布尔数组进行打表，防止重复访问同一个节点分支。
	vector<bool> vis(data.size(), 0);

	// 设置一个与待查询节点之间距离的大根堆，保证K个节点都要小于等于大根堆的堆顶距离。
	priority_queue<knode> q;
	q.emplace(knode(-1, maxMinKD));

	while (!st.empty()) {
		// 回溯路径。
		node* top = st.top();
		vis[top->index] = 1;

		// 输出当前访问节点。
		/*
		cout << top->index << " " << top->depth << " Data: ";
		for (auto dt : data[top->index])cout << dt << " ";
		cout << endl;
		*/
		st.pop();

		// 计算当前节点是否更优，如果是距离目标节点最近的K个范围之内，则更新索引队列。
		double tempD = d.Minkowski(x, data[top->index]);
		if (q.size() < k) {
			q.emplace(knode(top->index, tempD));
		}
		else {
			if (tempD <= q.top().distance) {
				q.pop();
				q.emplace(knode(top->index, tempD));
			}
		}
		maxMinKD = q.top().distance;

		// 输出更新之后的K最近距离。
		/*
		cout << maxMinKD << endl;
		*/
		// 比较当前节点所在的维度下，由目标节点与最短半径构成的超圆能否与其子节点相交。
		int dim = top->depth % n;

		// 能够与左子树相交，就说明目标节点在该维度下向左偏移后的最大值（偏移长度为半径），小于当前节点在当前分割维度的数值。
		// 能够与右子树相交，就说明目标节点在该维度下向右偏移后的最大值（偏移长度为半径），大于当前节点在当前分割维度的数值。
		int left = x[dim] - maxMinKD, right = x[dim] + maxMinKD;

		// 同时保证节点不为空、未访问过，才将节点放入路径栈中进行检索。
		if (left <= data[top->index][dim] && top->left && !vis[top->left->index]) {
			st.push(top->left);
		}
		if (right >= data[top->index][dim] && top->right && !vis[top->right->index]) {
			st.push(top->right);
		}
	}
	// 输出最短距离以及其对应的节点。
	vector<int> ans;
	printf("maxMinKD = %lf. \n", maxMinKD);
	while (!q.empty()) {
		int idx = q.top().index;
		double dis = q.top().distance;
		ans.push_back(idx);
		q.pop();
		printf("Each node index is %d, distance is %lf. data is: ", idx, dis);
		for (int i = 0; i < n; i++) {
			printf("%0.lf ", data[idx][i]);
		}
		printf("\n");
	}
	// 返回K个最近节点对应的下标数组。
	return ans;
}

int vote(vector<double> x, int k) {
	// 获取K近邻节点的下标。
	vector<int> kNearest = knSearch(x, k);
	// 投票获取根据K近邻节点得到的类别值。
	unordered_map<int, int> mp;
	for (int& id : kNearest) {
		mp[label[id]]++;
	}
	int maxCount = 0, maxLabel = -1;
	// 投票
	for (auto it : mp) {
		if (it.second > maxCount) {
			maxCount = it.second;
			maxLabel = it.first;
		}
	}
	// 输出数据及其被投票得到的结果。
	printf("Data: ");
	for (int i = 0; i < x.size(); i++) {
		printf("%.0lf ", x[i]);
	}
	printf("is labeled as %d, poll num is  %d.", maxLabel, maxCount);
	return maxLabel;
}

至此，K近邻算法已经基本实现完成。

K近邻算法三大要素

        K近邻算法有三大要素：距离标准、K值确定、投票方法。距离度量标准有明可夫斯基距离（Minkowski Distance)，对于n维向量$x_1,x_2$而言，距离表示为：
$$MinkowskiDistance(x_1,x_2,p)=(\sum _{i=1}^n|x_1^{(i)}-x_2^{(i)}{|}^p{)}^{{}^{\frac{1}{p}}}\text{\hspace{1em}(2)}$$
        当$p=1$时，明可夫斯基距离退化为曼哈顿距离(Manhattan Distance)。
$$L_1(x_1,x_2)=(\sum _{i=1}^n|x_1^{(i)}-x_2^{(i)}|)\text{\hspace{1em}(3)}$$
        当$p=2$时，明可夫斯基距离化为欧氏距离(Euclidean Distance)。
$$L_2(x_1,x_2)=(\sum _{i=1}^n|x_1^{(i)}-x_2^{(i)}{|}^2{)}^{{}^{{}^{\frac{1}{2}}}}\text{\hspace{1em}(4)}$$
        当$p=+\infty$时，明可夫斯基距离化为两个向量所有维度中坐标距离的最大值。
$$L_{\infty }(x_1,x_2)=\underset{i=1}{\overset{n}{\max }}|x_1^{(i)}-x_2^{(i)}|\text{\hspace{1em}(5)}$$
        设计一个距离类以计算两点之间的距离。

class Distance {
public:
	int k;
	Distance(int _k):k(_k) {}
	double Minkowski(vector<double> x, vector<double> y) {
		int n = x.size();
		if (x.size() != y.size()) {
			printf("Error Message: in Distance.Minkowski(). \n");
			printf("x.size() = %d, y.size() = %d. They are guaranteed to be same. ", x.size(), y.size());
			exit(-1);
		}
		double dis = 0;
		if (k == INF) {
			// k趋于无穷的时候，就应该是所有坐标距离的最大值。
			for (int i = 0; i < n; i++) {
				dis = max(dis, abs(x[i] - y[i]));
			}
		}
		else {
			for (int i = 0; i < n; i++) {
				dis += pow(fabs(x[i] - y[i]), k);
			}
			dis = powf(dis, 1.0 / k);
		}
		return dis;
	}
};

        至于k值的确定，一般在工程中采用多折交叉验证的方式，将原始数据分为训练集、验证集、测试集。根据比对选择最适合的k数值。一定情况下，最近邻算法甚至优于K近邻算法。
        投票方法，也就是分类决策规则，在上文中已经提到过，不再赘述。
        至此，已经将K近邻算法讲述完毕。上文中的代码块被封装在类KNN中，完整代码已经更新在我的GitHub仓库：Zhangwenniu-Statistic-Learning-Method中，经过测试可以完整使用，只需要编译knn.cpp文件，将需要的数据按要求放入data.txt文本中即可实现KNN算法的模拟，并支持绘制KD二叉树，同时我也会继续更新《机器学习方法》的C++实现，并维护在我的GitHub仓库中。欢迎大家共同学习。
        一篇文章又写了一个礼拜，深感写作的不易啊。继续向李航老师致敬。欢迎大家留言讨论，一键三连那！

本文参考文献：
李航《统计学习方法》
Xindong Wu, Vipin Kumar《数据挖掘十大算法》

---

1. T. Cover and P. Hart, Nearest neighbor pattern classification. IEEE Transactions on Information Theory, 13(1): 21-27, January 1967. ↩︎