leetcode刷题--链表

题目分类 题目编号

链表的删除 203、237、19

链表的遍历 430

链表的旋转与反转 61、24、206、92、25

链表高精度加法 2、445

链表的合并 21、23

1. 203 移除的元素

解法：

链表的删除其实就是将该节点从链表中删除，并且将该节点的前面一个节点与该节点后面一个节点相连。可以使用递归或者迭代的方式来解决。我使用的是迭代的方式

• 若头节点的值为val,则移动头节点，直至头节点的值不为val。注意此时头节点移动之后，应该将头节点的内存释放
• 之后则按照迭代方式，设cur为当前节点，如果cur的下一个节点不为空，并且下一个节点的节点值等于va l，则删除下一个节点。
• 删除操作为$cur->next=cur->next->next$ ，同时注意释放内存空间
• 如果tmp的下一个节点不为val,则移动cur到下一个节点。
• 当cur的next为null时，结束遍历。

代码：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) {
     //如果头节点等于val
     while(head!=NULL && head->val==val){
       ListNode *tmp=head;
       head=head->next;
       delete tmp;
     }
     ListNode*cur=head;
     while(cur!=NULL&&cur->next!=NULL){
       if(cur->next->val==val){
         ListNode* tmp=cur->next;
         cur->next=cur->next->next;
         delete tmp;
       }
       else
       cur=cur->next;
     }
     return head;
    }
};

另外，由于这里删除头节点使用了额外的逻辑，但是在头节点前创建一个虚拟头节点dummyHead，那么删除头节点和删除其他节点的逻辑相同，最后返回dummyHead.next就是删除操作后的头节点，具体可见官方题解

203. 移除链表元素 - 力扣（LeetCode）

时间复杂度：O(n) 其中n 是链表的长度。需要遍历链表一次。

空间复杂度：O(1)

2. 237 删除链表中的节点

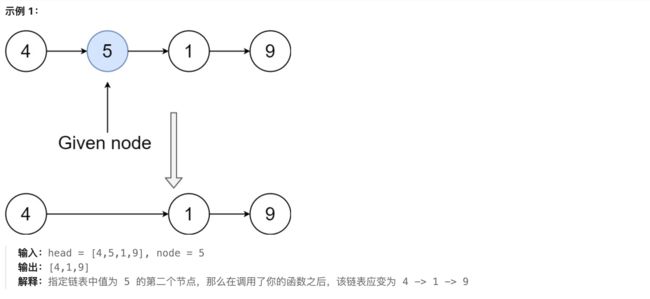
解法：正常的删除链表中的元素需要知道上一个节点的位置，但是题目中只给出了删除的节点，因此不能使用一般的做法。但是由于知道了下一个节点的值，

可以将下一个节点的值赋给要删除的节点。

例如[4，5，1，9]，删除的为1，可以将9赋给1，则变为[4,5,9,9]同时，只要将第一个9，即我们要删除的节点node，$node->next=node->next->next$

既可以跳过第二个9。注意c++ 中的内存释放，虽然不释放也不会报错

代码：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    void deleteNode(ListNode* node) {
       node->val=node->next->val;
       ListNode *tmp=node->next;
       node->next=tmp->next;
       delete tmp;
    }
};

时间复杂度：o(n)

空间复杂度：o(1)

3. 19 删除链表的倒数第N个节点

解法一：双指针（使用）

• 引入虚拟头节点dumpy，以及快慢指针【也常用的判断链表有环的场景】first,second，first领先second指针n个节点
• 那么当first指针的next为null的时候，second正好指在待删除节点的前驱节点，按照链表删除节点的逻辑进行删除即可

代码：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode * dummy=new ListNode(0,head);
        ListNode *first,*second;
        first=dummy;
        second=dummy;
        for(int i=0;inext;
        }
        while(first->next!=NULL){
            first=first->next;
            second=second->next;
        }
        ListNode * tmp=second->next;
        second->next=tmp->next;
        delete tmp;
        ListNode*ans=dummy->next;
        delete dummy;
        return ans;
    }
};

时间复杂度：o(n)

空间复制度：o(1)

解法二：计算链表长度

最容易的方法：从头节点开始对链表进行一次遍历，得到链表的长度L。然后就能得到要删除的节点的位置是L-n+1。

删除链表的其中的一个节点的话,最经常会添加一个虚拟头节点。这样会使得删除的节点不管是否为头节点的逻辑相同。

解法三：用栈

我们也可以在遍历链表的同时将所有节点依次入栈。根据栈「先进后出」的原则，我们弹出栈的第 nnn 个节点就是需要删除的节点，并且目前栈顶的节点就是待删除节点的前驱节点。

解法二和三见：19. 删除链表的倒数第 N 个结点 - 力扣（LeetCode）

4. 430 扁平化多级双向链表

解法一：看成二叉树的先序遍历，child为左节点，next为右节点，即：

遍历的过程中利用pre记录这个遍历节点的前驱节点，记得连接本节点和前驱节点之间的前向后向指针。

代码：

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* prev;
    Node* next;
    Node* child;
};
*/

class Solution {
public:
    Node*pre=NULL;
    //树的先序列遍历
    Node* flatten(Node* head){
        if(head==NULL)
            return NULL;
        Node*child=head->child;
        Node*next=head->next;
        if(pre){
            pre->next=head;
            head->prev=pre;
        }
        head->child=NULL;
        pre=head;
        flatten(child);
        flatten(next);
        return head;
    }
};

时间复杂度：O(n)

空间复杂度：O(n) 为栈空间

解法二：栈递归

当我们遍历到某个节点 node 时，如果它的 child 成员不为空，那么我们需要将child 指向的链表结构进行扁平化，并且插入 node 与 node 的下一个节点之间。

因此，我们在遇到 child 成员不为空的节点时，就要先去处理child 指向的链表结构，这就是一个深度优先搜索的过程。当我们完成了对 child 指向的链表结构的扁平化之后，就可以回溯node 节点。

因为扁平化的链表需要插入node和node的下一个节点中，因袭，需要知道扁平化的最后一个节点last

我们可以使用栈保存最后的节点，当我们遇到有孩子的节点，如果该节点的next不为空，则将next节点如栈，当遍历到next节点为空了，即看栈中有无节点，栈中的节点是原本node的next节点，和扁平化后的last相连。

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* prev;
    Node* next;
    Node* child;
};
*/

class Solution {
public:
    stacks;
    Node* flatten(Node* head){
        Node *cur=head;
        while(cur!=NULL){
            if(cur->child!=NULL){
                if(cur->next!=NULL)
                s.push(cur->next);
                 Node* child=cur->child;
                 cur->next=child;
                 child->prev=cur;
                 cur->child=NULL;
            }
            if(cur->next==NULL&&!s.empty()){
                Node*next=s.top();
                s.pop();
                cur->next=next;
                next->prev=cur;
            }
            cur=cur->next;
        }
        return head;
    }
};

时间复杂度：O(n)

空间复杂度：O(n) 为栈空间

5. 61 旋转链表

解法一：用双端队列迭代

• 首先解决特殊情况，若head为null或者head->next为null则可以直接返回head

• 注意到旋转1次就是将最末尾的节点移动到第一个，并修改相应的next指针，k为几则移动几次

• 因此，使用双端队列，队列的尾部为每次需要移动的节点，移动一次需要将队列末尾节点移动到队首，并且此时队列末尾的节点的next指针为null。新队首指针的next也需要指向原来的队首节点

• 循环k次返回队首为此时的head

  注意这种做法可能使得k很大的时候超时，当k>=链表长度n时，如上述例子，k=4,n=3,其实旋转四次的结果就等于在最原始的基础上旋转一次

  因此k%n为真正需要旋转的次数

代码：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* rotateRight(ListNode* head, int k) {
        vectorstack;
        ListNode*cur=head;
        ListNode*pre,*next;
        if(head==nullptr||head->next==nullptr)
        return head;
        int len=0;
        while(cur!=nullptr){
            stack.push_back(cur);
            cur=cur->next;
            len++;
        }
        int l=k%len;
        for(int i=0;inext=nullptr;
            if(!stack.empty())
            next=stack.front();
            cur->next=next;
            stack.insert(stack.begin(),cur);
        }
        return stack.front();
    }
};

时间复杂度：O（n）

空间复杂度：O（n）

解法二：闭合为环（官方解法）

记给定链表的长度为 n，注意到当向右移动的次数 k≥n 时，我们仅需要向右移动kmodn 次即可。因为每 n 次移动都会让链表变为原状。这样我们可以知道，新链表的最后一个节点为原链表的第(n−1)−(k mod n) 个节点（从 0 开始计数）。

这样，我们可以先将给定的链表连接成环，然后将指定位置断开。

具体代码中，我们首先计算出链表的长度 nnn，并找到该链表的末尾节点，将其与头节点相连。这样就得到了闭合为环的链表。然后我们找到新链表的最后一个节点（即原链表的第 (n−1)−(kmodn) 个节点），将当前闭合为环的链表断开，即可得到我们所需要的结果。

特别地，当链表长度不大于 1，或者 kkk 为 n 的倍数时，新链表将与原链表相同，我们无需进行任何处理。

代码：

class Solution {
public:
    ListNode* rotateRight(ListNode* head, int k) {
        if (k == 0 || head == nullptr || head->next == nullptr) {
            return head;
        }
        int n = 1;
        ListNode* iter = head;
        while (iter->next != nullptr) {
            iter = iter->next;
            n++;
        }
        int add = n - k % n;
        if (add == n) {
            return head;
        }
        iter->next = head;
        while (add--) {
            iter = iter->next;
        }
        ListNode* ret = iter->next;
        iter->next = nullptr;
        return ret;
    }
};

• 时间复杂度：O(n)，最坏情况下，我们需要遍历该链表两次。
• 空间复杂度：O(1), 需要常数的空间存储若干变量。

6. 24 两两交换链表中的节点

解法一：迭代

创建哑节点dummpy,dummpy->next-head.cur表示当前带大的节点，初始化的时候cur=dummpy，每次需要交换其后的两个节点。如果cur的候选没有节点或者只有一个节点，结束交换。否则更新其之后的指针关系。

代码：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        ListNode *dummpy=new ListNode();
        dummpy->next=head;    
        ListNode*cur=dummpy;
        ListNode*tmp1,*tmp2;
        while(cur->next!=nullptr&&cur->next->next!=nullptr){
            tmp1=cur->next;
            tmp2=cur->next->next;
            cur->next=tmp2;
            tmp1->next=tmp2->next;
            tmp2->next=tmp1;
            cur=tmp1;
        }
        return dummpy->next;
    }

};

• 时间复杂度：O(n)，其中 n 是链表的节点数量。需要对每个节点进行更新指针的操作。
• 空间复杂度：O(1)

解法二：递归

可以通过递归的方式实现两两交换链表中的节点。

递归的终止条件是链表中没有节点，或者链表中只有一个节点，此时无法进行交换。

如果链表中至少有两个节点，则在两两交换链表中的节点之后，原始链表的头节点变成新的链表的第二个节点，原始链表的第二个节点变成新的链表的头节点。链表中的其余节点的两两交换可以递归地实现。在对链表中的其余节点递归地两两交换之后，更新节点之间的指针关系，即可完成整个链表的两两交换。

用 head 表示原始链表的头节点，新的链表的第二个节点，用 newHead 表示新的链表的头节点，原始链表的第二个节点，则原始链表中的其余节点的头节点是 newHead.next。令 head.next = swapPairs(newHead.next)，表示将其余节点进行两两交换，交换后的新的头节点为 head 的下一个节点。然后令 newHead.next = head，即完成了所有节点的交换。最后返回新的链表的头节点 newHead。

见官方题解：24. 两两交换链表中的节点 - 力扣（LeetCode）

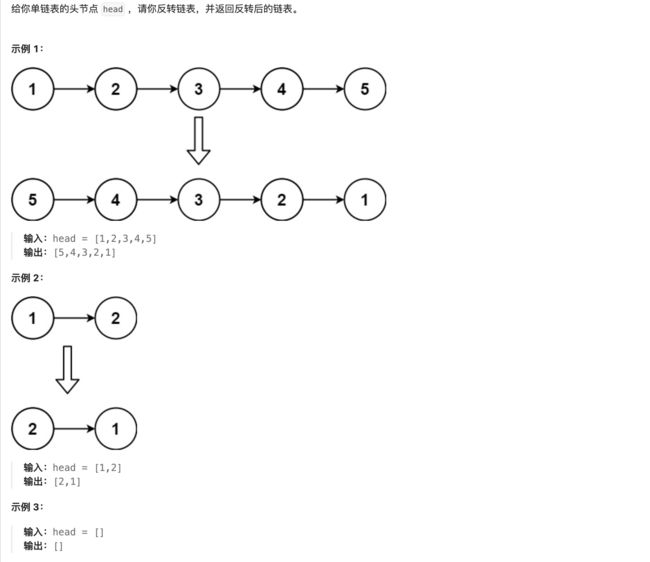
7. 206 反转链表

解法一：另外栈空间解决

根据栈的先进后出的特性，将节点顺序入栈，按照其出栈的顺序连接节点，即得到反转后的链表。栈顶节点为头节点，注意栈中最后一个节点需要指向null指针，否则成环。

代码：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        stacks;
        ListNode* newHead;
        if(head==nullptr||head->next==nullptr)
        return head;
        while(head!=nullptr){
            s.push(head);
            head=head->next;
        }
        newHead=s.top();
        s.pop();
        ListNode* cur=newHead;
        while(!s.empty()){
            cur->next=s.top();
            s.pop();
            cur=cur->next;
        }
        cur->next=nullptr;
        return newHead;
    }
};

时间复杂度：O(n)

空间复杂度：O(n)

解法二：迭代【在原来空间上操作，不需要额外的内存空间】

假设链表为 1→2→3→∅，我们想要把它改成 ∅←1←2←3。

在遍历链表时，将当前节点的next 指针改为指向前一个节点。由于节点没有引用其前一个节点，因此必须事先存储其前一个节点。在更改引用之前，还需要存储后一个节点。最后返回新的头引用。

代码：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode*pre=nullptr;
        ListNode*cur=head;
        while(cur!=nullptr){
            ListNode*tmp=cur->next;
            cur->next=pre;
            pre=cur;
            cur=tmp;
        }
        return pre;
    }
};

时间复杂度：O(n)

空间复杂度：O(1)

解法三：递归

见题解：206. 反转链表 - 力扣（LeetCode）

代码：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        return recur(head,nullptr);
    }
private:
ListNode*recur(ListNode*cur,ListNode*pre){
    if(cur==nullptr)
        return pre;
    ListNode*res=recur(cur->next,cur);
    cur->next=pre;
    return res;    
}   
};

时间复杂度 O(N ： 遍历链表使用线性大小时间。
空间复杂度 O(N) ： 遍历链表的递归深度达到 N ，系统使用 O(N) 大小额外空间。

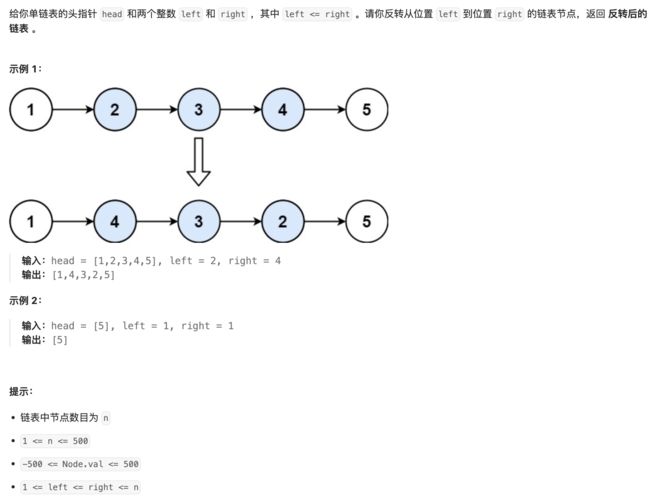
8. 92 反转链表II

解法一：

• 一次遍历找到反转区间的前一个节点pre和后一个节点next
• 利用栈将区间翻转：即弹栈并将pre与栈中节点相连

代码：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseBetween(ListNode* head, int left, int right) {
        int len=right-left+1;
        ListNode *dumpy=new ListNode();
        ListNode*cur=dumpy;
        dumpy->next=head;
        int cnt=0;
        ListNode*pre,*next;
        stacks;
        while(cntnext;
            cnt++;
        }
        pre=cur;
        cnt++;
        cur=cur->next;
        while(cnt<=right){
            s.push(cur);
            cur=cur->next;
            cnt++;
        }
        next=cur;
        while(!s.empty()){
            ListNode*tmp=s.top();
            s.pop();
            pre->next=tmp;
            pre=pre->next;
        }
        pre->next=next;
        return dumpy->next;
    }
};

时间复杂度：O(N)

空间复杂度：O(1)

解法二：**一次遍历。**将需要逆转的链表区间的左节点不动 ，将区间内的节点以此头插入左节点之后，实现反转链表，见官方题解

92. 反转链表 II - 力扣（LeetCode）

9. 25 K个一组翻转链表

解法：本题需要对局部区间链表进行翻转，主要抓住四个关键节点位置：

• reversePre：反转区间的前一个节点；
• reverseHead：反转区间的头节点；
• reverseTail：反转区间的尾节点；
• reverseNext：反转区间的下一个节点；

首先，引入dumpy节点，dumpy->next=head;

初始化:

• rPre=dumpy;
• rHead=dumpy->next;
• rTail=rPre;

然后移动rTail指针k次，移动的过程中判断是否rTail指针为空，若为空，则直接返回dumpy->next为翻转链表的头节点。

移动k次之后，我们翻转【rHead,rTail】之间的链表。

反转区间链表的过程：

• pre=rHead;

• cur=rHead->next;

• 注意cur的循环退出条件为当前rTail的next节点，因为反转过程中rTail的next节点会改变，可能造成问题。

  因此，while循环前，需要用rNext记录当前rTail的next节点。

• 翻转链表的过程如就是将cur指向pre的过程，然后移动pre和cur指针。

区间循环结束之后，此时的cur指针恰好为rNext位置，pre的位置是当前区间的头指针即rTail，

此时将rPre连接pre,rHead连接cur;

然后更新rTail和rPre指针的位置为rHead，rHead的位置为rNext

代码：

class solution75 {
public:
    ListNode* reverseKGroup(ListNode* head, int k) {
        ListNode *dumpy=new ListNode();
        dumpy->next=head;
        ListNode*rPre=dumpy;
        ListNode*rHead=dumpy->next;
        ListNode*rTail=dumpy;
        while(rTail!=nullptr){
            for(int i=0;inext;
                if(rTail==nullptr)
                {
                    return dumpy->next;
                }
            }
            //翻转rHead,rtail的链表
            ListNode*pre=rHead;
            ListNode*cur=rHead->next;
            ListNode*rNext=rTail->next;
            while(cur!=rNext){
                ListNode* tmp=cur->next;
                cur->next=pre;
                pre=cur;
                cur=tmp;
            }
            rPre->next=pre;
            rHead->next=cur;
            rTail=rHead;
            rPre=rHead;
            rHead=cur;
        }
        return dumpy->next;
    }
};

​

时间复杂度：O(n)，其中 n 为链表的长度。

空间复杂度：O(1，我们只需要建立常数个变量。

10. 21 合并两个有序链表

解法一：迭代

• 对于合并有序链表，可以和合并两个有序数组的相同处理方式，利用first的second指针分别指向list1和list2的头节点

• 同时设置哑节点dumpy，为了避免格外一些特殊情况判断

• 初始化时，cur=dumpy

• 那么则移动first和second指针，将其val值较小的节点连在cur之后，并且将这个指针后移动

  如果两个指针指向的val相同，则两个指针都需要向后移动，并且这两个节点都需要移到cur之后

• 当first或者second有一个为null结束循环，对于非空的指针，直接将cur->next与其相连

代码：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        ListNode * dump=new ListNode();
        ListNode*first=list1;
        ListNode*second=list2;
        ListNode*cur=dump;
        while(first!=nullptr&&second!=nullptr){
            if(first->valval){
                ListNode*tmp=first;
                first=first->next;
                cur->next=tmp;
                cur=cur->next;
            }
            else if(first->val>second->val){
                ListNode*tmp=second;
                second=second->next;
                cur->next=tmp;
                cur=cur->next;
            }
            else{
                ListNode*tmp1=first;
                first=first->next;
                ListNode*tmp2=second;
                second=second->next;
                cur->next=tmp1;
                cur=cur->next;
                cur->next=tmp2;
                cur=cur->next;
            }
        }
        if(first==nullptr&&second!=nullptr){
            cur->next=second;
        }
        else {
            cur->next=first;
        }
        return dump->next;
    }
};

时间复杂度：O(m+n)

空间复杂度：O(1)

解法二：递归 见官方题解21. 合并两个有序链表 - 力扣（LeetCode）

11. 23 合并k个升序链表

解法一：分治合并

由于合并k个有序数组，很容易想到的做法就是按照顺序，cur表示已经合并的链表，每次都将cur和下一个待合并链表进行合并。

解法二：使用优先队列合并

我们需要维护当前每个链表没有被合并的元素的最前面一个，k 个链表就最多有 k个满足这样条件的元素，每次在这些元素里面选取 val 属性最小的元素合并到答案中。在选取最小元素的时候，我们可以用优先队列来优化这个过程。

解法一二见官方题解：

23. 合并 K 个升序链表 - 力扣（LeetCode）

解法三：分治合并

• 采用分治的思想，首先将k个链表两两划分，直至划分到剩余两个单独的链表，然后利用合并两个有序链表的方式进行合并
• 类似归并排序的方式，先将k个链表切分成若干个子表，直到每个子表只包含一个元素
• 然后将子表合并，生成新的更长的链表
• 最后剩余的链表就是最终返回的有序链表

代码：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        ListNode * dump=new ListNode();
        ListNode*first=list1;
        ListNode*second=list2;
        ListNode*cur=dump;
        while(first!=nullptr&&second!=nullptr){
            if(first->valval){
                ListNode*tmp=first;
                first=first->next;
                cur->next=tmp;
                cur=cur->next;
            }
            else if(first->val>second->val){
                ListNode*tmp=second;
                second=second->next;
                cur->next=tmp;
                cur=cur->next;
            }
            else{
                ListNode*tmp1=first;
                first=first->next;
                ListNode*tmp2=second;
                second=second->next;
                cur->next=tmp1;
                cur=cur->next;
                cur->next=tmp2;
                cur=cur->next;
            }
        }
        if(first==nullptr&&second!=nullptr){
            cur->next=second;
        }
        else {
            cur->next=first;
        }
        return dump->next;
    }
    ListNode*merge(vector& lists,int l,int r){
        if(l==r)
        return lists[l];
        if(l>r)
        return nullptr;
        int mid=(l+r)/2;
        ListNode*left=merge(lists,l,mid);
        ListNode*right=merge(lists,mid+1,r);
        return mergeTwoLists(left,right);
    }
    ListNode* mergeKLists(vector& lists) {
       return merge(lists,0,lists.size()-1);
    }
};

时间复杂度：考虑递归「向上回升」的过程——第一轮合并 $\frac{k}{2}$ 组链表，每一组的时间代价是 O(2n)；第二轮合并$\frac{k}{4} $组链表，每一组的时间代价是 O(4n).所以总的时间代价是 $O({\sum }_{i=1}^{\infty }\frac{k}{2^i}\times 2^{i}n)=O(kn\times \log k)$故渐进时间复杂度为$O(kn\times \log k)$.
空间复杂度：递归会使用到 O(logk) 空间代价的栈空间。

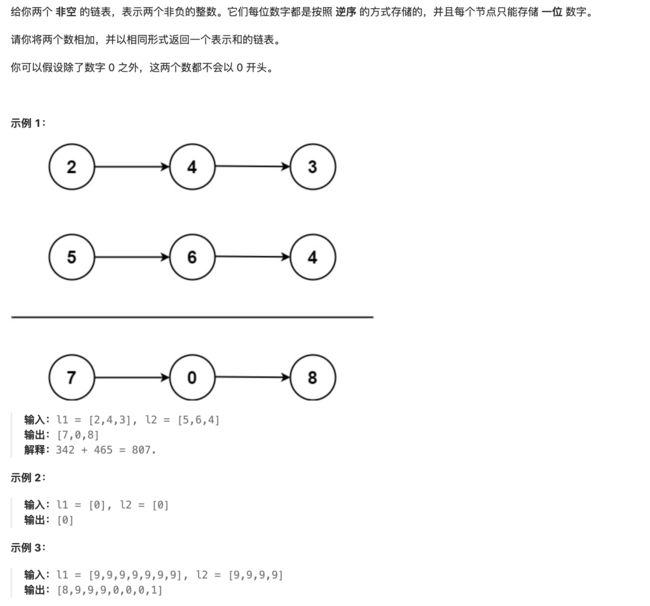
12. 2 两数相加

解法：

• 首先采用哑节点dumpy，dumpy的next即我们需要返回的头节点，之后由节点相加产生的新节点都连接在dumpy之后。

• 由于输入的两个链表都是逆序存储数字的位数的，因此两个链表中同一位置的数字可以直接相加。

• 我们同时遍历两个链表，逐位计算它们的和，并与当前位置的进位值相加。具体而言，如果当前两个链表处相应位置的数字为 n1,n2，进位值为 carry，则它们的和n1+n2+carry；其中，答案链表处相应位置的数字为 $(n1+n2+carry)mod10$，而新的进位值为$\lfloor \frac{n1+n2+\text{carry}}{10}\rfloor$

• 如果两个链表的长度不同，则可以认为长度短的链表的后面有若干个 0 。

注意容易错的位置：

如果链表遍历结束后，有carry>0，还需要在答案链表的后面附加一个节点，节点的值为 carry。

代码：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
     ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
         ListNode*dumpy=new ListNode();
         ListNode*cur;
         cur=dumpy;
         int carry=0;
         while(l1||l2){
             int n1=l1?l1->val:0;
             int n2=l2?l2->val:0;
             int sum=n1+n2+carry;
             carry=sum/10;
             sum=sum%10;
             ListNode*node=new ListNode(sum);
             cur->next=node;
             cur=cur->next;
             if(l1)
             l1=l1->next;
             if(l2)
             l2=l2->next;
         }
        if(carry>0){
            cur->next=new ListNode(carry);
        }
        return dumpy->next;  
    }
};

时间复杂度：O(max(m,n))其中m和n分别为两个链表的长度。

空间复杂度：O(1)

13. 445 两数相加II

解法一：三个栈翻转链表

• 由于2中两数相加为逆序，因此不需要翻转链表，只需要按位计算即可。这题中的两个链表是正序的。

• 首选将l1和l2中的节点入栈，result栈用于最后结果的反转

• 然后当这两个栈有一个栈不为空时，按照2中相似的方法计算，计算出的最终节点入result栈。

• 最后反转result栈，得到最终结果

代码：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
     ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        stackl1stack;
        stackl2stack;
        stackresult;
        ListNode*cur=l1;
        while(cur!=nullptr){
            l1stack.push(cur);
            cur=cur->next;
        }
        cur=l2;
        while(cur!=nullptr){
            l2stack.push(cur);
            cur=cur->next;
        }
        int flag=0;
        while(!l1stack.empty()&&!l2stack.empty()){
            int add1=l1stack.top()->val;
            l1stack.pop();
            int add2=l2stack.top()->val;
            l2stack.pop();
            int r;
            if(flag)
                r=add1+add2+1;
            else
                r=add1+add2;
            if(r>=10)
            {
                flag=1;
                r=r-10;
            }
            else{
                flag=0;
            }
            ListNode*node=new ListNode(r);
            result.push(node);
        }
        if(!l1stack.empty()&&l2stack.empty()){
            while(!l1stack.empty()){
                int add=l1stack.top()->val;
                if(flag)
                 add++;
                if(add>=10)
                {
                    add=add-10;
                    flag=1;
                }
                else {
                    flag = 0;
                }
                l1stack.pop();
                ListNode*node=new ListNode(add);
                result.push(node);
            }
            if(flag){
                ListNode*node=new ListNode(flag);
               result.push(node);
            }
        }
        else{
            while(!l2stack.empty()){
                int add=l2stack.top()->val;
                if(flag)
                    add++;
                if(add>=10)
                {
                    add=add-10;
                    flag=1;
                }
                else {
                    flag = 0;
                }
                l2stack.pop();
                ListNode*node=new ListNode(add);
                result.push(node);
            }
            if(flag){
                ListNode*node=new ListNode(flag);
               result.push(node);
            }
        }
       ListNode*dumpy=new ListNode();
       cur=dumpy;
        while(!result.empty()){
            cur->next=result.top();
            result.pop();
            cur=cur->next;
        }
        return dumpy->next;
    }
};