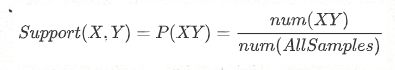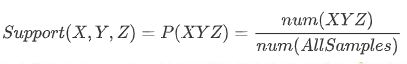关联规则之Apriori算法

目录

一、关联规则

二、Apriori算法

2.1 Apriori算法思想

2.2 Apriori算法流程

原文链接：https://www.cnblogs.com/pinard/p/6293298.html

---

一、关联规则

关联规则分析(Association Rule Analysis)是为了发掘数据背后的关联关系而诞生的。

我们可以定义一个关联规则：

其中，X，Y分别表示两个互斥事件，Y称为前因，X称为后果，上述的关联规则表示Y会导致X。但是我们又怎么评判这两个事件之间的关系强弱呢？我们能够通过频繁项集的评估标准来进一步分析。

在常用的频繁项集的评估标准中有支持度,置信度和提升度三个：

频繁项集：频繁模式是指数据集中频繁出现的项集、序列或子结构。频繁项集是指支持度大于等于最小支持度(min_sup)的集合。

---

支持度：几个关联的数据在数据集中出现的次数占总数据集的比重，或者说几个数据关联出现的概率。如果我们有两个想分析关联性的数据X和Y，则对应的支持度为:

以此类推，如果我们有三个想分析关联性的数据X，Y和Z，则对应的支持度为:

一般来说，支持度高的数据不一定构成频繁项集，但是支持度太低的数据肯定不构成频繁项集。

置信度：一个数据出现后，另一个数据出现的概率，或者说数据的条件概率。如果我们有两个想分析关联性的数据X和Y，X对Y的置信度为：

也可以以此类推到多个数据的关联置信度，比如对于三个数据X，Y，Z,则X对于Y和Z的置信度为：

提升度：表示含有Y的条件下，同时含有X的概率，与X总体发生的概率之比

提升度体现了X和Y之间的关联关系,，Lift(X⇐Y)可以表示Y的出现对X出现的概率提升的程度：

提升度 Lift(X⇐Y) ＞ 1 则 X⇐Y 是有效的强关联规则；

提升度 Lift(X⇐Y) ≤ 1 则 X⇐Y 是无效的强关联规则 ；

一个特殊的情况，如果X和Y独立，则有 Lift(X⇐Y) = 1，因为此时P(X|Y)=P(X)。

---

案例：

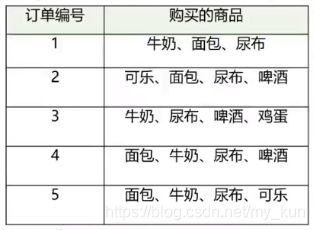
以下表中的商品为例计算并理解支持度、置信度和提升度。

“牛奶”的支持度：4/5=0.8 【“牛奶”共出现4次，总订单数为5】

“牛奶+面包”的支持度：3/5=0.6 【“牛奶+面包”共出现3次，总订单为5】

 

“啤酒 ⇐ 牛奶”的置信度：2/4=0.5 【“牛奶”出现4次，“啤酒”在“牛奶”出现的条件下出现了2次】

“牛奶 ⇐ 啤酒”的置信度：2/3=0.67 【“啤酒”出现了3次，“牛奶”在“啤酒”出现的条件下出现了2次】

 

“啤酒 ⇐ 牛奶”的提升度：0.5/0.6=0.83 【“啤酒 ⇐ 牛奶”的置信度为0.5，“啤酒”的支持度为0.6】

通过最后的“啤酒 ⇐ 牛奶”的提升度我们可以说牛奶的出现并不能很好的提高啤酒的出现，也就是牛奶并不能促进啤酒的销售。

二、Apriori算法

2.1 Apriori算法思想

       对于Apriori算法，我们使用支持度来作为我们判断频繁项集的标准。Apriori算法的目标是找到最大的K项频繁集。这里有两层意思，首先，我们要找到符合支持度标准的频繁集。但是这样的频繁集可能有很多。第二层意思就是我们要找到最大个数的频繁集。比如我们找到符合支持度的频繁集AB和ABE，那么我们会抛弃AB，只保留ABE，因为AB是2项频繁集，而ABE是3项频繁集。那么具体的，Apriori算法是如何做到挖掘K项频繁集的呢？

　　Apriori算法采用了迭代的方法，先搜索出候选1项集及对应的支持度，剪枝去掉低于支持度的1项集，得到频繁1项集。然后对剩下的频繁1项集进行连接，得到候选的频繁2项集，筛选去掉低于支持度的候选频繁2项集，得到真正的频繁二项集，以此类推，迭代下去，直到无法找到频繁k+1项集为止，对应的频繁k项集的集合即为算法的输出结果。

　　可见这个算法还是很简洁的，第i次的迭代过程包括扫描计算候选频繁i项集的支持度，剪枝得到真正频繁i项集和连接生成候选频繁i+1项集三步。

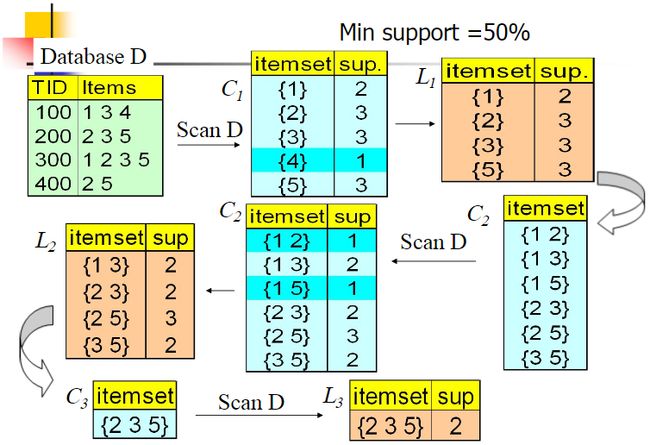
　　我们下面这个简单的例子看看：

　　我们的数据集D有4条记录，分别是134,235,1235和25。现在我们用Apriori算法来寻找频繁k项集，最小支持度设置为50%。首先我们生成候选频繁1项集，包括我们所有的5个数据并计算5个数据的支持度，计算完毕后我们进行剪枝，数据4由于支持度只有25%被剪掉。我们最终的频繁1项集为1235，现在我们链接生成候选频繁2项集，包括12,13,15,23,25,35共6组。此时我们的第一轮迭代结束。

　　进入第二轮迭代，我们扫描数据集计算候选频繁2项集的支持度，接着进行剪枝，由于12和15的支持度只有25%而被筛除，得到真正的频繁2项集，包括13,23,25,35。现在我们链接生成候选频繁3项集,123, 135和235共3组，这部分图中没有画出。通过计算候选频繁3项集的支持度，我们发现123和135的支持度均为25%，因此接着被剪枝，最终得到的真正频繁3项集为235一组。由于此时我们无法再进行数据连接，进而得到候选频繁4项集，最终的结果即为频繁3三项集235。

2.2 Apriori算法流程

输入：数据集合D，支持度阈值α（支持度阈值一般为经验值或实验值）

输出：最大的频繁k项集

　　1）扫描整个数据集，得到所有出现过的数据，作为候选频繁1项集。k=1，频繁0项集为空集。

　　2）挖掘频繁k项集

　　　　a) 扫描数据计算候选频繁k项集的支持度

　　　　b) 去除候选频繁k项集中支持度低于阈值的数据集,得到频繁k项集。如果得到的频繁k项集为空，则直接返回频繁k-1项集的集合作为算法结果，算法结束。如果得到的频繁k项集只有一项，则直接返回频繁k项集的集合作为算法结果，算法结束。

　　　　c) 基于频繁k项集，连接生成候选频繁k+1项集。

　　3） 令k=k+1，转入步骤2。

　　　　从算法的步骤可以看出，Aprior算法每轮迭代都要扫描数据集，因此在数据集很大，数据种类很多的时候，算法效率很低。