LeetCode刷题
一 【移除元素】
原题链接:27. 移除元素 - 力扣(LeetCode)
给你一个数组
nums和一个值val,你需要 原地 移除所有数值等于val的元素,并返回移除后数组的新长度。不要使用额外的数组空间,你必须仅使用
O(1)额外空间并 原地 修改输入数组。元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
示例 1:
输入:nums = [3,2,2,3], val = 3 输出:2, nums = [2,2] 解释:函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如,函数返回的新长度为 2 ,而 nums = [2,2,3,3] 或 nums = [2,2,0,0],也会被视作正确答案。
示例 2:
输入:nums = [0,1,2,2,3,0,4,2], val = 2 输出:5, nums = [0,1,4,0,3] 解释:函数应该返回新的长度5 并且 nums 中的前五个元素为 0,1,3,0,4。注意这五个元素可为任意顺序。你不需要考虑数组中超出新长度后面的元素。
思路一:暴力解法
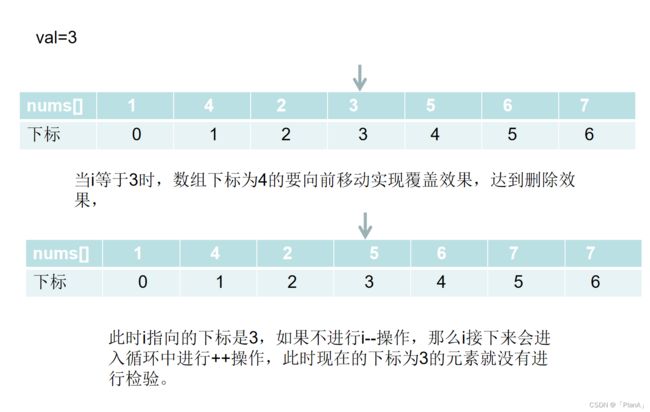
让我们找到对应的val值并删除,我们可以先用一个for循环,判断数组中的值是否有与val相等的如果有,我们可以用后一个数据元素覆盖前一个元素实现覆盖效果,注意,我们覆盖了一次以后。后面的元素都要向前移动一个位置,要再次使用一个for循环,也就是要使用两个for循环。需要注意的时我们以下的方法,都是实现覆盖效果,最后一个元素没有做处理。
动态效果:
代码实现:
(c语言)
int removeElement(int* nums, int numsSize, int val) {
int i,j;
for(i=0;i第二个for循环后面为什么要执行i--操作呢?
思路二:双指针
什么是双指针呢?
双指针指的是在算法中使用两个指针来解决问题的一种技巧。这两个指针可以是在同一数组中移动的两个指针,也可以是在不同数组中移动的两个指针。
在算法中,双指针技巧通常用于处理涉及数组、链表或字符串的问题。通过使用双指针,我们可以更有效地解决一些问题,降低时间复杂度或空间复杂度。
双指针常见的应用场景有:
快慢指针:例如在链表中判断是否存在环或找到环的入口点时,可以使用快慢指针。快指针每次移动两步,慢指针每次移动一步,如果链表中存在环,则快指针最终会追上慢指针。
对撞指针:对于已排序的数组或链表,可以使用左右两个指针从两端向中间移动,以解决一些查找问题或判断问题。例如,在已排序的数组中查找两个数之和为目标值的问题,可以使用左右指针向中间移动并进行比较。
滑动窗口:滑动窗口是一个固定大小的窗口,在数组或字符串上滑动。它通常用于解决一些子串或子数组的问题。我们可以使用双指针分别表示窗口的左右边界,通过移动指针来调整窗口的大小或位置。
使用双指针技巧时,需要注意指针的移动规则和退出条件,确保算法的正确性和高效性。双指针技巧可以帮助我们解决一些复杂的问题,提高算法的效率。
解决这个问题我们就可以用到快慢指针,块指针用来寻找新数组中的元素(就是找出不等于val的值,慢指针就是用来记录新数组的下标.
动态效果:
代码实现
(c语言)
int removeElement(int* nums, int numsSize, int val) {
int fast=0;//快指针
int slow=0;//慢指针
for(fast=0;fast(Java):
class Solution {
public int removeElement(int[] nums, int val) {
int i=0;
int j=0;
for(j=0;j二 【二分查找】
原题链接:704. 二分查找 - 力扣(LeetCode)
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums= [-1,0,3,5,9,12], target= 9输出: 4
解释: 9 出现在 nums中并且下标为 4
示例 2:
输入: nums= [-1,0,3,5,9,12], target= 2输出: -1
解释: 2 不存在 nums中因此返回 -1
二分查找是一种高效的查找算法,也称为折半查找。它适用于已排序的数组或列表。其基本思想是每次将查找区间缩小为原来的一半,通过与目标值的比较,确定目标值是否在缩小后的区间内,从而最终找到目标值或确定不存在。
以下是二分查找的详细步骤:
确定查找区间的起始和结束位置。通常,初始时起始位置为数组的第一个元素的索引,结束位置为数组的最后一个元素的索引。
计算查找区间的中间位置。可以使用公式
mid = (start + end) / 2来计算中间位置。比较中间位置的元素与目标值的大小:
- 如果中间位置的元素等于目标值,表示找到了目标值,返回中间位置。
- 如果中间位置的元素大于目标值,表示目标值可能在左半部分,将结束位置更新为中间位置减一,继续进行下一轮查找。
- 如果中间位置的元素小于目标值,表示目标值可能在右半部分,将起始位置更新为中间位置加一,继续进行下一轮查找。
重复步骤 2 和步骤 3,直到找到目标值或确定不存在。如果起始位置大于结束位置,则表示目标值不存在。
二分查找的时间复杂度是 O(log n),其中 n 是数组或列表的长度。它是一种高效的查找算法,但要求在查找之前需要对数组或列表进行排序。如果数据是动态变化的,频繁进行插入、删除操作,就不适合使用二分查找。
动态效果
代码实现
int search(int* nums, int numsSize, int target){
int low=0;
int high=numsSize-1;
int midle;
while(low<=high){
midle=(low+high)/2;
if(target>nums[midle]){
low=midle+1;
}else if(target三 【有序数组的平方】
原题链接:977. 有序数组的平方 - 力扣(LeetCode)
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
示例 1:
输入:nums = [-4,-1,0,3,10]
输出:[0,1,9,16,100]
解释:平方后,数组变为 [16,1,0,9,100]
排序后,数组变为 [0,1,9,16,100]
示例 2:输入:nums = [-7,-3,2,3,11]
输出:[4,9,9,49,121]
思路一:直接排序
先将数组中的每一个元素进行平方,然后结合各种排序算法实现。
【代码实现】
class Solution {
public int[] sortedSquares(int[] nums) {
int[] a = new int[nums.length];
for (int i = 0; i < nums.length; ++i) {
a[i] = nums[i] * nums[i];
}
Arrays.sort(a);
return a;
}
}
思路二:双指针
对撞指针也被称为双指针法或双指针技巧,是一种在数组或列表中使用两个指针进行遍历的算法技巧。这两个指针通常分别位于数组或列表的起始位置和结束位置,通过向中间移动指针,以解决一些问题。
对撞指针通常用于已排序的数组或列表中,利用有序性质来解决问题。它的基本思路是通过移动两个指针,同时从数组的两端向中间逼近,缩小搜索范围或判断条件。
对撞指针的常见应用场景有:
查找问题:例如在有序数组中查找两个数之和为目标值的问题,可以使用两个指针从数组的两端向中间移动,根据两个指针指向的数之和与目标值的大小关系来调整指针的位置。
判断问题:例如判断一个字符串是否是回文字符串,可以使用两个指针从字符串的两端向中间移动,同时比较两个指针指向的字符是否相等。
反转问题:例如反转数组或列表中的元素,可以使用两个指针从数组或列表的两端向中间移动,并交换两个指针指向的元素。
对撞指针的特点是指针的移动方向相反,且指针遍历的范围逐渐缩小。使用对撞指针可以在一次遍历的过程中解决问题,从而提高算法的效率。需要注意的是,在使用对撞指针时,需要定义好指针的起始和结束位置,并控制好指针的移动条件,确保算法的正确性。
解决这个问题我们用到对撞指针,也就是一个指针在数组的末端,一个在起始端两个向中间移动。因为数组是有序的,所以我们主要的问题就是负数的平方的大小的问题,所以我们用i指向开头,j指向末尾,这时比较i与j对应的数据的平方,然后将大的数据放入新数组的末端,依次进行下去。
动态效果:
【代码实现】
int* sortedSquares(int* nums, int numsSize, int* returnSize) {
int i,j;
int k=numsSize-1;
int *result = (int *)malloc(numsSize * sizeof(int));
for(i=0,j=numsSize-1;i<=j;k--){
if(nums[i]*nums[i]>=nums[j]*nums[j]){
result[k]=nums[i]*nums[i];
i++;
}else{
result[k]=nums[j]*nums[j];
j--;
}
}
*returnSize = numsSize;
return result;
}四 【长度最小的子数组】
原题链接:LCR 008. 长度最小的子数组 - 力扣(LeetCode)
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2:输入:target = 4, nums = [1,4,4]
输出:1
示例 3:输入:target = 11, nums = [1,1,1,1,1,1,1,1]
输出:0
思路一:暴力解法
class Solution {
public int minSubArrayLen(int target, int[] nums) {
int result = Integer.MAX_VALUE; // 最终的结果
int sum = 0; // 子序列的数值之和
int subLength = 0; // 子序列的长度
for (int i = 0; i < nums.length; i++) { // 设置子序列起点为i
sum = 0;
for (int j = i; j < nums.length; j++) { // 设置子序列终止位置为j
sum += nums[j];
if (sum >= target) { // 一旦发现子序列和超过了s,更新result
subLength = j - i + 1; // 取子序列的长度
result = result < subLength ? result : subLength;
break; // 因为我们是找符合条件最短的子序列,所以一旦符合条件就break
}
}
}
// 如果result没有被赋值的话,就返回0,说明没有符合条件的子序列
return result == Integer.MAX_VALUE ? 0 : result;
}
}思路二:滑动窗口
我们让终止位置j在数组中向前滑动,当满足数组中的元素加起来大于目标值时,起始位置开始移动缩小范围,同时每次记录下最小的长度,不断比较。
动态效果:(以题目中例1为例)
【代码实现】
C:
int minSubArrayLen(int target, int* nums, int numsSize){
int i=0;//起始指针
int j=0;//终止指针
int result=2147483647;
int sum=0;
int l;//记录满足要求的子数组长度
for(j=0;j=target){
l=j-i+1;
result=result Java:
class Solution {
// 滑动窗口
public int minSubArrayLen(int s, int[] nums) {
int left = 0;
int sum = 0;
int result = Integer.MAX_VALUE;
for (int right = 0; right < nums.length; right++) {
sum += nums[right];
while (sum >= s) {
result = Math.min(result, right - left + 1);
sum -= nums[left++];
}
}
return result == Integer.MAX_VALUE ? 0 : result;
}
}参考资料:
1.代码随想录 (programmercarl.com)
(强烈推荐新小白不会刷题的可以看这个结合B站代码随想录的课程)
2.力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台