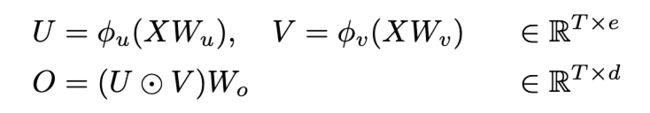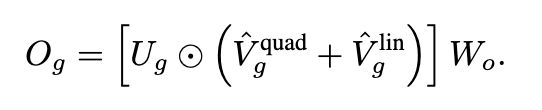FLASH:一种高效的Transformer设计
背景
近年来,Transformer凭借其优秀的设计,在文本、图像、语音等方向大杀四方。但是由于其attention的二次复杂度限制了其在长序列上的应用。本文提出了一种快(速度快)、省(省显存)的模型FLASH(Fast Linear Attention with a Single Head),在长序列的表现远远高于标准的Transformer。
模型介绍
GAU(Gated Attention Unit)
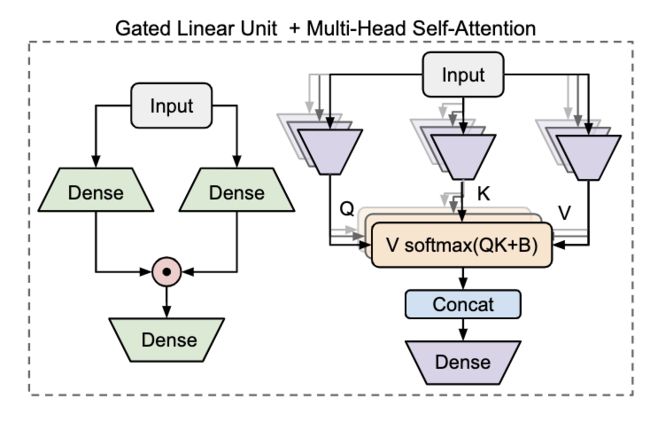
在标准的Transformer结构中,多头注意力和FFN是交替连接的。GLU那篇论文中,将FFN替换成基于门控的线性单元,发现效果会变好。因此,我们先简单了解一下门控单元GLU的计算,如下左图:
也就是将输入X分别经过放射变换(线性映射+激活函数)得到 U , V U,V U,V。然后再将 U , V U,V U,V进行点积,最后再进行线性映射,得到门控线性单元的输出。
上述的GLU中没有对token两两进行注意力计算,如果在上面的 U , V U,V U,V中引入注意力,那岂不是就省了前面的多头注意力计算了。如下式:
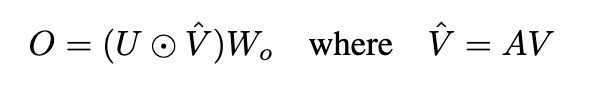
在 U , V U,V U,V进行点积计算的时候,如果给 V V V乘一个注意力矩阵 A A A(维度为nxn,其中n为序列的长度),那岂不是就引入了注意力信息。
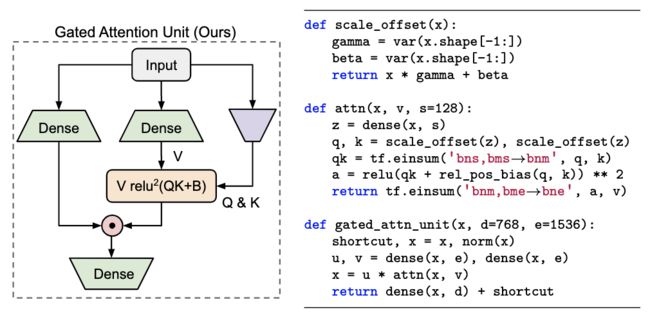
基于此,本文就提出了一种新的结构GAU。主要是给出了一种注意力矩阵A的计算方法。具体计算如下:
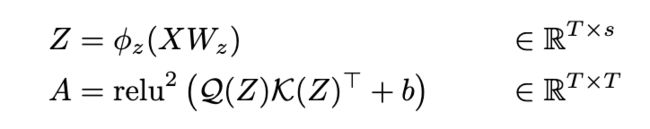
对输入X进行放射变换(线性映射+激活函数)得到Z,然后对Z分别进行 Q , K \mathcal{Q},\mathcal{K} Q,K变换,就是对Z中的每一个标量进行平移等运算。 这里的 Q , K \mathcal{Q},\mathcal{K} Q,K变化类似于LayerNorm中的 α , β \alpha, \beta α,β,是可训练的。 然后将两种变换的结果进行矩阵乘。最后再经过一个 r e l u 2 relu^2 relu2的激活函数( r e l u 2 relu^2 relu2是将relu的计算结果平方),得到最终的注意力矩阵。然后和门控注意力单元中的V进行相乘,这样就在门控注意力单元中引入了注意力信息。具体结果如下图所示:
注意:可能是GLU对attention的依赖没有那么强,因此,作者在实验中只用了一个注意力头。
在GAU的实验中,作者固定e=2d,那"n层Attention+n层FFN"的标准Transformer模型,对应的就是"2n层GAU"的新模型,即该模型为FLASH-Quad。其中Quad表明复杂度依然是二次的。即:FLASH的二次复杂度版本。
Fast Linear Attention with GAU
可能有读者发现,在上述的GAU中,你只是将attention和FFN合并起来,替代了标准的attention+FNN,并没有解决attention的二次复杂度呀?对,因此,作者提出了一种快速计算注意力的方法。
过去,在解决注意力的二次复杂度问题上,有两种主流方法: (1)将注意力计算稀疏化、(2)将注意力计算线性化。稀疏化即人为根据先验知识规定哪些token可以进行注意力计算(典型代表: Longformer、BigBird等)。线性化则是提出另外的方法,去逼近标准注意力的效果(典型代表: Linformer、Performer等),如下公式所示:
正常的注意力是将 Q , K Q,K Q,K进行矩阵乘,接着经过softmax,最后乘V。如果将K和V先进行乘,则可以大大减少计算量。假设 Q , K , V Q,K,V Q,K,V的维度为: ( m , d ) (m,d) (m,d),则标准注意力的计算量为:
m ∗ d ∗ m + m ∗ d ∗ m m*d*m+m*d*m m∗d∗m+m∗d∗m,即: 2 d m 2 2dm^2 2dm2,是跟序列长度m成平方正比。如果先算K乘V,则计算量为: d ∗ m ∗ d + d ∗ m ∗ d d*m*d+d*m*d d∗m∗d+d∗m∗d,即: 2 m d 2 2md^2 2md2,是跟序列长度m成一次正比。所以,第二种方法随着序列的边长,效率会远高于第一种方法。
本文则是根据上述两种方式,结合"稀疏化"和"线性化"的优点,提出了一种"局部+全局"的分块混合的注意力计算方法。
首先是分块注意力的计算,假设序列长度为n,每个块的维度为c,则可分成n/c个块(默认可整除)。 U g , V g ∈ R c × e , Z g ∈ R c × s \boldsymbol{U}_g,\boldsymbol{V}_g\in\mathbb{R}^{c\times e},\boldsymbol{Z}_g\in\mathbb{R}^{c\times s} Ug,Vg∈Rc×e,Zg∈Rc×s,其中g指的是第g个块。将 Z g \boldsymbol{Z}_g Zg通过四个放射变换(线性映射+激活)分别得到 Q g quad , K g quad , Q g lin , K g lin \boldsymbol{Q}_g^{\text{quad}},\boldsymbol{K}_g^{\text{quad}},\boldsymbol{Q}_g^{\text{lin}},\boldsymbol{K}_g^{\text{lin}} Qgquad,Kgquad,Qglin,Kglin。则块内注意力计算如下:
可以看出上述公式很好理解,不做过多描述。接下来算算其复杂度。每个块内注意力计算复杂度为 c 2 c^2 c2,有n/c个块,则块注意力计算整体的复杂度为: ( n / c ) ∗ c 2 (n/c) * c^2 (n/c)∗c2,即nc,也就是正比于n。
接着用 Q g lin , K g lin \boldsymbol{Q}_g^{\text{lin}},\boldsymbol{K}_g^{\text{lin}} Qglin,Kglin进行全局的attention计算。这里采用的是上述介绍的注意力线性化方法。计算如下:
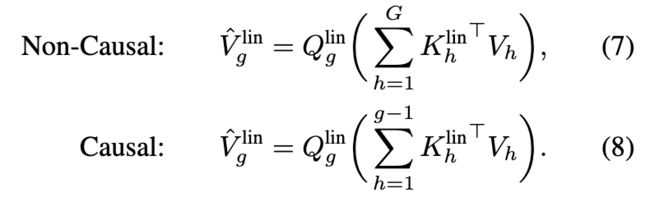
上述(7)式就是全局的两两计算。(8)式主要是在生成任务中,对标的是带有mask的多头注意力。
最后将两种attention结果整合到GAU中,得到线性版的GAU网络,计算如下:
作者在论文中还贴出来注意力计算的代码,如下所示:
至此,论文就介绍完了,下面简单看一下实验结果。
实验
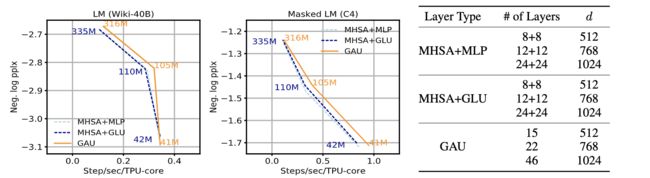
首先,作者对比了GAU、多头注意力+FFN、以及多头注意力+GLU三种结构,在自回归任务和MLM任务上的表现,如下图:
横轴为速度,纵轴为效果,越靠右上,效果越好。上述实验是在长度为512上的效果对比。可以发现,GAU的在相同效果的前提下,速度更快;在相同速度的前提下,效果更好。
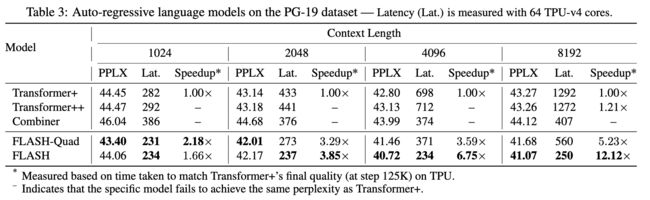
从上表中可以看出,虽然FLASH-Quad也是二次复杂度,但是也比标准的Transformer效果好,速度也更快。另外,随着序列的逐渐变长,FLASH的速度远远快于标准的Transformer。
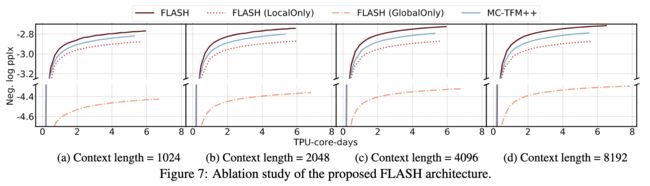
最后看看消融实验,如下图所示:
上面MF-TFM++模型采用的是多头注意力+FFN的结构,只是多头注意力采用的线性注意力+块注意力。也就是本文提出的注意力计算。从消融实验中,可以看出一个很有用的信息,即localOnly attention比GlobalOnly attention更重要。
本文参考:
[1] 论文: https://arxiv.org/abs/2202.10447
[2] GLU: https://arxiv.org/abs/2002.05202
[3] 苏剑林. (Feb. 25, 2022). 《FLASH:可能是近来最有意思的高效Transformer设计 》[Blog post]. Retrieved from https://kexue.fm/archives/8934