Leetcode并查集问题汇总
目录
Leetcode并查集问题汇总
1.什么是并查集
1.1 并查集的查找
1.2 并查集的合并
2.Leetcode并查集问题选做
2.1 547. 朋友圈
2.2 399. 除法求值
2.3 面试题 17.07. 婴儿名字
Leetcode并查集问题汇总
今天决定把并查集完全搞懂。
1.什么是并查集
在一些有 N 个元素的集合应用问题中,我们通常是在开始时让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中。这类题目特点是看似并不复杂,但数据量极大,若用正常的数据结构来描述的话,往往在空间上过大,计算机无法承受;即使在空间上勉强通过,运行的时间复杂度也很高,根本就不可能在比赛规定的运行时间内计算出试题需要的结果,只能采用一种全新的抽象的特殊数据结构——并查集。
并查集类似一个森林,每个结点均有一个 father[x]来表示x的父亲结点。
初始化集合x,集合中只有x一个元素,将x的根节点设置为它自身,这样每个集合的标号=根节点的标号。
public void init(int x){
father[x]=x;
}接下来看看并查集的两个重要操作:查找和合并。
1.1 并查集的查找
查找,即查找元素x所在的集合,即找到x的根节点的标号。
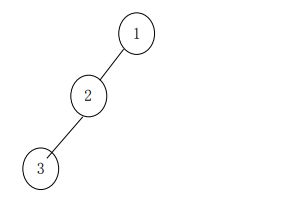
如图,如果我们想知道元素3所在的集合,我们可以知道father[3]=2,father[2]=1,我们就可以得到,元素3所在的集合为1。而且我们可以发现查找元素x所在的集合的运算次数=元素x所在的深度。
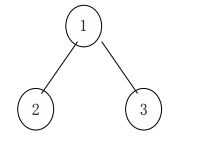
这里的查找有个路径压缩的优化,即得到 3 集合所在集合为 1 时,可以直接将 father[3] 设置为 1,而且在查找 3 时会查找 2,可能还会有其他的元素,将这些元素的 father通通都设置为 1,这样,下次查找 3 的子孙所在集合的时候,上例中,查找次数就都缩短了1. 当查找 3 的祖辈所在集合的时候,查找次数就都只为 1 了。路径压缩后集合变为:
我们可以这样编写代码:
//返回元素x所在的集合标号
public int find(int x){
//如果x不为根节点
if(x!=father[x]){
father[x]=find(father[x]);//路径压缩
}
return father[x];
}回溯时将所有递归的元素的 father[]均设置为集合根结点。此优化正是并查集的优势所在。
1.2 并查集的合并
union(x,y)即合并 x 和 y 所在的两个集合,我们只需要把其中一个集合的根结点设置为另一个集合根结点的孩子即可。
假设现在1,2,3三个节点,他们初始化就是三个仅包含他们自己的集合。
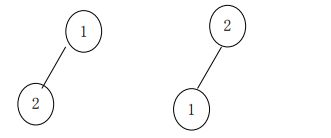
合并1和2,可以是:
这两种情况效果一样,但是如果再和3合并,可以是:
这两种情况会导致在查找元素3的集合的时候,前者的查找次数为2,后者的查找次数为1,后者的效率更高。所以并查集在合并时有一个启发式合并的优化,即记录每个集合的深度,当要合并两个集合时,将深度较小的集合挂在深度大的集合下面。(此优化效果不是很明显,作用不大,有时这样分情况讨论麻烦,也可直接将 y 挂到 x 上面)。
我们可以这么写代码:
//合并x和y所在的集合
public void union(int x, int y)
{
int fx = find(x);//找到x所在的集合,即x的根节点
int fy = find(y);//找到y所在集合,即y的根节点
if (fx == fy) return;
if (rank[fx] > rank[fy]) //y 合并到 x
{
father[fy] = fx;
if(rank[fy]+1>rank[fx])//如果挂上fy之后深度增加
{
rank[fx]=rank[fy]+1;//这里的秩为深度
}
}
else
{
father[fx] = fy;
if(rank[fx]+1>rank[fy]) rank[fy]=rank[fx]+1;
}
}并查集适用于所有集合的合并与查找的操作,进一步还可以延伸到一些图论中判断两个元素是否属于同一个连通块时的操作。由于使用启发式合并和路径压缩技术,可以将并查集的时间复杂度近似的看作 O(1),空间复杂度是 O(N),这样就将一个大规模的问题转变成空间极小、速度极快的简单操作。
2.Leetcode并查集问题选做
2.1 547. 朋友圈
班上有 N 名学生。其中有些人是朋友,有些则不是。他们的友谊具有是传递性。如果已知 A 是 B 的朋友,B 是 C 的朋友,那么我们可以认为 A 也是 C 的朋友。所谓的朋友圈,是指所有朋友的集合。
给定一个 N * N 的矩阵 M,表示班级中学生之间的朋友关系。如果M[i][j] = 1,表示已知第 i 个和 j 个学生互为朋友关系,否则为不知道。你必须输出所有学生中的已知的朋友圈总数。
示例 1:
输入:
[[1,1,0],
[1,1,0],
[0,0,1]]
输出:2
解释:已知学生 0 和学生 1 互为朋友,他们在一个朋友圈。
第2个学生自己在一个朋友圈。所以返回 2 。
示例 2:
输入:
[[1,1,0],
[1,1,1],
[0,1,1]]
输出:1
解释:已知学生 0 和学生 1 互为朋友,学生 1 和学生 2 互为朋友,所以学生 0 和学生 2 也是朋友,所以他们三个在一个朋友圈,返回 1 。
提示:
1 <= N <= 200
M[i][i] == 1
M[i][j] == M[j][i]
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/friend-circles
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。这是最典型、最简单的并查集问题,可以直接使用并查集求解。
//典型并查集问题
//我们使用father[N*N]数组来记录父节点,father[i]表示i的父节点
//一开始肯定有N个朋友圈即每个人他们自己,每合并一次,朋友圈数就会减少一次
class Solution {
public int[] father;
public int res;
public int findCircleNum(int[][] M) {
int N=M.length;
if(N<=0) return 0;
res=N;
father=new int[N*N];
//先给father数组全赋值-1
for(int i=0;i2.2 399. 除法求值
给出方程式 A / B = k, 其中 A 和 B 均为用字符串表示的变量, k 是一个浮点型数字。根据已知方程式求解问题,并返回计算结果。如果结果不存在,则返回 -1.0。
输入总是有效的。你可以假设除法运算中不会出现除数为 0 的情况,且不存在任何矛盾的结果。
示例 1:
输入:equations = [["a","b"],["b","c"]], values = [2.0,3.0], queries = [["a","c"],["b","a"],["a","e"],["a","a"],["x","x"]]
输出:[6.00000,0.50000,-1.00000,1.00000,-1.00000]
解释:
给定:a / b = 2.0, b / c = 3.0
问题:a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ?
返回:[6.0, 0.5, -1.0, 1.0, -1.0 ]
示例 2:
输入:equations = [["a","b"],["b","c"],["bc","cd"]], values = [1.5,2.5,5.0], queries = [["a","c"],["c","b"],["bc","cd"],["cd","bc"]]
输出:[3.75000,0.40000,5.00000,0.20000]
示例 3:
输入:equations = [["a","b"]], values = [0.5], queries = [["a","b"],["b","a"],["a","c"],["x","y"]]
输出:[0.50000,2.00000,-1.00000,-1.00000]
提示:
1 <= equations.length <= 20
equations[i].length == 2
1 <= equations[i][0].length, equations[i][1].length <= 5
values.length == equations.length
0.0 < values[i] <= 20.0
1 <= queries.length <= 20
queries[i].length == 2
1 <= queries[i][0].length, queries[i][1].length <= 5
equations[i][0], equations[i][1], queries[i][0], queries[i][1] 由小写英文字母与数字组成
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/evaluate-division
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。解答:
//本质上是一个带权并查集问题
//我们可以用一个哈希表father记录每个结点的父结点
//再用另一个哈希表values记录该结点到父节点的距离
//然后x,y方程式的解,也就是用x到根节点的距离除以y到根节点的距离
class Solution {
public HashMap father=new HashMap();
public HashMap values=new HashMap();
public double[] calcEquation(List> e, double[] v, List> q) {
//首先遍历一遍等式,顺便合并集合
for(int i=0;i temp=e.get(i);
String x=temp.get(0);
String y=temp.get(1);
//因为x,y肯定在同一个集合里,所以合并两个集合
union(x,y,v[i]);
}
//求结果
double[] res=new double[q.size()];
for(int i=0;i temp=q.get(i);
String x=temp.get(0);
String y=temp.get(1);
if(!father.containsKey(x) || !father.containsKey(y)){//要求解的方程元素没有
res[i]=-1;
continue;
}
String fx=find(x);//找x的父节点
String fy=find(y);//找y的父节点
if(!fx.equals(fy)) res[i]=-1;//如果x,y不在一个集合里,方程没解
else res[i]=values.get(x)/values.get(y);//否则解x到根节点的距离除以y到根节点的距离
}
return res;
}
//查找x的父节点
public String find(String x){
String fx=father.getOrDefault(x,x);//如果x没有父节点,那就是它自己,此时它自己就是根节点
String fx2=new String(fx);//记住它上一级的父节点
double vx=values.getOrDefault(x,1.0);
if(!fx.equals(x)){//如果它不是根节点,就继续回溯
fx=find(fx);//路径压缩
vx=vx*values.get(fx2);//x到根结点的距离
}
father.put(x,fx);
values.put(x,vx);
return fx;
}
//合并两个结点
public void union(String x,String y,double vi){
String fx=find(x);//找x的父节点
String fy=find(y);//找y的父节点
double vx=values.getOrDefault(x,1.0);
double vy=values.getOrDefault(y,1.0);
if(fx.equals(fy)) return ;//两个结点已经同集合了
father.put(fx,fy);//设置fy为fx的父节点
values.put(fx,vy*vi/vx);
}
} 2.3 面试题 17.07. 婴儿名字
每年,政府都会公布一万个最常见的婴儿名字和它们出现的频率,也就是同名婴儿的数量。有些名字有多种拼法,例如,John 和 Jon 本质上是相同的名字,但被当成了两个名字公布出来。
给定两个列表,一个是名字及对应的频率,另一个是本质相同的名字对。设计一个算法打印出每个真实名字的实际频率。注意,如果 John 和 Jon 是相同的,并且 Jon 和 Johnny 相同,则 John 与 Johnny 也相同,即它们有传递和对称性。
在结果列表中,选择字典序最小的名字作为真实名字。
示例:
输入:names = ["John(15)","Jon(12)","Chris(13)","Kris(4)","Christopher(19)"], synonyms = ["(Jon,John)","(John,Johnny)","(Chris,Kris)","(Chris,Christopher)"]
输出:["John(27)","Chris(36)"]
提示:
names.length <= 100000class Solution {
public String[] trulyMostPopular(String[] names, String[] synonyms) {
Map map = new HashMap<>();
Map father = new HashMap<>(); //并查集, key(子孙)->value(祖宗)
for (String name : names) { //统计频率
int idx1 = name.indexOf('(');
int idx2 = name.indexOf(')');
int frequency = Integer.valueOf(name.substring(idx1 + 1, idx2));
map.put(name.substring(0, idx1), frequency);
}
for (String pair : synonyms) { //union同义词
int idx = pair.indexOf(',');
String name1 = pair.substring(1, idx);
String name2 = pair.substring(idx + 1, pair.length() - 1);
while (father.containsKey(name1)) { //找name1祖宗
name1 = father.get(name1);
}
while (father.containsKey(name2)) { //找name2祖宗
name2 = father.get(name2);
}
if(!name1.equals(name2)){ //祖宗不同,要合并
int frequency = map.getOrDefault(name1, 0) + map.getOrDefault(name2, 0); //出现次数是两者之和
String trulyName = name1.compareTo(name2) < 0 ? name1 : name2;
String nickName = name1.compareTo(name2) < 0 ? name2 : name1;
father.put(nickName, trulyName); //小名作为大名的分支,即大名是小名的祖宗
map.remove(nickName); //更新一下数据
map.put(trulyName, frequency);
}
}
String[] res = new String[map.size()];
int index = 0;
for (String name : map.keySet()) {
StringBuilder sb = new StringBuilder(name);
sb.append('(');
sb.append(map.get(name));
sb.append(')');
res[index++] = sb.toString();
}
return res;
}
}