线性代数.笔记
第一章 行列式
1. 二阶、三阶行列式
a11 x a22 - a12 x a21的二阶行列式：
aij(i=1,2;j=1,2)称为行列式的元素或元
元素 aij的第一个下标 i称为行标，表明该元素位于第i行；第二个下标j称为列标，表明该元素位于第j列.位于第i行第j列的元素称为行列式（4）的（i，j）元
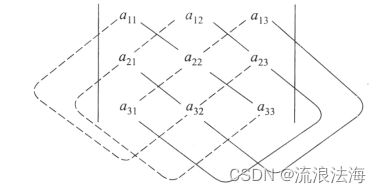
对角线法则
实连线称为主对角线，虚连线称为副对角线，于是二阶行列式便是主对角线上的两元素之积减去副对角线上两元素之积所得的差.（三阶行列式同样适用）
-------//-------
2. 全排列和对换
（1）.排列及其逆序数
把 n 个不同的元素排成一列，叫做这 n 个元素的全排列（也简称排列）.
对于 n 个不同的元素，先规定各元素之间有一个标准次序（例如 n 个不同的自然数，可规定由小到大为标准次序），于是在这 n 个元素的任一排列中，当某一对元素的先后次序与标准次序不同时，就说它构成 1 个逆序.一个排列中所有逆序的总数叫做这个排列的逆序数.
逆序数为奇数的排列叫做奇排列，逆序数为偶数的排列叫做偶排列.
（找寻排列数）例：
对换
在排列中，将任意两个元素对调，其余的元素不动，这种作出新排列的手续叫做对换.将
相邻两个元素对换，叫做相邻对换.
定理 1： 一个排列中的任意两个元素对换，排列改变奇偶性
推论 ： 奇排列对换成标准排列的对换次数为奇数，偶排列对换成标准排列的对换次数
为偶数.
--------//---------
3. n阶行列式的定义
对三阶行列式进行研究：经计算可知前三个排列都是偶排列，而后三个排列都是奇排列
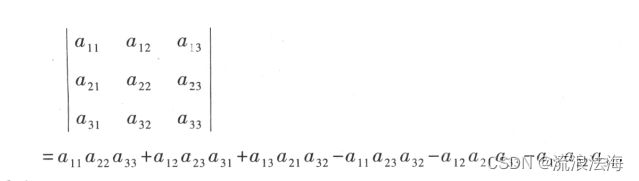
式右边的每一项都恰是三个元素的乘积，这三个元素位于不同的行、不同的列.因此式右端的任一项除正负号外可以写成 a1p1 a2p2 a3p3.这里第一个下标（行标）排成标准次序 123，而第二个下标（列标）排成p1p2p3，它是1，2，3 三个数的某个排列.这样的排列共有 6 种，对应式右端共含 6 项.
总之，三阶行列式可以写成
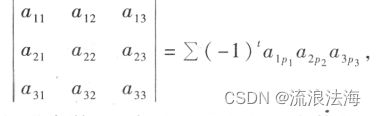
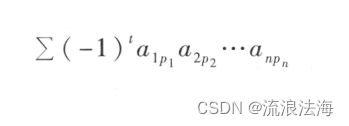
主对角线以下（上）的元素都为 0 的行列式叫做上（下）三角形行列式；特别，主对角线以下和以上的元素都为 0 的行列式叫做对角行列式.
-------//------
4. 行列式的性质
行列式 DT 称为行列式 D 的转置行列式.
性质 1： 行列式与它的转置行列式相等.
性质2： 对换行列式的两行（列），行列式变号
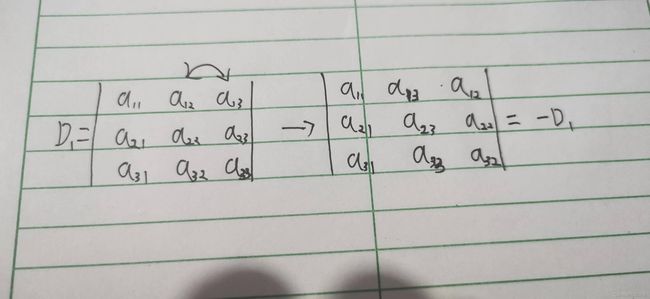
推论 如果行列式有两行（列）完全相同，则此行列式等于零.
即： D = - D，故 D = 0
性质3 行列式的某一行（列）中所有的元素都乘同一个数k，等于用数k乘此行列式
即：第 i行（或列）乘 k，等同于D x k；
推论 行列式中某一行（列）的所有元素的公因子可以提到行列式记号的外面.
性质4 行列式中如果有两行（列）元素成比例，则此行列式等于零.
性质5 若行列式的某一行（列）的元素都是两数之和，例如第i行的元素都是两数之和；
则 D 等于下列两个行列式之和：
性质6 把行列式的某一行（列）的各元素乘同一数然后加到另一行（列）对应的元素上去，行列式不变
例如以数 k 乘第i行加到第j行上
（记作 rj+kri），有
5. 行列式按行（列）展开
在 n 阶行列式中，把（i，j）元 aij所在的第 i行和第j列划去后，留下来的n-1阶行列式叫做（i，j）元aij的余子式，记作Mij记
Aij =（-1）i+jM ij；
Aij叫做（i，j）元aij的代数余子式.
引理 一个 n 阶行列式，如果其中第i行所有元素除（i，j）元 ai j外都为零，那么这行列式等于 aij与它的代数余子式的乘积，即
D = a ij A ij.
第二章 矩阵及其运算
1.线性方程组和矩阵
线性方程组
设有n个未知数，m个方程的线性方程组
其中 aij是第i个方程的第j 个未知数的系数，bi 是第 i个方程的常数项，i= 1，2，…，m；j= 1，2，…，n；当常数项 b1，b2，…，bm 不全为零时，线性方程组（1）叫做n元非齐次线性方程组，当b1，b2 …，bm全为零时，（1）式叫做n 元齐次线性方程组。
n 元线性方程组往往简称为线性方程组或方程组.
对于 n 元齐次线性方程组（2），x1 = x2 =… = xn = 0 一定是它的解，这个解叫做齐次线性方程组（2）的零解.如果一组不全为零的数是（2）的解，则它叫做齐次线性方程组（2）的非零解. 齐次线性方程组（2）一定有零解，但不一定有非
零解.
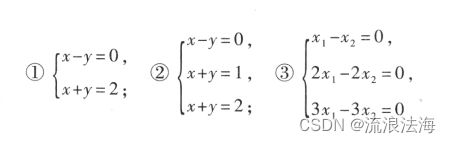
矩阵的定义
定义1 由 m×n 个数 aij（i= 1，2，…，m；j= 1，2，…，n）排成的 m 行 n 列的数表
称为m 行 n 列矩阵，简称m×n 矩阵.为表示它是一个整体，总是加一个括弧，并用大写黑体字母表示它，记作
这mxn个数称为矩阵A的元素，简称为元；
元素是实数的矩阵称为实矩阵；
元素是复数的矩阵称为复矩阵；
一般应用为实矩阵；
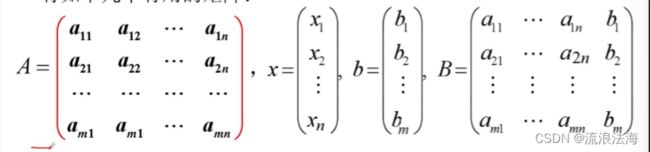
其中A称为系数矩阵，x 称为未知数矩阵，b 称为常数项矩阵，B 称为增广矩阵
矩阵的运算
矩阵的加法
定义 2 设有两个 m×n 阵 A =（aij）和 B =（bij），那么矩阵 A 与 B 的和记作 A +B，规定为
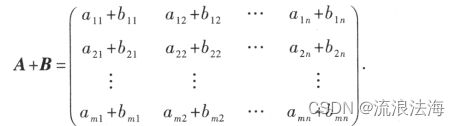
运算规律
交换律
结合律
其他
数与矩阵相乘
定义3：数λ与矩阵 A 的乘积记作λA 或 Aλ，规定为
运算规律
结合律
分配律