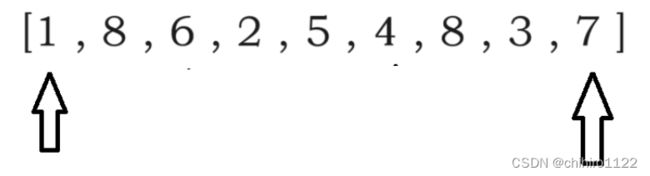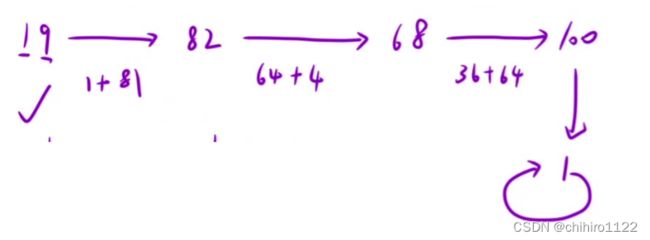C++ - 双指针_盛水最多的容器 - 快乐数 - 三数之和
盛水最多的容器
11. 盛最多水的容器 - 力扣(LeetCode)
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
示例 1:
输入:[1,8,6,2,5,4,8,3,7]
输出:49
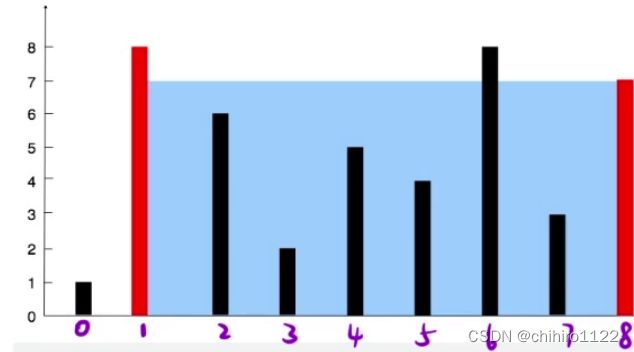
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。
在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。数组的长度是 高height,每一个数组都是一个边(墙壁),要求找两个数组(边),使得盛水最多,也就是要找出两个height最大的数组。
根据木桶效应,当我们往这个最大的容器当中注水,这个水的高度 height就是第二大的数组的长度。所以上述盛水最多的容器的体积就是 7 x 7 = 49。
即使 6 号数组的高度也是最高,我们选择 1 和 6 的话,计算出来的体积是 5 x 8 = 40 ,是小于 49 的,所以也不能选。
暴力解法
这道题的暴力解法还是非常简单的,无非就是找出 两个最长的数组,但是不是单单选出两个最长的数组,还要看两个数组之间距离,我们要的是 两个数组之间的距离 和 两个数组的小的那个的长度的乘积为最大。
利用两层 循环句可以搞定,外层固定一个数组,内层一次往后找数组,当有更大的出现,就记录这个更大体积和两数组的位置。
但是,这种解法不好,时间复杂度高。而且实现简单,这里就不实现了。
双指针
我们先随便取出一个区间来分析。
比如 6 2 5 4 这个区间,我们取 6 和 4 两个数组,此时一定可以计算出一个具体的体积:
h * w = v
那么此时,如果我们把 4 作为固定边,另一边向内枚举,那么 w 宽度一定是减少的。在此基础之上,我们来看高度的变化。
高度的变化有两种(如下图所示):
- 一种是 4 像内枚举的过程当中,找到一个 比 4 小的数,那么此时 的 h 高度就减少,那么 h 和 w 都减少,那就计算出来的体积一定是减少的。
- 第二种是 找到 一个 和 4 高度相等或者 比4 大的 数组,相等就不看了,大的话计算的高度是取 小的那个,也就是 4 的高度,那么此时,h 不变,但是 w 依旧减少,计算出的体积也一定是减少的。
那么,以 4 为固定边,向 6 ---- 4 区间之内 枚举 4 和 某一个数组的组合的话,计算出来的体积一定是 减少的,那么其中的例子也就不需要进行枚举了。我们可以大胆的把 这个 结点 干掉。
按照上述过程,我们就可以把区间放大,开始就是整个区间:
当计算出体积之后,就干掉小的那一个,然后往中间枚举就行了:
那么,当我们计算到 两个指针相遇的时候,一定算出了很多个 体积的值了,那么我们只需要选出最大的体积就行了。
代码实现:
class Solution {
public:
int maxArea(vector& height) {
int left = 0, right = height.size() - 1, ret = 0;
while(left < right)
{
// 计算体积
int v = (min(height[left], height[right])) * (right - left);
ret = max(ret, v);
if(height[left] < height[right])
{
left++;
}
else
{
right--;
}
}
return ret;
}
}; 快乐数
编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」 定义为:
- 对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。
- 然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。
- 如果这个过程 结果为 1,那么这个数就是快乐数。
如果 n 是 快乐数 就返回 true ;不是,则返回 false 。
示例 1:
输入:n = 19
输出:true
解释:
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1我们用 19 来分析:
19 是 快乐数,我们发现,计算到最后都会是 1 的旋转;
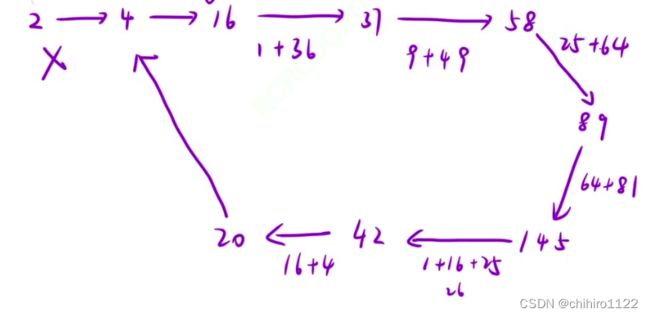
再用不是 快乐数的 数来分析:
我们发现,如果不是快乐数的话,它也会在其中,以其中的某一个数作为结点构成一个循环。
那么上述的这两种结构,就类似于是 循环链表这个题目,我们在 循环链表题目当中,判断一个链表是否带环,是用快慢指针来判断的,用一个 一次走一个结点的 slow 指针,和一个 一次走 两个结点的 fast 指针来判断。
如果链表当中带环的话,那么 两个指针往后遍历,肯定会走到 环当中,那么在一个无限循环的环当中,一个指针快,一个指针满,两个指针一定会相遇。所以我们使用 指针是否会相遇来判断一个链表是否带环。
那么上述的例子也是一样的,两种情况一定带环,说明两个指针一定会相遇。
如果是快乐数的话,循环当中的数都是1;如果不是的话,循环当中的数就不是1;
代码实现:
class Solution {
public:
int sum(int x)
{
int sum = 0;
while(x)
{
int mold = x % 10;
sum += mold * mold;
x /= 10;
}
return sum;
}
bool isHappy(int n) {
int left = n, right = sum(n);
while(left != right)
{
left = sum(left);
right = sum(sum(right));
}
return left == 1;
}
};三数之和
15. 三数之和 - 力扣(LeetCode)
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请
你返回所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
解释:
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意,输出的顺序和三元组的顺序并不重要。这里的 “答案中不可以包含重复的三元组”,意思就是 上述 的 [-1,0,1] 和 [0 , 1 ,-1] 这两组。虽然是利用不同的元素组合出来的,但是这两者重复的三元组。所以只能取一个。
暴力解法
暴力解法就是 暴力枚举,把每一种组合方式都列出出来,然后判断满足 三数之和的情况,然后在对满足的情况进行去重。
暴力枚举就不解释了,主要解释一下,去重的部分:
方式一:就是把每一个找出来的 三元组 都排个序,然后最后再来看有没有重复的三元组。
但是上述的方式比较的麻烦,因为一个数组当中可能会列出很多个 重复的三元组,那么我们在最后 来找这些相同的 三元组就会很麻烦,而且,对每一个三元组都排序,排序的效率可能就大于 我们使用排序的 时间复杂度了,因为有重复的三元组,相当于是对 大于 数组个数的元素进行排序。
所以,我们使用一种更好的方式,就是在找三元组之前,先把数组排好序,这样的话,在数组当中重复的元素就都在一起了。
我们发现,出现重复的三元组的原因在于,数组当中有重复的元素,那么我们就像把 重复 元素删除掉,这样在寻找三元组之后就不会再有重复的三元组了。
去重的话,C++ 当中有一个 set 容器,是利用 二叉搜索树 的底层来实现的,在插入元素的过程当中就会自动的进行去重。
当我们对数组进行排序之后,因为重复的元素都在一起了,所以此时我们在找出的重复三元组的结果是一样的:
重复的三元组,都是按照有序的方式进行组合的。
那么,我们就把组合出来的 三元组放到 set 容器当中,这样 set 容器就可以帮我们进行自动去重三元组。
当然,因为是暴力解法,所以时间复杂度肯定不高,而且我们还要对数组进行排序等等操作。
双指针
同样,要先对数组进行排序,排序之后,先固定一个数 a,然后在这个数的后面区间当中去利用双指针 求出找到 两数之和 为 -a 的情况。
需要注意的是,后续利用双指针找两数的时候,要注意不能找漏,当我们找到一组 两数 符合 规则,不能停下来要继续找。
还有,去重:
在 双指针的区间当中,如果 left 或者 right 已经找到一种 符合结果的三元组的了,当 left 或者 right 需要往中间迭代的时候,如果其中一个指针找到 和 迭代之前相同的元素,就不用进行对这个数的寻找了,可以跳过:
此时的 left 指向的是 0 ,0 已经和right 指向的元素的枚举过了,那么 此时 left 后面的 0 就没有必要在进行 枚举了,因为枚举出来的结果都一样,重复的。直接跳过就行。
而且,不止在双指针区间当中,在固定的数 i 也是一样的,当 i 的右边双指针区间 枚举完毕之后,i 是要往后迭代,但是如果 i 迭代之后,i 还是和原来的数 是一样的,那么枚举出的结果肯定也是一样的,所以就没有必要枚举了,直接跳过即可。
而且,因为数组的是有序的,所以当 i 指向的元素的值大于0 之后,右边就不可能有组合可以满足要求了。
left 一定是 小于 right的,这样可以防止越界。
双指针寻找的过程:
因为数组的是有序的,当在 区间当中找到的两数之和小于 -a ,说明 此时 left 的数太小, left++;如果 两数之和大于 -a,说明此时 right 的数太大,right--;
class Solution {
public:
vector> threeSum(vector& nums) {
vector> vv;
sort(nums.begin(), nums.end());
int i = 0;
int n = nums.size();
while(i < n)
{
int left = i + 1, right = n - 1;
int target = -nums[i];
while(left < right)
{
// 双指针判断
if(nums[left] + nums[right] < target)
{
left++;
}
else if(nums[left] + nums[right] > target)
{
right--;
}
else
{
vv.push_back({nums[i], nums[left], nums[right]});
left++;
right--;
// 去重 left 和 right
while(left < right && nums[left] == nums[left- 1]) left++;
while(left < right && nums[right] == nums[right + 1]) right--;
}
}
//去重i
i++;
while(i < n && nums[i] == nums[i - 1])i++;
}
return vv;
}
};