【经典算法题】单词搜索

【经典算法题】单词搜索

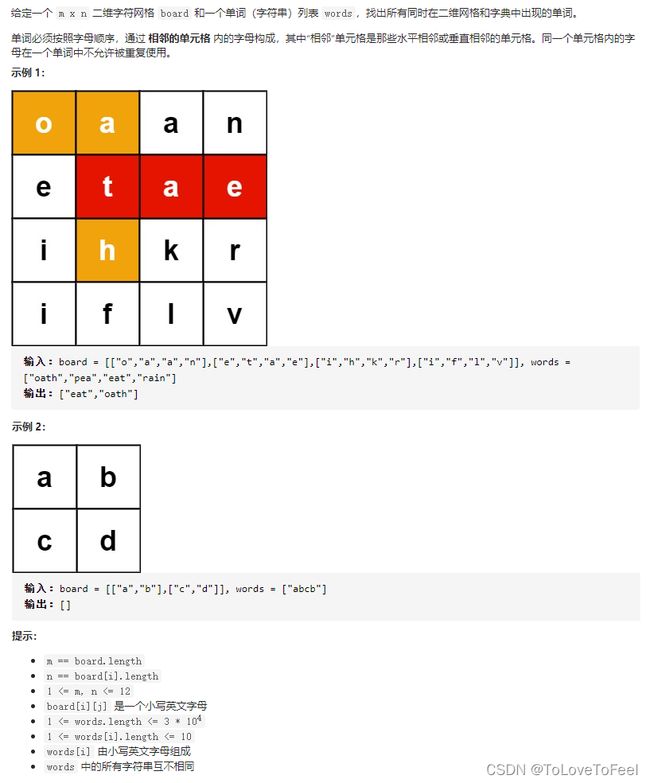
Leetcode 0079 单词搜索

题目描述：Leetcode 0079 单词搜索

分析

• 本题的考点：递归回溯。

• 首先我们枚举单词的起点，一共有$n\times m$个起点，然后从该起点开始暴搜，第一次最多有4个方向可以递归，之后最多有3个方向可以递归，因为不能往回搜。

• 确定起点后，对于该次暴搜，怎样保证我们不搜索之前已经搜索过的位置呢？我们可以将board中相应的位置变为一个特殊字符，比如.，表示已经被搜过了，之后回溯的时候再恢复即可。

代码

• C++

class Solution {
public:
    bool exist(vector<vector<char>>& board, string word) {

        for (int i = 0; i < board.size(); i++)
            for (int j = 0; j < board[0].size(); j++)
                if (dfs(board, word, 0, i, j)) 
                    return true;
        return false;
    }

    int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};

    // 从board[x][y]开始搜索word[u]
    bool dfs(vector<vector<char>> &board, string& word, int u, int x, int y) {

        if (board[x][y] != word[u]) return false;
        if (u == word.size() - 1) return true;

        char t = board[x][y];
        board[x][y] = '.';
        for (int i = 0; i < 4; i++) {
            int a = x + dx[i], b = y + dy[i];
            if (a < 0 || a >= board.size() || b < 0 || b >= board[0].size() || board[a][b] == '.')
                continue;
            if (dfs(board, word, u + 1, a, b)) return true;
        }
        board[x][y] = t;
        return false;
    }
};

• Java

class Solution {

    int[] dx = {-1, 0, 1, 0}, dy = {0, 1, 0, -1};

    public boolean exist(char[][] board, String word) {

        for (int i = 0; i < board.length; i++)
            for (int j = 0; j < board[0].length; j++)
                if (dfs(board, word.toCharArray(), 0, i, j))
                    return true;
        return false;
    }

    // 从board[x][y]开始搜索word[u]
    private boolean dfs(char[][] board, char[] word, int u, int x, int y) {

        if (board[x][y] != word[u]) return false;
        if (u == word.length - 1) return true;

        char t = board[x][y];
        board[x][y] = '.';
        for (int i = 0; i < 4; i++) {
            int a = x + dx[i], b = y + dy[i];
            if (a < 0 || a >= board.length || b < 0 || b >= board[0].length || board[a][b] == '.')
                continue;
            if (dfs(board, word, u + 1, a, b)) return true;
        }
        board[x][y] = t;
        return false;
    }
}

时空复杂度分析

• 时间复杂度：$O(n\times m\times 3^k)$，n、m为行数、列数，k为word长度。

• 空间复杂度：$O(k)$。

Leetcode 0212 单词搜索 II

题目描述：Leetcode 0212 单词搜索 II

分析

• 本题的考点：trie、递归回溯。

• 和Leetcode 0079 单词搜索的不同点在于，LC79只需要判断某一个单词是否存在即可，但是本题需要判断很多单词是否存在。因此可以将这些单词存入trie中，方便判断是否存在。

代码

• C++

class Solution {
public:
    struct Node {
        int id;
        Node *son[26];

        Node() {
            id = -1;
            for (int i = 0; i < 26; i++) son[i] = NULL;
        }
    } *root;

    unordered_set<int> ids;  // 存储能被搜到的单词的id
    vector<vector<char>> g;
    int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};

    void insert(string &s, int id) {
        auto p = root;
        for (auto c : s) {
            int u = c - 'a';
            if (!p->son[u]) p->son[u] = new Node();
            p = p->son[u];
        }
        p->id = id;
    }

    vector<string> findWords(vector<vector<char>> &board, vector<string> &words) {

        g = board;
        // 将单词放入trie中，方便之后判断单词是否存在
        root = new Node();
        for (int i = 0; i < words.size(); i++) insert(words[i], i);

        for (int i = 0; i < g.size(); i++) {
            for (int j = 0; j < g[0].size(); j++) {
                int u = g[i][j] - 'a';
                if (root->son[u])
                    dfs(i, j, root->son[u]);
            }
        }

        vector<string> res;
        for (auto id : ids) res.push_back(words[id]);
        return res;
    }

    // 从board[x][y]开始搜索以p为根的trie树中的单词
    void dfs(int x, int y, Node *p) {
        if (p->id != -1) ids.insert(p->id);
        char t = g[x][y];
        g[x][y] = '.';
        for (int i = 0; i < 4; i++) {
            int a = x + dx[i], b = y + dy[i];
            if (a >= 0 && a < g.size() && b >= 0 && b < g[0].size() && g[a][b] != '.') {
                int u = g[a][b] - 'a';
                if (p->son[u]) dfs(a, b, p->son[u]);
            }
        }
        g[x][y] = t;
    }
};

• Java

class Solution {
    static class Node {
        int id;
        Node[] son = new Node[26];

        Node() {
            id = -1;
            for (int i = 0; i < 26; i++) son[i] = null;
        }
    }

    Node root = new Node();
    HashSet<Integer> ids = new HashSet<>();  // 存储能被搜到的单词的id
    char[][] g;
    int[] dx = {-1, 0, 1, 0}, dy = {0, 1, 0, -1};

    void insert(String s, int id) {
        Node p = root;
        for (int i = 0; i < s.length(); i++) {
            int u = s.charAt(i) - 'a';
            if (p.son[u] == null) p.son[u] = new Node();
            p = p.son[u];
        }
        p.id = id;
    }

    public List<String> findWords(char[][] board, String[] words) {

        g = board;
        for (int i = 0; i < words.length; i++) insert(words[i], i);

        for (int i = 0; i < g.length; i++)
            for (int j = 0; j < g[0].length; j++) {
                int u = g[i][j] - 'a';
                if (root.son[u] != null)
                    dfs(i, j, root.son[u]);
            }

        List<String> res = new ArrayList<>();
        for (int id : ids) res.add(words[id]);
        return res;
    }

    // 从board[x][y]开始搜索以p为根的trie树中的单词
    void dfs(int x, int y, Node p) {
        if (p.id != -1) ids.add(p.id);
        char t = g[x][y];
        g[x][y] = '.';
        for (int i = 0; i < 4; i++) {
            int a = x + dx[i], b = y + dy[i];
            if (a >= 0 && a < g.length && b >= 0 && b < g[0].length && g[a][b] != '.') {
                int u = g[a][b] - 'a';
                if (p.son[u] != null) dfs(a, b, p.son[u]);
            }
        }
        g[x][y] = t;
    }
}

时空复杂度分析

• 时间复杂度：指数级别的。

• 空间复杂度：$O(n\times len)$，n为words中单词个数，len为单词平均长度。