Hash 表详解(哈希表)
给定表M,存在函数f(key),对任意给定的关键字值key,代入函数后若能得到包含该关键字的记录在表中的地址,则称表M为哈希(Hash)表,函数f(key)为哈希(Hash) 函数。
散列函数能使对一个数据序列的访问过程更加迅速有效,通过散列函数,数据元素将被更快地定位。
实际工作中需视不同的情况采用不同的哈希函数,通常考虑的因素有:
· 计算哈希函数所需时间
· 关键字的长度
· 哈希表的大小
· 关键字的分布情况
· 记录的查找频率
构造方法:
1. 直接寻址法:取关键字或关键字的某个线性函数值为散列地址。即H(key)=key或H(key) = a·key + b,其中a和b为常数(这种散列函数叫做自身函数)。若其中H(key)中已经有值了,就往下一个找,直到H(key)中没有值了,就放进去。
2. 数字分析法:分析一组数据,比如一组员工的出生年月日,这时我们发现出生年月日的前几位数字大体相同,这样的话,出现冲突的几率就会很大,但是我们发现年月日的后几位表示月份和具体日期的数字差别很大,如果用后面的数字来构成散列地址,则冲突的几率会明显降低。因此数字分析法就是找出数字的规律,尽可能利用这些数据来构造冲突几率较低的散列地址。
3. 平方取中法:取关键字平方后的中间几位作为散列地址。
4. 折叠法:将关键字分割成位数相同的几部分,最后一部分位数可以不同,然后取这几部分的叠加和(去除进位)作为散列地址。数位叠加可以有移位叠加和间界叠加两种方法。移位叠加是将分割后的每一部分的最低位对齐,然后相加;间界叠加是从一端向另一端沿分割界来回折叠,然后对齐相加。
5. 随机数法:选择一随机函数,取关键字的随机值作为散列地址,通常用于关键字长度不同的场合。
6. 除留余数法:取关键字被某个不大于散列表表长m的数p除后所得的余数为散列地址。即 H(key) = key MOD p,p<=m。不仅可以对关键字直接取模,也可在折叠、平方取中等运算之后取模。对p的选择很重要,一般取素数或m,若p选的不好,容易产生同义词。
处理冲突
1. 开放寻址法:Hi=(H(key) + di) MOD m,i=1,2,…,k(k<=m-1),其中H(key)为散列函数,m为散列表长,di为增量序列,可有下列三种取法:
1.1. di=1,2,3,…,m-1,称线性探测再散列;
1.2. di=1^2,-1^2,2^2,-2^2,⑶^2,…,±(k)^2,(k<=m/2)称二次探测再散列;
1.3. di=伪随机数序列,称伪随机探测再散列。
2. 再散列法:Hi=RHi(key),i=1,2,…,k RHi均是不同的散列函数,即在同义词产生地址冲突时计算另一个散列函数地址,直到冲突不再发生,这种方法不易产生“聚集”,但增加了计算时间。
3. 链地址法(拉链法)
4. 建立一个公共溢出区
查找过程中,关键码的比较次数,取决于产生冲突的多少,产生的冲突少,查找效率就高,产生的冲突多,查找效率就低。因此,影响产生冲突多少的因素,也就是影响查找效率的因素。影响产生冲突多少有以下三个因素:
1. 散列函数是否均匀;
2. 处理冲突的方法;
3. 散列表的装填因子。
散列表的装填因子定义为:α= 填入表中的元素个数 / 散列表的长度
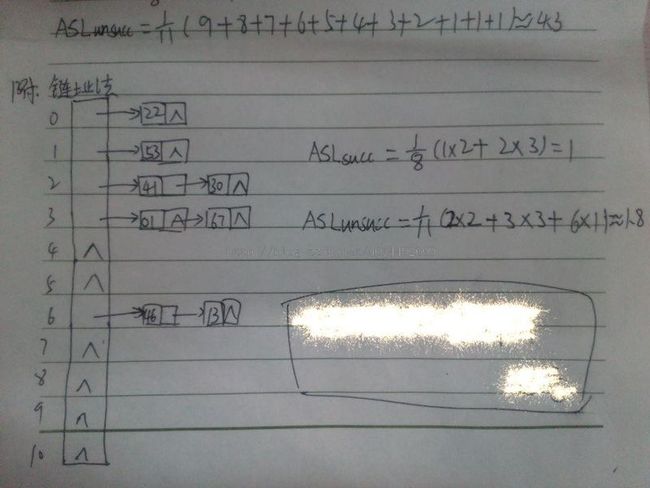
对于查找时成功与不成功的代码平均代码长度请看实例图:
普通代码:
#include<cstdio>
#include<cstdlib>
#define hashsize 6
#define NK -1
typedef struct{
int *elem;
int count;
}ht;
int m=0;
bool Init(ht *h)
{
int i;
m=hashsize;
h->count=m;
h->elem= (int*)malloc(m*sizeof(int));
for(i=0;i<m;i++)
h->elem[i]=NK;
return true;
}
int hash(int key)
{
return key%m;//hash函数,自定义
}
void Insert(ht *h,int key)
{
int addr = hash(key);
while(h->elem[addr]!=NK)//线性探测再散列法
addr = (addr+1)%m;
h->elem[addr] = key;
}
bool search(ht *h,int key)
{
int *addr=(int*)malloc(sizeof(int));
*addr = hash(key);
printf("dfgfdgfgfd\n");
while(h->elem[*addr]!=key)
{
*addr = (*addr+1)%m;
if(h->elem[*addr]==NK||*addr == hash(key))
{
return false;
}
}
return true;
}
int main()
{
int n,key;
ht h;
if(Init(&h))
printf("初始化完成!!!\n");
else
printf("初始化失败!!!\n");
scanf("%d",&n);//要存入hash表的数字量
for(int i=0;i<n;i++)
{
scanf("%d",&key);
Insert(&h,key);
}
scanf("%d",&key);//要查找的数字
if(search(&h,key))
printf("OK!\n");
else
printf("fail!\n");
return 0;
}
其实这个用不定长数组应该更简单的,今天就到这里,有时间补上vector代码。