机器学习(19)---神经网络详解
神经网络
- 一、神经网络概述
-
- 1.1 神经元模型
- 1.2 激活函数
- 二、感知机
-
- 2.1 概述
- 2.2 实现逻辑运算
- 2.3 多层感知机
- 三、神经网络
-
- 3.1 工作原理
- 3.2 前向传播
- 3.3 Tensorflow实战演示
-
- 3.3.1 导入数据集查看
- 3.3.2 数据预处理
- 3.3.3 建立模型
- 3.3.4 评估模型
- 四、反向传播
- 五、例题
-
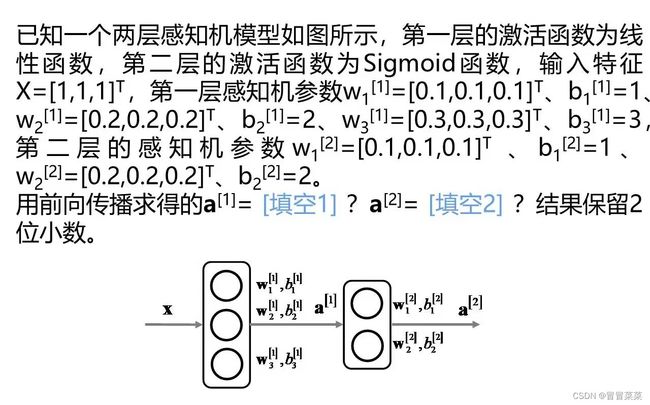
- 5.1 题1
- 5.2 题2
一、神经网络概述
1.1 神经元模型
1. 这里采用最广泛一种定义:神经网络是由适应性的简单单元组成的广泛并行互连的网络,它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应。
2. 定义中的 “简单单元” 是神经网络中最基本的成分,叫神经元模型。目前一直沿用至今的是 “M-P神经元模型”。
3. 在这个模型中,神经元接收到来自n个其他神经元传递过来的输入信号,这些输入信号通过带权重的连接(connection)进行传递,神经元接收到的总输入值与神经元的阈值进行比较,然后通过 “激活函数” 处理以产生神经元的输出。
1.2 激活函数
1. 神经网络中的激活函数是一种非线性函数,它被应用于神经元的输出,以便引入非线性特性。激活函数的作用是对输入信号进行转换,使其能够更好地适应复杂的数据模式。
2. 理想中的激活函数是阶跃函数,它将输入值映射为输出值“ 0 ”和“ 1 ”,显然 " 1 " 对应于神经元兴奋 " 0 " 对应于神经元抑制。然而阶跃函数具有不连续、不光滑等不太好的性质,因此常用Sigmoid函数作为激活函数。它把可能在较大范围内变化的输入值挤压到 (0,1) 输出值范围内,因此有时也称为 " 挤压函数 " (squashi functio)。

3. 不要在隐藏层中使用线性激活函数;通常在隐藏层中使用ReLu激活函数。
二、感知机
2.1 概述
1. 感知机 (Perceptron)由两层神经元组成,输入层接收外界输入信号后传递给输出层, 输出层是M-P神经元,亦称"阔值逻辑单元" (threshold logic unit)。
2.2 实现逻辑运算
1. 感知机能实现基本逻辑运算:与、或、非。 注意:需要我们选取正确的参数!
如下图所示:我们拿与来举例子,当x1和x2只有同时取1时,输出结果才会为1;如果有一个或者两个都取0,则输出结果为0,实现了与的逻辑运算。
2. 但是单层感知机不能实现异或运算。
2.3 多层感知机
1. 多层感知机有多层神经元,输出层与输入层之间的一层神经元,被称为隐居或隐含层(hidden laye),隐含层和输出层神经元都是拥有激活函数的功能神经元。
2. 多层感知机因为可以有多个隐层,所以可以实现异或运算。
3. 多层感知机有强大的表示能力,只需一个包含足够多神经元的隐层, 多层感知机就能以任意精度逼近任意复杂度的连续函数。多层感知机可以有多个隐层,每个隐层提取的特征不一样,越深(越靠近输出层)的隐层能够提取更高层的特征。
三、神经网络
3.1 工作原理
1. 原理可归结为:每一层输入一个数字向量并对其应用一堆逻辑回归单元,然后计算另一个数字向量(这一层的输出作为下一层的输入),然后从一层传递给另一层,直到到达最终的输出层。之后的输出结果可以进行预测也可以不进行预测。
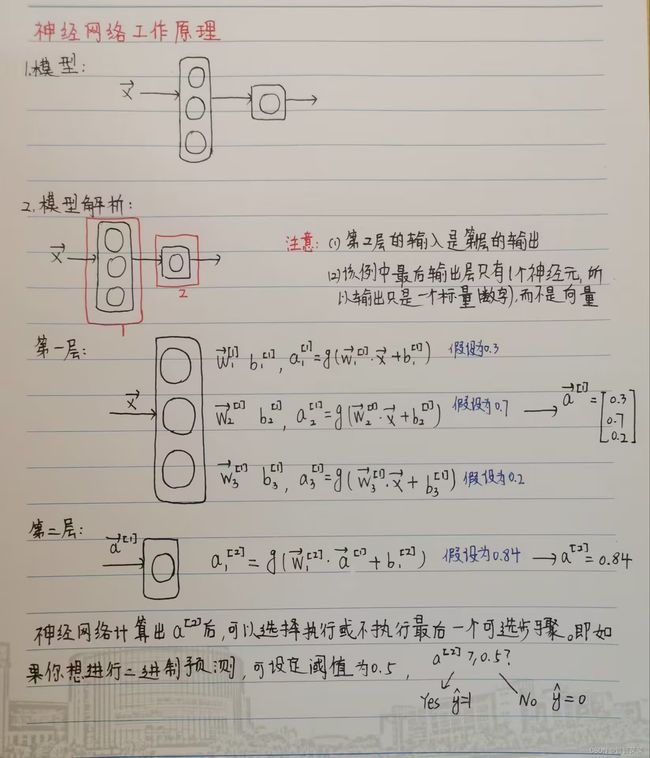
2. 简单神经网络模型的工作原理解析:
注:a、w、b右上角方括号里的数字代表是第几层,右下角数字表示是该层的第几个神经元。
3. 从简单到复杂,多层神经网络的工作原理和上叙是一样的。我们以一个四层网络为例子:
注:一般说到多层的神经网络时,它包括输出层和所有的隐含层,不包括输入层。
3.2 前向传播
神经网络在训练和计算时采用了前向传播的算法(从左往右)。
3.3 Tensorflow实战演示
3.3.1 导入数据集查看
MNIST数据集,由 60000 张训练图像和 10000 张测试图像以及表示图像中存在的数字的标签组成。每个图像由 28×28 个灰度像素表示,这里直接调用API即可。
import tensorflow as tf
import matplotlib.pyplot as plt
mnist = tf.keras.datasets.mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
# 查看整体情况
print("train_images shape: ", train_images.shape)
print("train_labels shape: ", train_labels.shape)
print("test_images shape: ", test_images.shape)
print("test_labels shape: ", test_labels.shape)
# 展示前9个图像
fig = plt.figure(figsize=(10, 10))
nrows = 3
ncols = 3
for i in range(9):
fig.add_subplot(nrows, ncols, i + 1) #行数、列数、索引
plt.imshow(train_images[i])
plt.title("Digit: {}".format(train_labels[i]))
plt.axis(False)
plt.show()
3.3.2 数据预处理
因为里面有数字,防止模型将数字当作数值处理,我们的目的是识别数字而非有大小之分的数值因此标记独一标签。
train_images = train_images / 255
test_images = test_images / 255
print("First Label before conversion:")
print(train_labels[0]) #5
# 转换成One-hot标签
train_labels = tf.keras.utils.to_categorical(train_labels)
test_labels = tf.keras.utils.to_categorical(test_labels)
print("First Label after conversion:")
print(train_labels[0]) #[0. 0. 0. 0. 0. 1. 0. 0. 0. 0.]
3.3.3 建立模型
1. 展平层:我们的输入图像是 2D 数组。展平层通过逐行解堆叠将 2D 数组(28 x 28 像素)转换为 1D 数组(像素)。该层只是更改数据形状,不会学习任何参数/权重,28*28=784;隐藏层:我们唯一的隐藏层由一个完全连接的节点(或神经元)密集层组成,每个节点(或神经元)都有激活功能,512relu;输出层:神经网络的输出层由一个具有 10 个输出神经元的密集层组成,每个神经元输出 10 个概率,每个概率为 0 – 9,表示图像是相应数字的概率。输出层被赋予激活函数,以将输入激活转换为概率,softmax。
2. 损失函数:这告诉我们的模型如何找到实际标签和模型预测的标签之间的误差。该指标衡量我们的模型在训练期间的准确性。我们希望模型最小化此函数值。我们将为我们的模型使用损失函数;优化:这告诉我们的模型如何通过查看数据和损失函数值来更新模型的权重/参数。我们将为我们的模型使用优化器adam;指标(可选):它包含用于监视训练和测试步骤的指标列表。我们将使用准确性或模型正确分类的图像数量。
### 设置图层
model = tf.keras.Sequential([
# 展平层
tf.keras.layers.Flatten(),
# 隐藏层
tf.keras.layers.Dense(units=512, activation='relu'),
# 输出层
tf.keras.layers.Dense(units=10, activation='softmax')
])
### 编译模型
model.compile(
loss = 'categorical_crossentropy',
optimizer = 'adam',
metrics = ['accuracy']
)
3.3.4 评估模型
1. 可视化损失性:
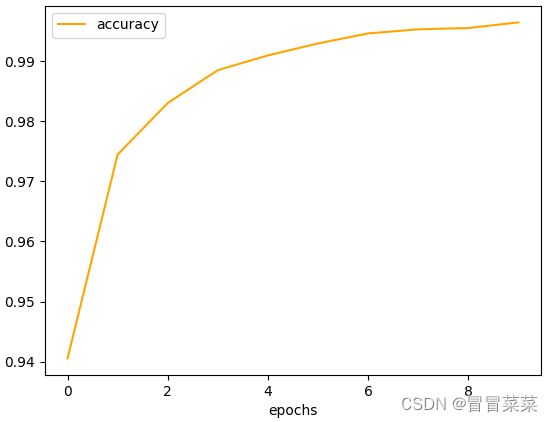
2. 可视化准确性:
四、反向传播
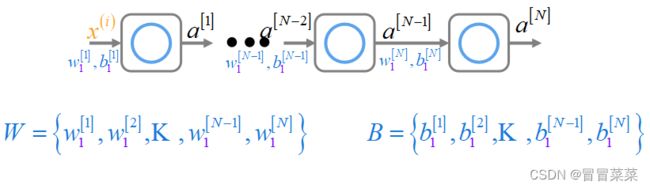
1. 这里我们采用每层1个单元的多层感知机做介绍。下图W和B中的K代表省略的值。
2. 反向传播计算中实际上是对每个参数求梯度下降。那求梯度下降关键是求损失函数对每个参数的偏导。
3. 推导过程:

4. 总结反向传播:从最后一层开始求每个参数的偏导,并将每层求得的部分偏导值(误差),反向传播给上一层,以方便求上一层参数的偏导。