【块状链表C++】文本编辑器（指针中 引用& 的使用）

》》》算法竞赛

/**
 * @file            
 * @author          jUicE_g2R(qq:3406291309)————彬(bin-必应)
 *						一个某双流一大学通信与信息专业大二在读	
 * 
 * @brief           一直在竞赛算法学习的路上
 * 
 * @copyright       2023.9
 * @COPYRIGHT			 原创技术笔记：转载需获得博主本人同意，且需标明转载源
 * @language        C++
 * @Version         1.0还在学习中  
 */

• UpData Log 2023.9.23 更新进行中
• Statement0 一起进步
• Statement1 有些描述是个人理解，可能不够标准，但能达其意

技术提升站点

20 块状链表

我认为叫 结点数组 比较好

20-1 背景

块状 的形成使用的就是 分块 的数据结构

分块使用到的 数组结构 可以极大的加速检索的效率

链表 使用的就是 基础数据结构 链

使用 链 这种结构 进行插入和删除等修改操作 就较数组 效率更高

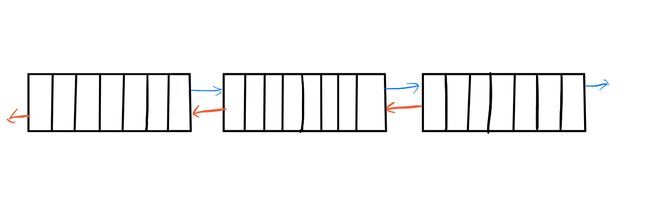
基于这两者各自的优势互补下，这种链表串起来的分块可以结合形成一种 检索很快，同时修改效率也很高的 高级数据结构 ：块状链表

20-2 实现

根据上图可知，这种数据结构的主体是链表，链上的结点（也就是一个分块）指向一个数组。

20-2-0 准备工作：指针芝士的储备

首先，这里涉及一个指针的芝士：

指针 * 、取地址 & 、解引用 *、引用 &

点击学习 指针、取地址、解引用、引用 相关知识

20-2-1 第一步：建立结构

• 动态链表 套 动态数组：就是 $list$ 套 $vector$

list<vector<char>> Link;                                        //Link是一条链，链上的 每一个结点 是 一个分块（分块 = 结点！！！）
typedef list<vector<char>>::iterator it;		                //重定义 迭代器（指针）类型的名字
int block_size=2500;                                            //分块的标准大小

20-2-2 第二步：获取信息

inline int Size(it node){return (node->size());}                //返回结点（分块）的大小
inline it  Next(it node){return ++node;}                        //返回下一个分块

20-2-3 第三步：定位

inline it Find(int& pos){                                       //查找（接收的是pos结点的值），由于又引用pos的地址，所有可以直接对pos的值操作！！！
    for(register it i=Link.begin();; i++){                      //i 是 用于遍历 链表上所有的结点 的指针
        if(i==Link.end() || pos<=Size(i))                       //i 处于所在的结点上 （遍历到末尾，不论如何都认定就在末尾结点 ）
            return i;
        pos-=(Size(i));                                         //遍历的最终目的是要获得 目标 在所处分块的排位
    }
}

20-2-4 第四步：对 结点（分块） 的操作

• 再分块操作

inline void Split(it node,int pos){                             //再分块操作：在 node 这个分块的 排位为pos处，将 块 一分为二（小块1，小块2）【pos位置划给小块2】
    if (pos==Size(node))                                        //如果 位置pos 是该分块的末尾，则无法进行再分块操作
        return;
    Link.insert(Next(node), vector<char>(node->begin()+pos, node->end()));  //把 小块2 分给 下一个分块
    node->erase(node->begin()+pos, node->end());                //清除 小块2（否则会出现重复的现象）
}

• 合并小块

inline void Merge(it node){
    node->insert(node->end(), Next(node)->begin(), Next(node)->end());      //在 前一个分块 的末尾 接上 下一个分块
    Link.erase(Next(node));									//清除 被合并的分块（否则会出现重复的现象）
}

• 维护链（块状链表 的 核心）

inline void Update(void){                                       //修改链上结点后，对链的状态进行更新
    for(register it i=Link.begin(); i!=Link.end(); i++){
        while(Size(i)>=(block_size<<1))                         //如果 分块 的大小 大于 两个block_size 则要再分块
            Split(i, Size(i) - block_size);
        while(Next(i) != Link.end() && Size(i)+Size(Next(i))<=block_size)   //（前提：下一个分块不是链的末尾）前后分块大小之和 比 block_size 小，则合并
            Merge(i);
        while(Next(i) != Link.end() && Next(i)->empty())        //清除最后一个空块 
            Link.erase(Next(i));                                    
    }
}

补充知识：.insert() 插入(方法)

//插入一个数：向 vector容器 的 pos位置(1) 插入一个数 val(0)
vector<int> arr{1,2};
arr.insert(1,0);			//.insert(pos, val)//{0,1,2}

//插入一串数：直接向 容器 的pos位置(2，即arr.end()) 插入另一个容器（或其中的部分）
vector<int> arr{1,2};	vector<int> ins{3,4,5};
arr.insert(arr.end(), ins.begin(). ins.end());//{1,2,3,4,5}

• 插入

inline void Insert(int pos, const vector<char>& ch){
    register it node=Find(pos);                                 //找到 目标 在所处分块的排位
    if(!Link.empty())                                           //必须保证 分块 不为空，否则没法进行 再分块 操作
        Split(node, pos);
    Link.insert(Next(node), ch);                                //把 字符 插入两个小块 之间
    Update();
}

• 删除

inline void Delete(int L, int R){								//两个Split处理的结果只是[L,R)，还需一步！！！
    register it node_l, node_r;
    //注：传入 Find函数中 的pos值 与 传入 Split函数 的pos值 不同 
    node_l=Find(L);     Split(node_l, L);
    node_r=Find(R);     Split(node_r, R);						//注：将 R-1对应的元素 划给 当前的node_r分块 ，而将 R对应的元素划给了 Next(node_r)分块！！！这点很多blog没写清楚
    node_r++;                                                   //右端点
    while(Next(node_l)!=node_r)                                 //将 node_l到node_r 的 结点依次清除
        Link.erase(Next(node_l));
    Update();
}

20-3 文本编辑器（HDU 4008）

题目描述

很久很久以前，$DOS3.x$ 的程序员们开始对 $EDLIN$ 感到厌倦。于是，人们开始纷纷改用自己写的文本编辑器⋯⋯

多年之后，出于偶然的机会，小明找到了当时的一个编辑软件。进行了一些简单的测试后，小明惊奇地发现：那个软件每秒能够进行上万次编辑操作（当然，你不能手工进行这样的测试） ！于是，小明废寝忘食地想做一个同样的东西出来。你能帮助他吗？

为了明确目标，小明对“文本编辑器”做了一个抽象的定义:

文本：由 $0$ 个或多个 ASCII 码在闭区间 [$32$, $126$] 内的字符构成的序列。

光标：在一段文本中用于指示位置的标记，可以位于文本首部，文本尾部或文本的某两个字符之间。

文本编辑器：由一段文本和该文本中的一个光标组成的，支持如下操作的数据结构。如果这段文本为空，我们就说这个文本编辑器是空的。

操作名称	输入文件中的格式	功能
$\text{Move}(k)$	Move k	将光标移动到第 $k$ 个字符之后，如果 $k=0$，将光标移到文本开头
$\text{Insert}(n,s)$	Insert n s	在光标处插入长度为 $n$ 的字符串 $s$，光标位置不变$n\ge 1$
$\text{Delete}(n)$	Delete n	删除光标后的 $n$ 个字符，光标位置不变，$n\ge 1$
$\text{Get}(n)$	Get n	输出光标后的 $n$ 个字符，光标位置不变，$n\ge 1$
$\text{Prev}()$	Prev	光标前移一个字符
$\text{Next}()$	Next	光标后移一个字符

你的任务是：

• 建立一个空的文本编辑器。

• 从输入文件中读入一些操作并执行。

• 对所有执行过的 GET 操作，将指定的内容写入输出文件。

输入格式

输入文件 editor.in 的第一行是指令条数 $t$，以下是需要执行的 $t$ 个操作。其中：

为了使输入文件便于阅读， Insert 操作的字符串中可能会插入一些回车符， 请忽略掉它们（如果难以理解这句话，可以参照样例） 。

除了回车符之外，输入文件的所有字符的 ASCII 码都在闭区间 [$32$, $126$] 内。且

行尾没有空格。

这里我们有如下假定：

• MOVE 操作不超过 $50000$ 个， INSERT 和 DELETE 操作的总个数不超过 $4000$，PREV 和 NEXT 操作的总个数不超过 $200000$。

• 所有 INSERT 插入的字符数之和不超过 $2M$（$1M=1024\times 1024$ 字节） ，正确的输出文件长度不超过 $3M$ 字节。

• DELETE 操作和 GET 操作执行时光标后必然有足够的字符。 MOVE 、 PREV 、 NEXT 操作必然不会试图把光标移动到非法位置。

• 输入文件没有错误。

对 C++ 选手的提示：经测试，最大的测试数据使用 fstream 进行输入有可能会比使用 stdio 慢约 $1$ 秒。

输出格式

输出文件 editor.out 的每行依次对应输入文件中每条 Get 指令的输出。

样例输入 #1

15
Insert 26
abcdefghijklmnop
qrstuv wxy
Move 15
Delete 11
Move 5
Insert 1
^
Next
Insert 1
_
Next
Next
Insert 4
.\/.
Get 4
Prev
Insert 1
^
Move 0
Get 22

样例输出 #1

abcde^_^f.\/.ghijklmno

#include
using namespace std;
const int N=1e3;
list<vector<char>> Link;                                        //Link是一条链，链上的 每一个结点 是 一个分块（分块 = 结点！！！）
typedef list<vector<char>>::iterator it;		                //重定义 迭代器（指针）类型的名字
int block_size=2500;                                            //分块的标准大小
inline int Size(it node){return (node->size());}                //返回结点（分块）的大小
inline it  Next(it node){return ++node;}                        //返回下一个分块
/*-----------------定位-----------------------------*/
inline it Find(int& pos){                                       //查找（接收的是pos结点的值），由于又引用pos的地址，所有可以直接对pos的值操作！！！
    for(register it i=Link.begin();; i++){                      //i 是 用于遍历 链表上所有的结点 的指针
        if(i==Link.end() || pos<=Size(i))                       //i 处于所在的结点上 （遍历到末尾，不论如何都认定就在末尾结点 ）
            return i;
        pos-=(Size(i));                                         //遍历的最终目的是要获得 目标 在所处分块的排位
    }
}

/*------------对 结点（分块） 的操作---------------------------*/
inline void Split(it node,int pos){                             //再分块操作：在 node 这个分块的 排位为pos处，将 块 一分为二（小块1，小块2）【pos位置划给小块1】
    if (pos==Size(node))                                        //如果 位置pos 是该分块的末尾，则无法进行再分块操作
        return;
    Link.insert(Next(node), vector<char>(node->begin()+pos, node->end()));  //把 小块2 分给 下一个分块
    node->erase(node->begin()+pos, node->end());                //清除 小块2（否则会出现重复的现象）
}
inline void Merge(it node){
    node->insert(node->end(), Next(node)->begin(), Next(node)->end());      //在 前一个分块 的末尾 接上 下一个分块
    Link.erase(Next(node));                                     //清除 被合并的分块（否则会出现重复的现象）
}

inline void Update(void){                                       //修改链上结点后，对链的状态进行更新
    for(register it i=Link.begin(); i!=Link.end(); i++){
        while(Size(i)>=(block_size<<1))                         //如果 分块 的大小 大于 两个block_size 则要再分块
            Split(i, Size(i) - block_size);
        while(Next(i) != Link.end() && Size(i)+Size(Next(i))<=block_size)   //（前提：下一个分块不是链的末尾）前后分块大小之和 比 block_size 小，则合并
            Merge(i);
        while(Next(i) != Link.end() && Next(i)->empty())        //清除最后一个空块 
            Link.erase(Next(i));                                    
    }
}

inline void Insert(int pos, const vector<char>& ch){
    register it node=Find(pos);                                 //找到 目标 在所处分块的排位
    if(!Link.empty())                                           //必须保证 分块 不为空，否则没法进行 再分块 操作
        Split(node, pos);
    Link.insert(Next(node), ch);                                //把 字符 插入两个小块 之间
    Update();
}
inline void Delete(int L, int R){								//两个Split处理的结果只是[L,R)，还需一步！！！
    register it node_l, node_r;
    //注：传入 Find函数中 的pos值 与 传入 Split函数 的pos值 不同 
    node_l=Find(L);     Split(node_l, L);
    node_r=Find(R);     Split(node_r, R);						//注：将 R-1对应的元素 划给 当前的node_r分块 ，而将 R对应的元素划给了 Next(node_r)分块！！！这点很多blog没写清楚
    node_r++;                                                   //右端点
    while(Next(node_l)!=node_r)                                 //将 node_l到node_r 的 结点依次清除
        Link.erase(Next(node_l));
    Update();
}

inline void Output(int L, int R){
    register it node_l=Find(L), node_r=Find(R);
    for(register it pi=node_l;; pi++){
        int first;     pi==node_l ? first=L : first=0;
        int last;      pi==node_r ? last=R  : last=Size(pi);
        for(int i=first; i<last;i++)                            //打印
            putchar(pi->at(i));
        if(pi==node_r)  break;                                  //遍历到右边界退出循环
    }  
}

int main(void){
    vector<char> ch;    int len,pos,n;
    cin>>n;
    while(n--){
        char op[7];     cin>>op;
        if(op[0]=='M')  cin>>pos;       //Move移动操作：将光标移动到第 k 个字符之后
        if(op[0]=='I'){                 //Insert插入操作：在光标处插入长度为 len 的字符串 s，光标位置不变 n>=1
            ch.clear(); cin>>len;   ch.resize(len);
            for(int i=0;i<len;i++){
                ch[i]=getchar();
                while((int)ch[i]<32 || (int)ch[i]>126)//循环直到读到合法数据
                    ch[i]=getchar();
            }
            Insert(pos, ch);
        }
        if(op[0]=='D'){ cin>>len;        Delete(pos, pos+len);} //Delete删除操作：删除光标后的 len 个字符，光标位置不变，n>=1
        if(op[0]=='G'){ cin>>len;        Output(pos, pos+len);} //输出光标后的 len 个字符，光标位置不变，n>=1
        if(op[0]=='P')  pos--;                                  //光标前移一个字符
        if(op[0]=='N')  pos++;                                  //光标后移一个字符
    }
    return 0;
}