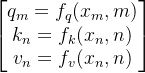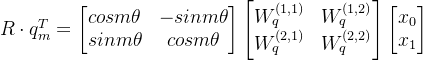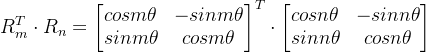LLM - 通俗理解位置编码与 RoPE
目录
一.引言
二.Why 位置编码?
三.What 绝对位置编码?
1.绝对位置编码
A.Embedding Table
B.公式计算
2.外推性
四.How 位置编码？
1.直接编号
2.乘法表示
3.严格的乘法表示
4.距离衰减
五.That's RoPE!
1.Self-Attention
2.RoPE 的复数形式
3.RoPE 的二维形式
4.RoPE 的多维形式
A.矩阵形式
B.图例形式
5.RoPE 的性质验证
A.严格的乘法表示
B.距离衰减
六.总结
一.引言
前面介绍 LLaMA-2 结构时，除了常规的 Embedding 层和 MLP 外，我们还看到了结构中包含的归一化层 RMSNormal，激活函数 SiLU 以及位置编码 RoPE，前两者的思想相对易于理解，而最后的 RoPE 则是相对晦涩，本文期望以最通俗的方式让大家对位置编码和 RoPE 有一个入门的认识。
二.Why 位置编码?
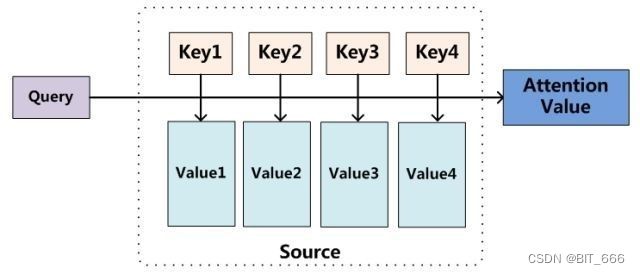
LLM 大语言模型中，最基础的就是 Token Embedding，针对 Query 中的每一个 Token，其都拥有对应的 Embedding 作为其表征。由于 Attention 的设计，网络感知不到 token 之间的位置关系。
以上图为例，每个 key 和 query 计算对应的相似度，由于 Query 是查找所有 Token 的向量并相加，所以调换 token 的顺序并不影响最终的 Query 向量，同理计算相似度并加权得到的 Attention Value 也不会受影响。而对于 LLM 对于自然语言，语序在自然理解中是很关键的元素，如果输入 '我喜欢你' 和输入 '你喜欢我' 输出相同的结果，显然无法接受。所以我们需要为 Query 的每个 token 引入其位置的表征，让 token 通过 '距离' 产生美。
三.What 绝对位置编码?
1.绝对位置编码
A.Embedding Table
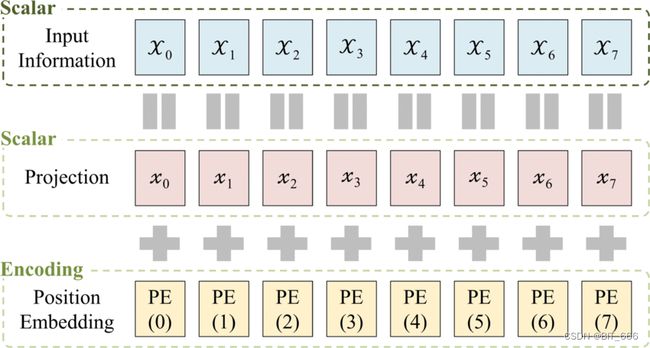
传统位置编码通过绝对位置为每个 token 对应的位置进行表征。以 Bert 为例，我们采用最简单最容易理解的位置编码即绝对位置编码，对于 token-i，其位置 pos=i：
具体实践中，我们会构建位置 i x emb_dim 的位置索引表 pos_emb，对于给定的 token-i，除了获取 token 对应的 text_emb 外，还会获取位置 i 对应的 pos_emd，二者相加得到叠加位置信息的 output embedding:
所以绝对位置编码信息通过增加一个 Position Embedding Table 的方式，为 token 引入了位置信息。
B.公式计算
Position Embedding 维度与上面的单词 Embeeding 维度相同，可以训练也可以使用公式计算，其传统计算公式为：
- pos 代表单词在句子中的位置
- d 标识 Position Embedding 的维度
- 2i、2i+1 标识偶数和奇数的维度
与上面类似，计算得到 PE 后与原 Embeeding 相加进入后续逻辑。
这里奇数和偶数位置的编码方法使用了正弦 sin 和余弦 cos 的不同的函数。这里奇数位置和偶数位置的区别在于他们所应用的正弦和余弦函数的角频率，通过调整角频率，可以使得奇数和偶数位置的编码方式有所不同。通过调整角频率，可以使得奇数和偶数位置编码的值在编码空间呈现不同的变化模式。这样的设计旨在为相邻位置提供不同的位置编码，以增加模型对序列中位置信息的敏感度。
2.外推性
外推性是指大模型由于训练和预测时输入的长度不一致，导致模型泛化能力下降的问题。例如我们训练的输入时最大使用了 512 个 token 的样本，而我们预测时输入超过 512 个 token，模型可能无法正确处理或者用 bak 方案得到较差的结果，这就限制了大模型处理长文本或者多轮对话等多 token 的场景，即对应模型不具备较好的外推性。
针对上面的绝对位置编码，如果训练中的 max_position 为 512，而测试出现 1024 长度的 position，针对 Position Embedding Table 有两种选择，第一种直接越界不存在对应位置 i 的 emb，报错退出；第二种 getOrElse 获取 bak_emb，此时超出 512 部分 token 的位置信息都是丢失的或者全部一致没有区分度，必然对模型效果造成影响。这里我想了一种 hash 的方式，可以一定程度减少位置信息的损失，但是还是会造成距离误判从而影响模型效果。
其次对于 Position Embedding Table，其维度是随着 max_position 线性增长的，假如 99.9% 的样本长度为 512，而有一批特殊样本的长度为 1024，为了适应新样本，Position Embedding Table 必须构建 1024 个索引，但是 512-1024 的索引训练和获取都是非常低频的，与此同时还会造成大量的内存占用，影响整体性能。
四.How 位置编码？
基于上面位置编码的思想，我们在 LLM 引入位置信息更像是构建特征工程，这里特征对应的信息就是 position，我们构建一个距离函数 f(x) 映射对应 Embedding Table，对每一个位置 i 映射获得其位置信息对应 Embedding Table 的 lookup，下面看看 f(x) 该具备怎样的性质。
1.直接编号
就像上面的绝对位置编码，根据 token-i 的位置 i 决定其对应的位置，映射为 f(x) = x，按照该方式可以轻易引入位置信息：
但是这个 f(x) 不好与 selt-attention 结合，因为向量之间做内积乘法，减法显然无法接受。
2.乘法表示
既然减法不满足需要乘法，那我们尝试乘法的性质构建距离函数 f(x)，更一般的：
乍一看好像没毛病了，但是再细细一看：
这家伙满足交换利，即 m-n 和 n-m 的距离是一样的，如果是数学意义里的 L1、L2 距离，似乎也没问题，但是关联到 NLP 领域这是不可接受的，如果我们引入的位置函数 f(x) 具备上述性质，则按照开头提到的示例:
query1: '我喜欢你'
query2: '你喜欢我''我' 和 '你' 分别对应 token-0 和 token-3，很明显两个 query 具备不同的含义，但是交换律成立的话二者将具备等同效应。
3.严格的乘法表示
内积的方式限定了我们的计算方式只能为乘法，但是乘法的交换律又使得我们无法处理样本的语义失真，因此我们需要细化 f(x)，使得 f(x) 不仅需要满足:
且不满足交换律：
◆ 向量乘法
对于位置 m、n 的 token，V(m)、V(n) 对应其位置向量：
不可以，向量点积乘法也满足交换律。
◆ 矩阵乘法
对于位置 m、n 的 token，R(m)、R(n) 为其对应位置矩阵：
Rm = np.array([[1, 2],
[3, 4]])
Rn = np.array([[3, 4],
[5, 6]])
print(np.dot(Rm, Rn))
print(np.dot(Rn, Rm))从上面的实例我们也可以看出，一般而言，矩阵 Rm * Rn 相乘不满足交换律，即：
因此矩阵的乘法性质满足我们上面不断严苛的条件，顺利进入我们的视野。
4.距离衰减
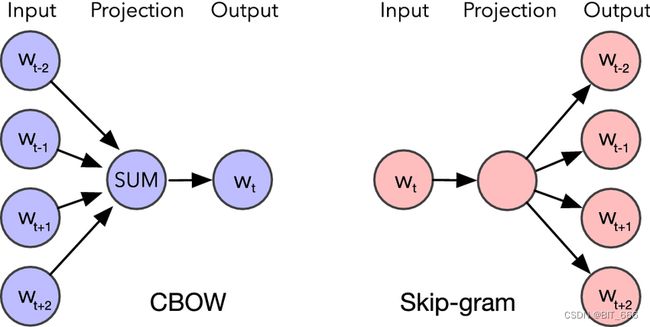
除了上面提到的性质，作为 NLP 的距离函数，f(x) 还应该满足距离的衰减性。对于文本 query 中不同位置的 token，距离远的两个 token 的乘积应该较小，而距离近的两个 token 的乘积结果应该较大，这比较符合我们人类自然语言的习惯，即相近的文字关联性更强。就像 word2vec 一样，我们选取 N-Gram 作为当前中心词的 Positive Label：
五.That's RoPE!
通过上面的分析，我们已经找到了距离函数 f(x) 的雏形，函数应该是一个盖世矩阵，有一天他会驾着七彩祥云来 LLM 实现位置编码：
于是就有了苏剑林老师提出的 RoPE (Rotary Position Embedding) 旋转位置编码。RoPE 的核心思想就是用相对位置来表示绝对位置。
1.Self-Attention
介绍 RoPE 之前，这里还是再啰嗦一下 Self-Attention 的流程，以供后面的知识更直观的理解。假设当前输入一个长度为 N 的 Query:
其中每个 Wi 代表 i 位置的 token，则通过 Token Embedding 查表后可得 QueryN 的 emb 表示：
其中 xi 表示位置 i 处的 token Wi 对应的 embedding。计算 Self-Attention 前，需要计算 Q、K、V，由于我们通过距离函数 f(x) 引入位置信息，所以对于位置 m、n 处的 token：
Attention 计算内积：
2.RoPE 的复数形式
经过上面分析，计算 QK.T 的内积时，由于我们引入 f(x)，所以应具备下述性质：
根据苏神提出的 RoPE，该变换为：
根据复数的特性有：
![\left \langle f(q, m),f(k,n) \right \rangle = Re[q_mk_n^*]](http://img.e-com-net.com/image/info8/13b8926aeeb04af19c1c4f1118d91ba7.png){kind=small}
将二维向量看做复数，其内积等于一个复数乘以另一个复数的共轭，结果再去实部，其中 Re 表示复数的实部，将上述变换带入可得：
![\left \langle q_me^{im\theta },k_ne^{in\theta } \right \rangle = Re[(q_me^{im\theta })(k_ne^{in\theta } )^*] = Re[q_mk_n^*e^{i(m-n)\theta }]](http://img.e-com-net.com/image/info8/50167d7f290947bbbb686af2c1231bef.png){kind=small}
经过一顿操作，引入距离信息的 q、k 内积结果依赖于 (m-n) 即二者 token 之间的相对位置。再回看开头提到的，RoPE 的核心思想就是用相对位置来表示绝对位置，我们在 f(q, m) 和 f(k, n) 中传入绝对位置信息，经过变换得到了二者关于相对位置 (m-n) 的信息。
3.RoPE 的二维形式
欧拉公式是复分析领域的公式，它将三角函数与复指数函数关联起来，因其提出者莱昂哈德·欧拉而得名，公式定义如下：
对于任意位置为 m 的二维向量
将上述式子转换为矩阵形式：
对应到 Self-Attention 中:
形式上相当于对 query 向量乘以旋转矩阵 R，在二维坐标系下对向量进行了旋转，因而上述位置编码方式命名为旋转位置编码。同理:
最终形式：
4.RoPE 的多维形式
A.矩阵形式
根据上面的结论，结合内积的线性叠加性，我们可以将 2 维的 R 推广到多维。相当于在原始 token 的向量上，两两截断通过 R 实现旋转操作，最后拼接为 R 维向量。犹如我们常用的向量维度都是偶数且是 2 的倍数，所以这里针对偶数向量：
![\Theta =\begin{Bmatrix} \theta _i=10000^{-2(i-1)/d},i\in [1,2,...,d/2]\end{Bmatrix}](http://img.e-com-net.com/image/info8/c89e9163c2fe47caa1be2489f02fb673.png){kind=small}
由于上述 R 矩阵的稀疏性，使用矩阵乘法会造成算力的严重浪费，所以推荐使用下述线性方式计算 RoPE:
其中 ⊗ 是逐位对应相乘，即 Numpy、Tensorflow 等计算框架中的∗运算。从这个实现也可以看到，RoPE 可以视为是乘性位置编码的变体，将多个二维旋转的叠加：
也就是说，给位置为 m 的向量 q 乘上矩阵 Rm，给位置为 n 的向量 k 乘上 Rn，用变换后的 Q、K 做 Attention，相乘得到的结果就包含位置信息了，因为上面的恒等式：
且 R 是一个正交矩阵，它不会改变向量的模长，因此通常来说它不会改变原模型的稳定性。
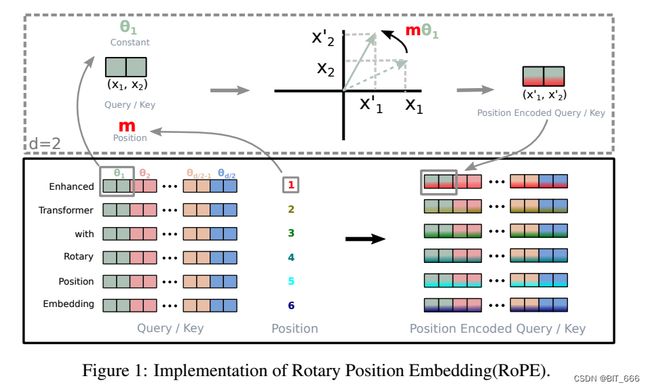
B.图例形式
因为上面的 
是两两表示的，所以实际计算中，也是将 token 词向量两两分成，这也解释了为什么公式里到处是 d/2。其添加位置信息步骤如下：
- 遍历每个位置的 token，位置为 m，范围为 Query / Key 的长度
- 获取对应 token Embedding，dim = d
- [2i: 2i+1] for i in range(0, d/2) 两两获取向量，根据公式计算 θ 并通过 R 进行旋转变换
- 得到新的 Position Encoded Query / Key
- Attention 操作并自动引入 (m-n) 的相对距离信息
从右上角的图中也可以更直观的看到向量旋转的过程。不过实际实现的代码中，与图中的实现步骤还是有一定出入，后续我们有时间会补上构造 RoPE 的代码分析详解，这里先给出论文中给出的简单示例供大家参考：
# You can implement the RoPE with a few lines of changes in the self-attention layer. Here we provide the pseudo code for instruction.
sinusoidal_pos.shape = [1, seq_len, hidden_size] # Sinusoidal position embeddings
qw.shape = [batch_size, seq_len, num_heads, hidden_size] # query hiddens
kw.shape = [batch_size, seq_len, num_heads, hidden_size] # key hiddens
cos_pos = repeat_elements(sinusoidal_pos[..., None, 1::2], rep=2, axis=-1)
sin_pos = repeat_elements(sinusoidal_pos[..., None, ::2], rep=2, axis=-1)
qw2 = stack([-qw[..., 1::2], qw[..., ::2]], 4)
qw2 = reshape(qw2, shape(qw))
qw = qw * cos_pos + qw2 * sin_pos
kw2 = K.stack([-kw[..., 1::2], kw[..., ::2]], 4)
kw2 = K.reshape(kw2, K.shape(kw))
kw = kw * cos_pos + kw2 * sin_pos
# Attention
a = tf.einsum('bjhd,bkhd->bhjk', qw, kw)5.RoPE 的性质验证
上面我们使用对称矩阵 R 进行了相关计算，下面验证下其相关性质。
◆ 和差化积公式
同时 sinx 为奇函数，cosx 为偶函数:
A.严格的乘法表示
旋转矩阵 R 形式如下:
计算交换律：
按照奇偶性我们可以轻松将 
的形式改变:
而:
即不满足交换律，不存在 token 位置对调语义相同的问题。
B.距离衰减
为了带来一定衰减性，RoPE 使用了 Sinusoidal 位置编码方案，令:
将 q、k 两两分组后，它们加上 RoPE 后的内积可用复数乘法表示为:
![(R_mq)^T(R_nk)=Re\begin{bmatrix} \sum _{i=0}^{d/2-1} q_{[2i:2i+1]}~k^*_{[2i:2i+1]}e^{i(m-n)\theta_i } \end{bmatrix}](http://img.e-com-net.com/image/info8/70c9837fcba04f22a417b57adfca0a00.png){kind=small}
记:
![h_i=q_{[2i:2i+1]}~k^*_{[2i:2i+1]}](http://img.e-com-net.com/image/info8/05b7191b5b25458898760e9a043f1802.png){kind=small}
并约定 h(d/2) = 0, S(0) = 0，由 Abel 变换 [分部求和法] 可得：
![\sum _{i=0}^{d/2-1} q_{[2i:2i+1]}~k^*_{[2i:2i+1]}e^{i(m-n)\theta_i } =\sum h_i(S_{i+1}-S_i)](http://img.e-com-net.com/image/info8/eb9037c5e65e4d7186fc75fcf5fd2bd0.png){kind=small}
所以：
![\begin{vmatrix} \sum _{i=0}^{d/2-1} q_{[2i:2i+1]}~k^*_{[2i:2i+1]}e^{i(m-n)\theta_i } \end{vmatrix} = \begin{vmatrix} \sum _{i=0}^{d/2-1} S_{i+1}(h_{i+1}-h_i) \end{vmatrix}](http://img.e-com-net.com/image/info8/e2bc716e22064474bb2e97b7b0060a67.png){kind=small}
将 max 部分视为常量，我们可以考察 ∑ 部分随着相对距离的变化情况作为衰减性的体现。苏神在论文中给出了对应的 Mathematica 代码，有兴趣的同学可以将上述代码转换为 Python 并 plot。
d = 128;
\[Theta][t_] = 10000^(-2*t/d);
f[m_] = Sum[Norm[Sum[Exp[I*m*\[Theta][i]], {i, 0, j}]], {j, 0, d/2 - 1}]/(d/2);
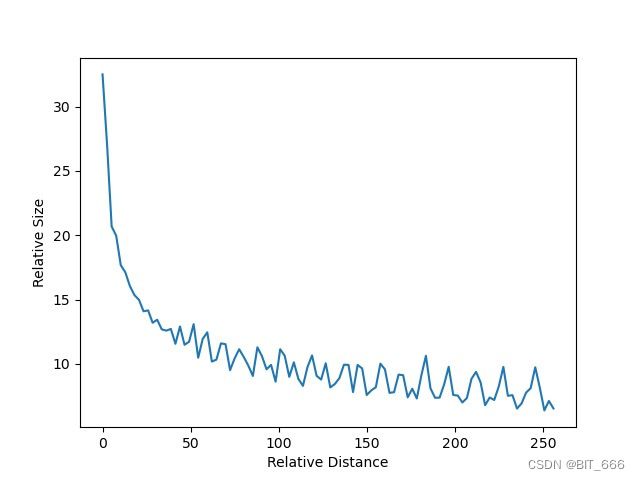
Plot[f[m], {m, 0, 256}, AxesLabel -> {相对距离, 相对大小}]d = 128 的衰减示意图：
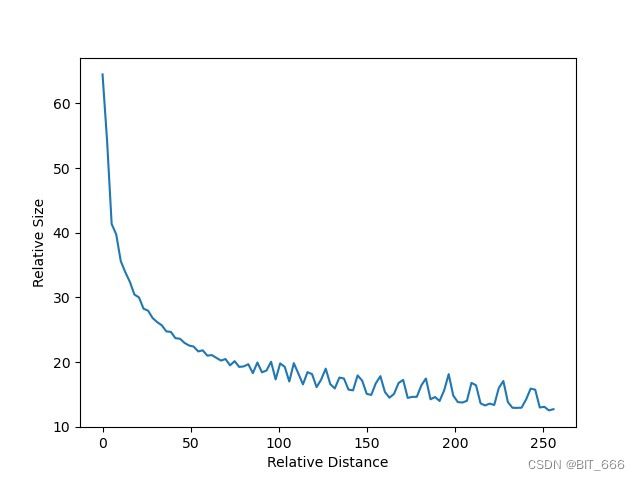
d = 256 的衰减示意图：
从图中我们可以看到随着相对距离的变大，内积结果有衰减的趋势，这符合我们自然语言的习惯，相近的词具有更高的关联程度，因此选择：
确实能够带来一定的远程衰减性。当然，能带来远程衰减性的不止这个选择，几乎任意的光滑单调函数都可以，这里只是沿用了已有的选择。苏神在论文中还尝试了以上述公式为 θ 初始化并训练 θi，发现训练一段时间参数并未显著更新，所以干脆固定为上述公式。
六.总结
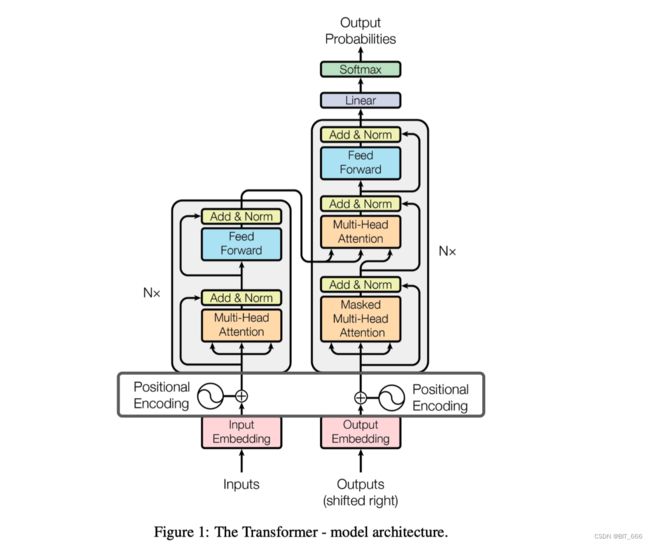
之前学习 Transformer ，了解相关 LLM 的模型多次看到位置编码、RoPE，每次总是一知半解，只知道加入位置编码有效但没有认真学习，这次也是参考了很多同学的分享，对 RoPE 有了进一步的认识。RoPE 实现了完整的理论到实践过程，而且在实践中被验证其有效性，目前主流大模型都有应用，例如 LLaMA、ChatGLM。当然，对于 RoPE 本文还有很多没有细致的点没有深入，例如完整的复函数的推理工程、位置编码与 β 进制的关系，下面也会给出苏神文章的链接，有兴趣的同学可以继续深入。本文中有疏漏的地方也欢迎大家指出~
最后感慨苏神的强大数学功底以及如此巧妙地设计了这套位置编码!
最后的最后，如果你对公式不感兴趣，对数学不感兴趣，那只需要知道 RoPE 位置编码有用即可!!
◆ 参考:
Transformer升级之路：2、博采众长的旋转式位置编码
Transformer升级之路：10、RoPE是一种β进制编码
Meta 最新模型 LLaMA RoPE 细节与代码详解
Rotary Trnasformer Github