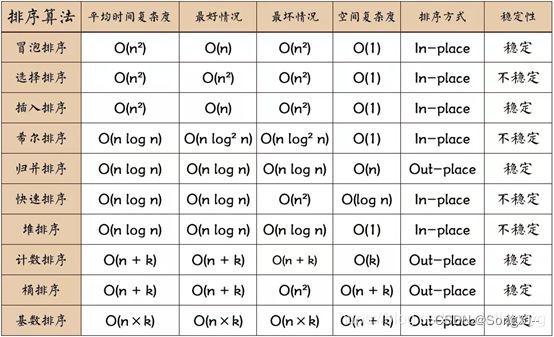
算法分析与设计：10 大排序算法大汇总（Java）

冒泡排序

• 相邻比较并交换位置，将大的数冒泡交换到最后。

    /*******************************************************************************
     * 冒泡排序（Bubble Sort）
     它重复地走访过要排序的元素，依次比较相邻两个元素，如果它们的顺序错误就把他们
     调换过来，直到没有元素再需要交换，排序完成。
     ********************************************************************************/
    public static int[] BubbleSort(int[] arr) {
        for (int i = 0; i < arr.length - 1; i++) {
            for (int j = 0; j < arr.length - 1 - i; j++) {
                if (arr[j] > arr[j + 1]) {
                    int temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                }
            }
        }
        return arr;
    }

时间复杂度：

• 最坏情况下为$O(N^2)$，此时待排序列为逆序，或者说接近逆序
• 最好情况下为$O(N)$，此时待排序列为升序，或者说接近升序。

空间复杂度：$O(1)$

插入排序

• 遍历每一个数，并将数字插入到合适的位置。

    /*******************************************************************************
     * 插入排序（Insertion Sort）
     将一个记录插入到已经排好序的有序表中。
     ********************************************************************************/
    public static int[] InsertionSort(int[] arr) {
        for (int i = 0; i < arr.length - 1; i++) {
            int current = arr[i + 1]; // 待归位的数
            int preIndex = i;         // 待归位的前面的一个数
            // 利用逐个比较的方式将待归位的数归位。
            while (preIndex >= 0 && current < arr[preIndex]) {
                arr[preIndex + 1] = arr[preIndex];
                preIndex--;
            }
            arr[preIndex + 1] = current; // 找到了正确的位置，进行归位
        }
        return arr;
    }

时间复杂度：

• 最坏情况下为$O(N^2)$，此时待排序列为逆序，或者说接近逆序
• 最好情况下为$O(N)$，此时待排序列为升序，或者说接近升序。

空间复杂度：$O(1)$

选择排序

• 每次从数组中选一个最小的放在开头。

    /*******************************************************************************
     * 选择排序（Selection Sort）
     第一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，
     然后再从剩余的未排序元素中寻找到最小（大）元素，然后放到已排序的序列的末尾。
     ********************************************************************************/
    public static int[] SelectionSort(int[] arr) {
        for (int i = 0; i < arr.length; i++) {
            int minIndex = i;
            for (int j = i; j < arr.length; j++) {
                if (arr[j] < arr[minIndex]) //找到最小的数
                    minIndex = j;           //将最小数的索引保存
            }
            int temp = arr[minIndex];
            arr[minIndex] = arr[i];
            arr[i] = temp;
        }
        return arr;
    }

时间复杂度：$O(N^2)$

空间复杂度：$O(1)$

希尔排序

    /*******************************************************************************
     * 希尔排序（Shell Sort）
     先选定一个小于N的整数gap作为第一增量，然后将所有距离为gap的元素分在同一组，
     并对每一组的元素进行直接插入排序。然后再取一个比第一增量小的整数作为第二增量，重复上述操作……
     ********************************************************************************/
    public static int[] ShellSort(int[] arr) {
        // step:步长
        for (int step = arr.length / 2; step > 0; step /= 2) {
            // 对一个步长区间进行比较 [step,arr.length)
            for (int i = step; i < arr.length; i++) {
                int value = arr[i];
                int j;
                // 对步长区间中具体的元素进行比较
                for (j = i - step; j >= 0 && arr[j] > value; j -= step) {
                    // j为左区间的取值，j+step为右区间与左区间的对应值。
                    arr[j + step] = arr[j];
                }
                // 此时step为一个负数，[j + step]为左区间上的初始交换值
                arr[j + step] = value;
            }
        }
        return arr;
    }

时间复杂度平均：$O(N^{1.3})$

空间复杂度：$O(1)$

快速排序

    /*******************************************************************************
     * 快速排序（Quick Sort）
     1.选择基准值：在待排序列中，按照某种方式挑出一个元素，作为基准值。
     2.分割操作：以该基准值在序列中的实际位置，把序列分成两个子序列，一边是比它大的值，另外一边是比它小的值。
     3.递归：对两个子序列进行快排，直到序列为空或者只有一个元素。
     ********************************************************************************/
    public static void QuickSort(int[] arr, int low, int high) {
        int p, i, j, temp;
        if (low >= high) {
            return;
        }

        p = arr[low];   // p是基准数，这里就是每个数组的第一个
        i = low;
        j = high;
        while (i < j) {
            // 右边当发现小于p的值时停止循环
            while (arr[j] >= p && i < j) {
                j--;
            }
            // 左边当发现大于p的值时停止循环
            while (arr[i] <= p && i < j) {
                i++;
            }
            temp = arr[j];
            arr[j] = arr[i];
            arr[i] = temp;
        }
        arr[low] = arr[i];
        arr[i] = p;
        QuickSort(arr, low, j - 1);  // 对左边快排
        QuickSort(arr, j + 1, high); // 对右边快排
    }

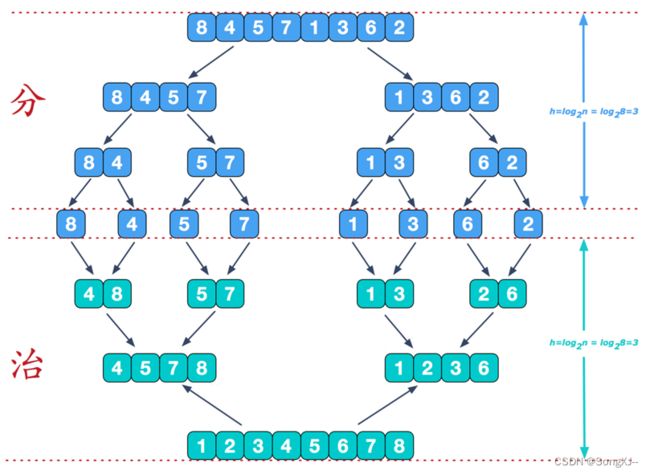
归并排序

1. 把长度为n的输入序列分成两个长度为n/2的子序列；
2. 对这两个子序列分别采用归并排序；
3. 将两个排序好的子序列合并成一个最终的排序序列。

    /*******************************************************************************
     * 归并排序（Merge Sort）
     1.把长度为n的输入序列分成两个长度为n/2的子序列；
     2.对这两个子序列分别采用归并排序；
     3.将两个排序好的子序列合并成一个最终的排序序列。
     ********************************************************************************/
    public static void MergeSort(int[] arr, int low, int high) {
        int mid = (low + high) / 2;
        if (low < high) {
            // 递归地对左右两边进行排序
            MergeSort(arr, low, mid);
            MergeSort(arr, mid + 1, high);
            // 合并
            merge(arr, low, mid, high);
        }
    }
    public static void merge(int[] arr, int low, int mid, int high) {
        int[] temp = new int[high - low + 1];   // temp数组用于暂存合并的结果
        int i = low;    // 左半边的指针
        int j = mid + 1;   // 右半边的指针
        int k = 0;  // 合并后数组的指针
        // 将记录由小到大地放进temp数组
        for (; i <= mid && j <= high; k++) {
            if (arr[i] < arr[j])
                temp[k] = arr[i++];
            else
                temp[k] = arr[j++];
        }
        // 接下来两个while循环是为了将剩余的放到temp数组中
        while (i <= mid)
            temp[k++] = arr[i++];
        while (j <= high)
            temp[k++] = arr[j++];

        // 将temp数组中的元素写入到待排数组中
        for (int l = 0; l < temp.length; l++)
            arr[low + l] = temp[l];
    }

时间复杂度：

• 最佳情况，$O(n)$
• 最差情况，$O(nlogn)$
• 平均情况，$O(nlogn)$

空间复杂度 $O(N+logN)$

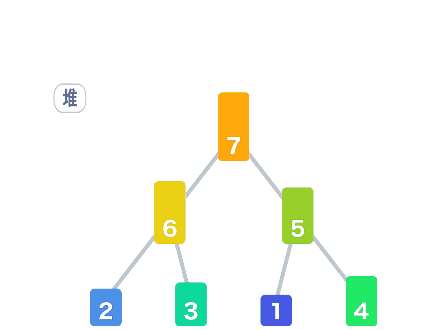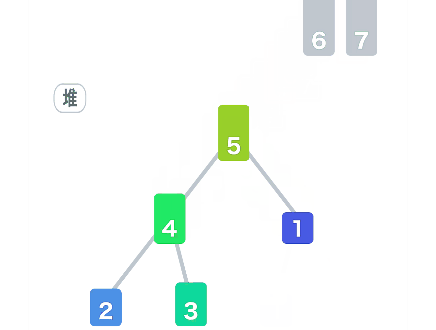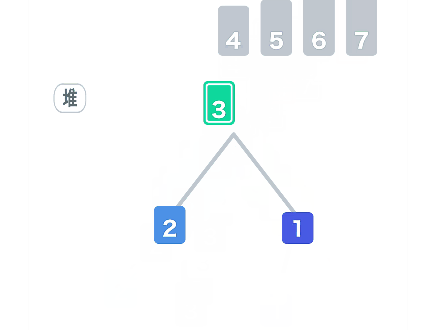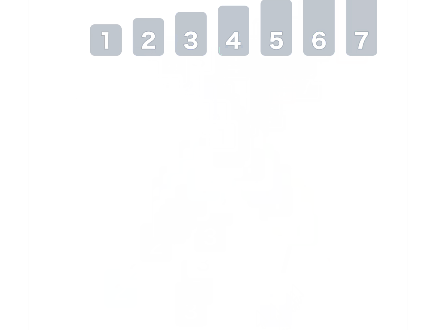
堆排序

通过完全二叉树构建大顶堆，并维护大顶堆的性质。

    /*******************************************************************************
     * 堆排序（Heap Sort）
     通过完全二叉树构建大顶堆，并维护大顶堆的性质。
     ********************************************************************************/
    public static void HeapSort(int[] arr) {
        // 构建一个大顶堆
        for (int i = arr.length / 2 - 1; i >= 0; i--) { // 从倒数第一个非叶子节点开始
            adjustHeap(arr, i, arr.length - 1);// 从第一个非叶子节点从下至上，从左至右调整结构
        }
        for (int i = arr.length - 1; i >= 0; i--) {
            // 将堆顶元素与末尾元素交换 将最大元素沉到数组末尾 + 重新调整堆结构
            int temp = arr[0];
            arr[0] = arr[i];
            arr[i] = temp;
            adjustHeap(arr, 0, i); // 将a中前i个记录重新调整为大顶堆
        }
    }


    public static void adjustHeap(int[] array, int index, int length) {
        int temp = array[index]; // 取出当前元素
        // i节点是index节点的左子节点
        for (int i = 2 * index + 1; i < length; i = 2 * i + 1) {
            if (i + 1 < length && array[i] < array[i + 1]) i++;    // 表明左子节点小于右子节点，将指针移至较大节点

            if (array[i] > temp) {  // 如果子节点大于父节点
                array[index] = array[i];    // 将较大值赋给当前节点
                index = i;  // 指针移向子节点
            } else break;
        }
        // 循环结束，已经将最大值放在了堆顶，将temp值放到最终的位置
        array[index] = temp;
    }

时间复杂度：$O(nlogn)$。（由于堆排序对原始记录的状
态并不敏感，因此它无论是最好、最坏和平均时间复杂度均为$O(nlogn)$。）

空间复杂度：$O(1)$

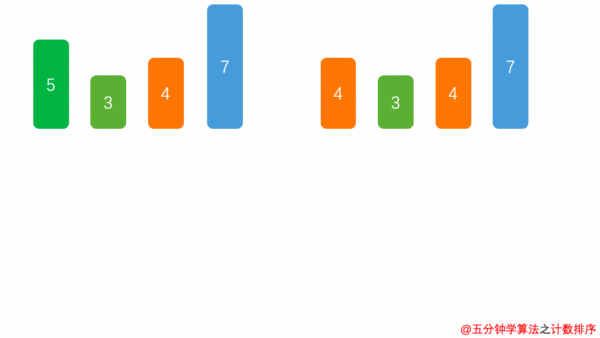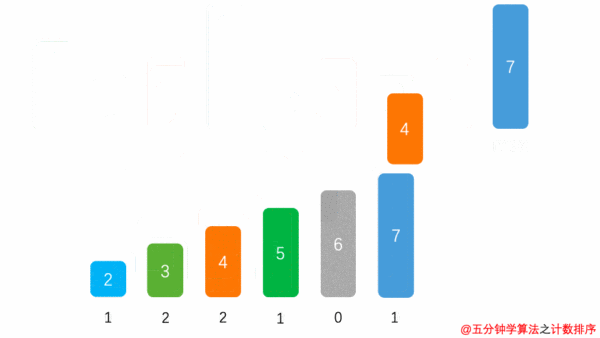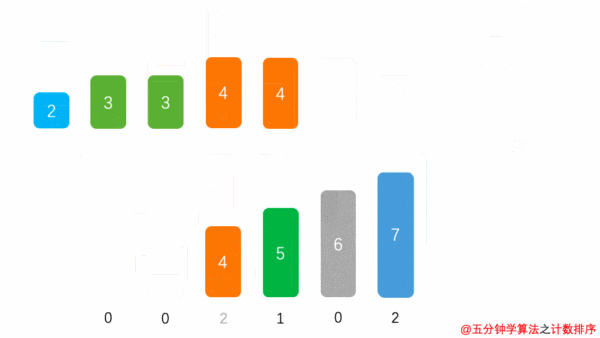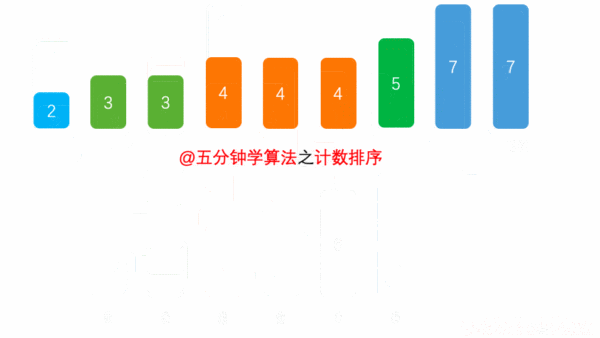
计数排序

找出待排序的数组array中最大的元素max
统计数组中每个值为 i 的元素出现的次数，存入数组 count 的第 i 项
对所有的计数累加（从 count中的第一个元素开始，每一项和前一项相加）
反向填充目标数组：将每个元素 i 放在新数组的第 count [i] 项，每放一个元素就将 count [i] 减去

    /*******************************************************************************
     * 计数排序（Count Sort）
     1.开辟一个长度为 maxValue-minValue+1 的数组。
     2.分配。扫描一遍原始数组，以当前值- minValue 作为下标，将该下标的计数器增1。
     3.收集。扫描一遍计数器数组，按倒序把值收集起来。
     ********************************************************************************/
    public static void CountSort(int[] arr) {
        // 得到数组的最大值和最小值，并推算出差值d
        int max = arr[0];
        int min = arr[0];
        for (int i = 1; i < arr.length; i++) {
            if (arr[i] > max) max = arr[i];
            if (arr[i] < min) min = arr[i];
        }
        int d = max - min;
        // 创建统计数组并统计对应的元素个数
        int[] countArray = new int[d + 1];
        for (int j : arr)
            countArray[j - min]++;
        // 统计数组做变形，后边的元素等于前面的元素之和
        for (int i = 1; i < countArray.length; i++)
            countArray[i] += countArray[i - 1];
        // 倒序遍历原始数组，从统计数组中找到正确的位置，输出到结果数组
        int[] sortedArray = new int[arr.length];
        for (int i = arr.length - 1; i >= 0; i--) {
            sortedArray[countArray[arr[i] - min] - 1] = arr[i]; // 给sortedArray的当前位置赋值
            countArray[arr[i] - min]--; // 给countArray的位置的值--
        }
        // 将temp数组中的元素写入到待排数组中
        System.arraycopy(sortedArray, 0, arr, 0, sortedArray.length);
    }

时间复杂度：

• 最佳情况，$O(n+k)$
• 最差情况，$O(n+k)$
• 平均情况，$O(n+n)$

空间复杂度 $O(k)$

桶排序

桶排序可以看成是计数排序的升级版，它将要排的数据分到多个有序的桶里，每个桶里的数据再单独排序，再把每个桶的数据依次取出，即可完成排序。
桶排序：将值为i的元素放入i号桶，最后依次把桶里的元素倒出来。

    /*******************************************************************************
     * 桶排序（Bucket Sort）
     1.设置一个定量的数组当作空桶子。
     2.寻访序列，并且把项目一个一个放到对应的桶子去。
     3.对每个不是空的桶子进行排序。
     4.从不是空的桶子里把项目再放回原来的序列中。
     ********************************************************************************/
    public static void BucketSort(int[] arr) {
        int max = arr[0];
        int min = arr[0];
        for (int i = 1; i < arr.length; i++) {
            if (arr[i] > max) max = arr[i];
            else if (arr[i] < min) min = arr[i];
        }
        // 最大值和最小值的差
        int diff = max - min;
        // 桶列表
        ArrayList<ArrayList<Integer>> bucketList = new ArrayList<>();
        for (int i = 0; i < arr.length; i++) {
            bucketList.add(new ArrayList<>());
        }
        // 每个桶的存数区间
        float section = (float) diff / (float) (arr.length - 1);
        // 数据入桶
        for (int j : arr) {
            //当前数除以区间得出存放桶的位置 减1后得出桶的下标
            int num = (int) (j / section) - 1;
            if (num < 0) num = 0;
            bucketList.get(num).add(j);
        }
        // 桶内排序
        for (ArrayList<Integer> integers : bucketList) {
            Collections.sort(integers);
        }
        // 写入原数组
        int index = 0;
        for (ArrayList<Integer> arrayList : bucketList) {
            for (int value : arrayList) {
                arr[index] = value;
                index++;
            }
        }
    }

时间复杂度：

• 最佳情况，$O(n+k)$
• 最差情况，$O(n^2)$
• 平均情况，$O(n+k)$

空间复杂度 $O(n+k)$

基数排序

将整数按每个位数分别比较，利用了桶的思想。

    /*******************************************************************************
     * 基数排序（Raix Sort）
     * 将整数按每个位数分别比较，利用了桶的思想。
     ********************************************************************************/
    public static void RaixSort(int[] arr) {
        // 得到数组中最大的数
        int max = arr[0];
        for (int i = 1; i < arr.length; i++)
            if (arr[i] > max) max = arr[i];
        // 得到最大数是几位数，通过拼接一个空串将其变为字符串进而求得字符串的长度，即为位数
        int maxLength = (max + "").length();
        // 定义一个二维数组，模拟桶，每个桶就是一个一维数组，为了防止放入数据的时候桶溢出，将桶的容量设置得大一些
        int[][] bucket = new int[10][arr.length];
        // 记录每个桶中实际存放的元素个数
        int[] bucketElementCounts = new int[10];
        // 通过变量n帮助取出元素位数上的数
        for (int i = 0, n = 1; i < maxLength; i++, n *= 10) {
            for (int value : arr) {
                int digitOfElement = value / n % 10;    // 针对每个元素的位数进行处理
                bucket[digitOfElement][bucketElementCounts[digitOfElement]] = value;    // 将元素放入对应的桶中
                bucketElementCounts[digitOfElement]++;    // 将桶中的元素个数++
            }
            // 按照桶的顺序取出数据并放回原数组
            int index = 0;
            for (int k = 0; k < bucket.length; k++) {
                if (bucketElementCounts[k] != 0) {    // 如果桶中有数据，才取出放回原数组
                    for (int l = 0; l < bucketElementCounts[k]; l++) {    // 说明桶中有数据，对该桶进行遍历
                        arr[index++] = bucket[k][l];    // 取出元素放回原数组
                    }
                }
                bucketElementCounts[k] = 0;    // 每轮处理后，需要将每个bucketElementCounts[k]置0
            }
        }
    }

时间复杂度：

• 最佳情况，$O(n\times k)$
• 最差情况，$O(n\times k)$
• 平均情况，$O(n\times k)$

空间复杂度 $O(n+k)$

汇总

---

版权声明：本文部分参考CSDN博主「~wangweijun」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq_42453117/article/details/100036347

『 如有不足或错误欢迎评论指正 』