Leetcode_二叉树递归问题自我总结

不断完善中…嘿嘿 今天也要加油干啊！

递归三部曲：

1. 确定递归函数的参数和返回值
2. 确定终止条件
3. 确定单层递归的逻辑

100. 相同的树

class Solution {
    public boolean isSameTree(TreeNode p, TreeNode q) {
        if(p==null&&q==null)    return true;
        if(p==null||q==null)     return false;
        if(p.val!=q.val)    return false;
        return isSameTree(p.left,q.left)&&isSameTree(p.right,q.right);
    }
}

101. 对称二叉树

class Solution {
    public boolean isSymmetric(TreeNode root) {
        if(root==null)  return true;
        return judge(root.left,root.right); 

    }
    public boolean judge(TreeNode l,TreeNode r)
    {
        if(l==null&&r==null)    return true;
        if(l==null||r==null)    return false;
        return (l.val==r.val)&&judge(l.left,r.right)&&judge(l.right,r.left);
    }
}

104. 二叉树的最大深度

class Solution {
    public int maxDepth(TreeNode root) {
        if(root==null)  return 0;
        return Math.max(maxDepth(root.left),maxDepth(root.right))+1;
    }
}

98.验证二叉搜索树

这里需要注意的是 需要借助辅助函数 因为单纯的递归并不能判断是否是二叉搜索树，比如

boolean isValidBST(TreeNode root) {
    if (root == null) return true;
    if (root.left != null && root.val <= root.left.val) return false;
    if (root.right != null && root.val >= root.right.val) return false;

    return isValidBST(root.left)&& isValidBST(root.right);
}

这只能判断左<根<右 并不能保证左子树都小于根都小于右子树，比如下面这个图就会被误判成BST

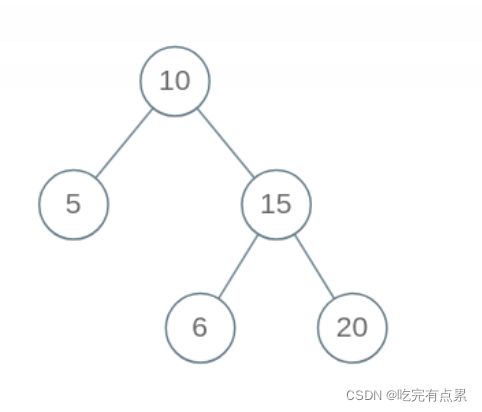
所以为了满足左子树小于根 右子树大于根
即满足如下条件，即需要设置上下界 而如果采用Integer的最值 ，leetcode会超过表示范围的极大数卡你，故采用Long

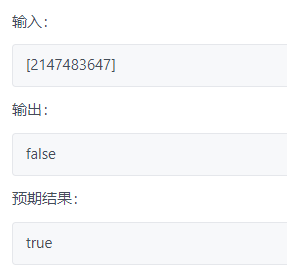
isValidBST(node.left, min, node.val) && isValidBST(node.right, node.val, max);

class Solution {
    public boolean isValidBST(TreeNode root) {
        return isValidBST(root, Long.MIN_VALUE, Long.MAX_VALUE);//递归入口
    }
    //overload
    public boolean isValidBST(TreeNode node, long min, long max) {

        if (node == null)   return true;
        if (node.val <= min || node.val >= max)     return false;
        //要保证左子树小于根 即左子树范围要在min与node之间 同样右子树范围在node与max上界之间
        return isValidBST(node.left, min, node.val) && isValidBST(node.right, node.val, max);
    }
}

700. 二叉搜索树中的搜索

class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        if(root==null||root.val==val)   return root;
        return root.val>val? searchBST(root.left,val):searchBST(root.right,val);
    }
}

701. 二叉搜索树中的插入操作

如果 root.val 大于目标值，说明目标值应当插入 root 的左子树中，问题变为了在 root.left 中插入目标值，递归调用当前函数；
如果 root.val 小于目标值，说明目标值应当插入 root 的右子树中，问题变为了在 root.right 中插入目标值，递归调用当前函数。

class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        //if(root==null)
        if(root==null)   return new TreeNode(val);
        if (root.val<val) 
            root.right= insertIntoBST(root.right,val);
        if(root.val>val)
            root.left= insertIntoBST(root.left,val);
        return root;
    }
}

450. 删除二叉搜索树中的节点

class Solution{

TreeNode deleteNode(TreeNode root, int key) {
    if (root == null) return null;
    if (root.val == key) 
    {
        //if(root.left==null&&root.right==null) return null----->以下语句包含了这个情况
        // 左空右不空，删除后右节点补上作为根结点 右空左不空同理
        if (root.left == null) return root.right;
        if (root.right == null) return root.left;
        //如果有左右孩子，就要考虑删除后 找左子树中最大的 或右子树中最小的接替自己
        //这里考虑取右子树最小的
        TreeNode minNode = getMin(root.right);
        root.val = minNode.val;
        root.right = deleteNode(root.right, minNode.val);
    } 
    else if (root.val > key) 
        root.left = deleteNode(root.left, key);
    else if (root.val < key) 
        root.right = deleteNode(root.right, key);
    return root;
}

TreeNode getMin(TreeNode node) {
    // BST 最左边的就是最小的
    while (node.left != null) node = node.left;
    return node;
} 

}

404. 左叶子之和

class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        if(root==null)  return 0;//终止条件
        /* 单层递归逻辑*/
        int mid_sum=0;
        //左叶子的判定依靠父结点 即父结点存在左孩子且左孩子无左右孩子
        if(root.left!=null&&root.left.left==null&&root.left.right==null)
            mid_sum+=root.left.val;
        return mid_sum+sumOfLeftLeaves(root.left)+sumOfLeftLeaves(root.right);
    }
}