泰勒图(Taylor Diagrams)和常用模型评价指标小结
文章内容仅用于自己知识学习和分享,如有侵权,还请联系并删除 :)
(一)泰勒图
1. 原理
1.1 定义
泰勒图(Taylor diagram) 可以简单的理解为一种的可同时展示相关系数(their correlation)、中心均方根误差(their centered root-mean-square difference )、标准差(the amplitude of their variations , represented by their standard deviations) 三个指标的可视化图表 [1]。
在做模型相关的工作时,我们经常会需要比较模拟效果。当使用多个模型时,看那个模型的模拟效果更好些,模拟误差更小,仅仅画散点图进行比较是不直观的。Taylor Diagram 泰勒图是一种可以直观进行模型比较的方法。它巧妙利用三角函数几何原理,把三种评价模型的指标在一张图上展现 [4]。
1.2 我们为什么要用泰勒图验证模型模拟精度?
这里主要介绍为三个指标所代表的含义和为什么选择以上三个指标 [1][2]。
1) 相关系数(their correlation)
2) 中心均方根误差(their centered root-mean-square difference )
3) 标准差 (the amplitude of their variations , represented by their standard deviations)
4) 为什么选择这三个指标?
-
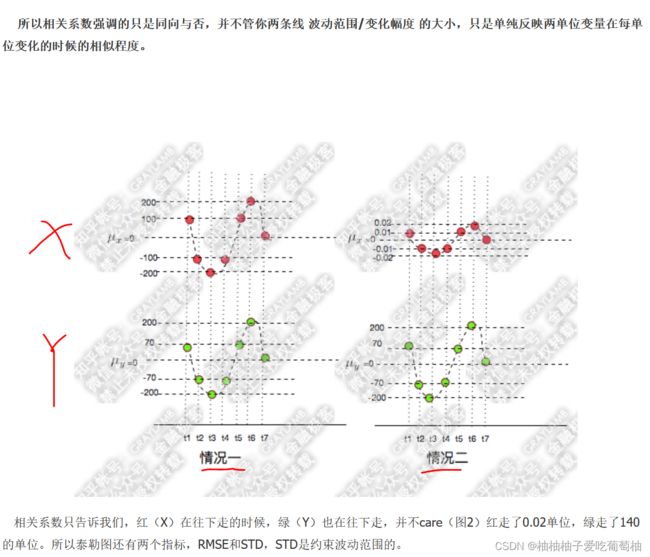
为了研究两个变量在变化过程中的相似程度,我们引入了相关系数。如下图可知,情况1和情况2中,X(红)和 Y(绿)的 同步率都很高,意味着情况1和情况2,X和Y的相关系数都很高。
-
但是在X、Y两个变量同向变化时候,X变化的幅度不一样。 这时候就需要引入中心均方根误差和标准差来描述变化的幅度。(详细描述可参考[1] link )
2. 案例解读
这里以评估GPP模型表现为例,介绍泰勒图的应用,具体描述可见 [2] link
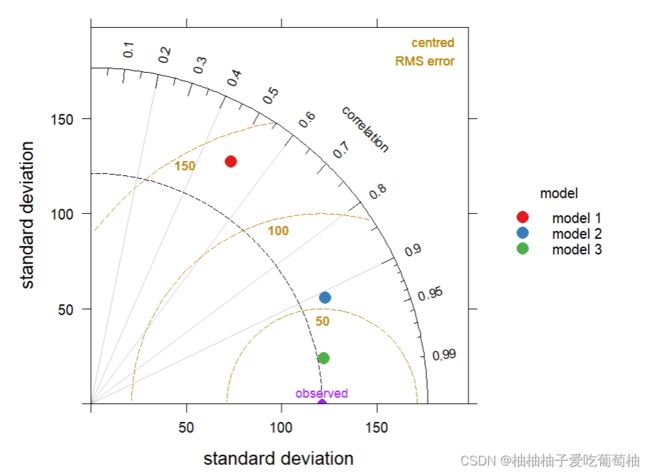
简单来说,泰勒图能够直观地展示下述的四种信息
- 模型值与真实值之间的相关系数(R)
- 模型值的标准差(std)
- 真实值的标准差(std)
- 模型值与真实值的中心均方根误差(RMSE)
(二)绘制方法
这里主要介绍基于R语言的绘制方法 [7]。
step1: 安装 package
# R-openair包是一个提供空气质量数据(air quality data)的第三方包,其提供的TaylorDiagram() 绘图函数就可以很好的绘制泰勒图
install.package("tidyverse")
install.package("openair")
step2: 示例代码
library(openair)
library(tidyverse)
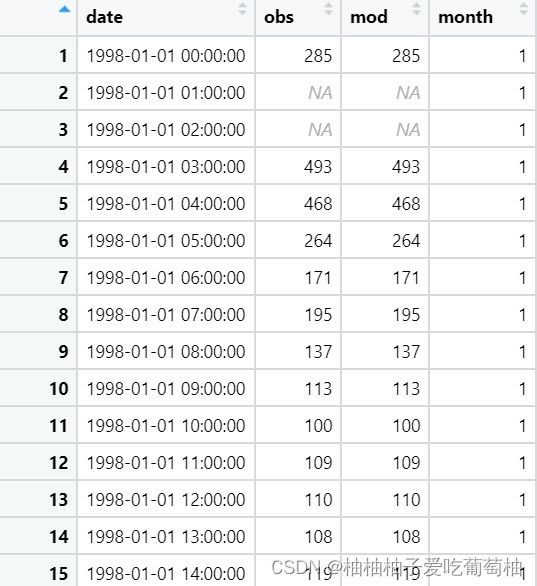
# Step2-1: 加载数据
dat <- selectByDate(mydata, year = 2003)
dat <- data.frame(date = mydata$date, obs = mydata$nox, mod = mydata$nox)
dat <- transform(dat, month = as.numeric(format(date, "%m")))
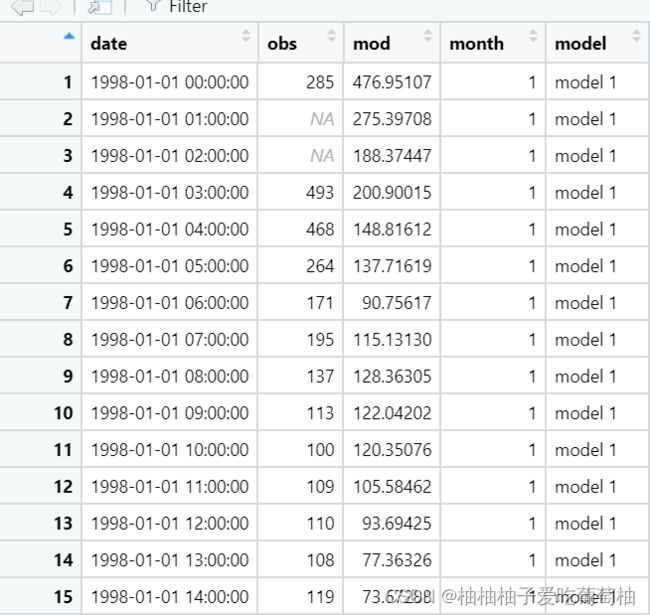
mod1 <- transform(dat, mod = mod + 10 * month + 10 * month * rnorm(nrow(dat)),
model = "model 1")
# model 1
mod1 <- transform(mod1, mod = c(mod[5:length(mod)], mod[(length(mod) - 3) :
length(mod)]))
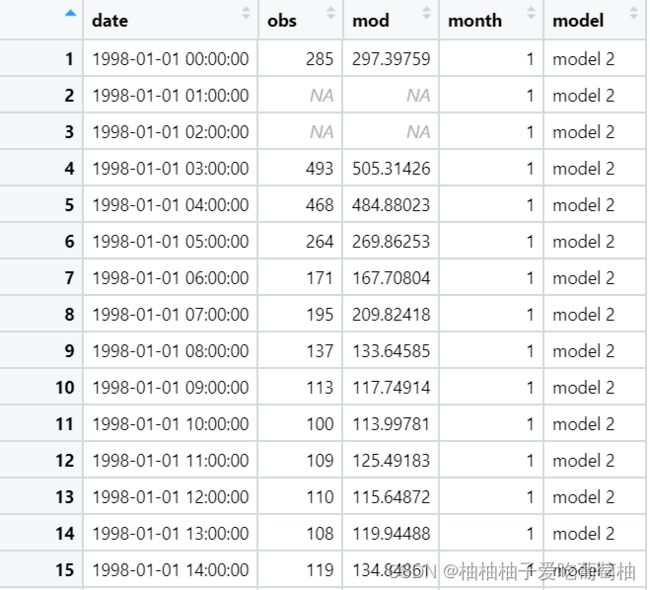
# model 2
mod2 <- transform(dat, mod = mod + 7 * month + 7 * month * rnorm(nrow(dat)),
model = "model 2")
# model 3
mod3 <- transform(dat, mod = mod + 3 * month + 3 * month * rnorm(nrow(dat)),
model = "model 3")
mod.dat <- rbind(mod1, mod2, mod3)
# Step2-2: 可视化绘制 (结果见下方)
## -----------------------------
## (1) basic Taylor plot
## -----------------------------
TaylorDiagram(mod.dat, obs = "obs", mod = "mod", group = "model")
## -----------------------------
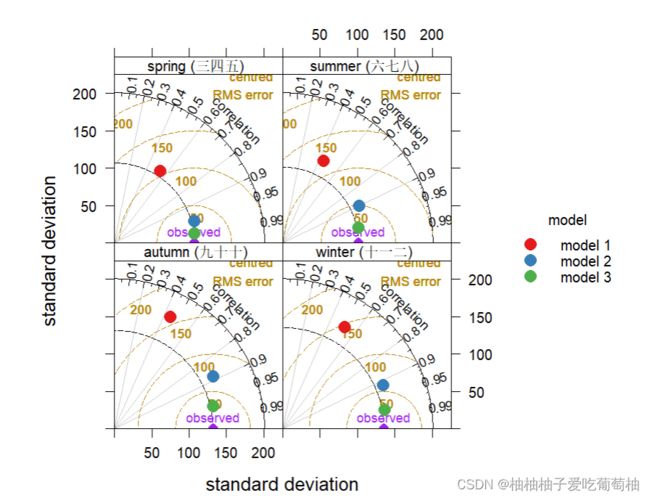
## (2) Taylor plot by season
## -----------------------------
TaylorDiagram(mod.dat, obs = "obs", mod = "mod", group = "model", type = "season")
## -----------------------------
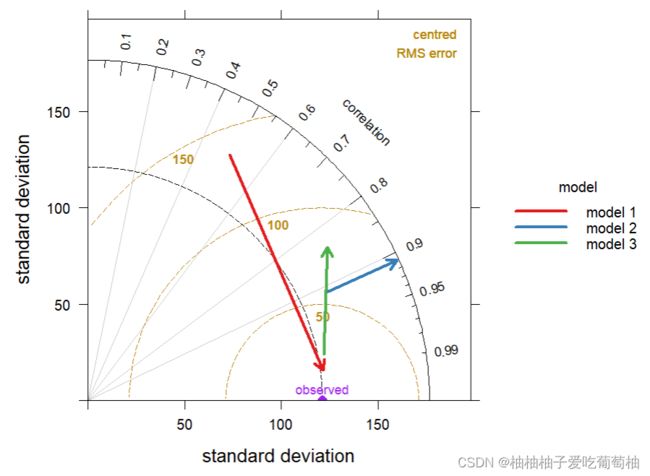
## (3) now show how to evaluate model improvement (or otherwise)
## -----------------------------
mod1a <- transform(dat, mod = mod + 2 * month + 2 * month * rnorm(nrow(dat)),
model = "model 1")
mod2a <- transform(mod2, mod = mod * 1.3)
mod3a <- transform(dat, mod = mod + 10 * month + 10 * month * rnorm(nrow(dat)),
model = "model 3")
mod.dat2 <- rbind(mod1a, mod2a, mod3a)
mod.dat$mod2 <- mod.dat2$mod
## now we have a data frame with 3 models, 1 set of observations
## and TWO sets of model predictions (mod and mod2)
## do for all models
TaylorDiagram(mod.dat, obs = "obs", mod = c("mod", "mod2"), group = "model")
## -----------------------------
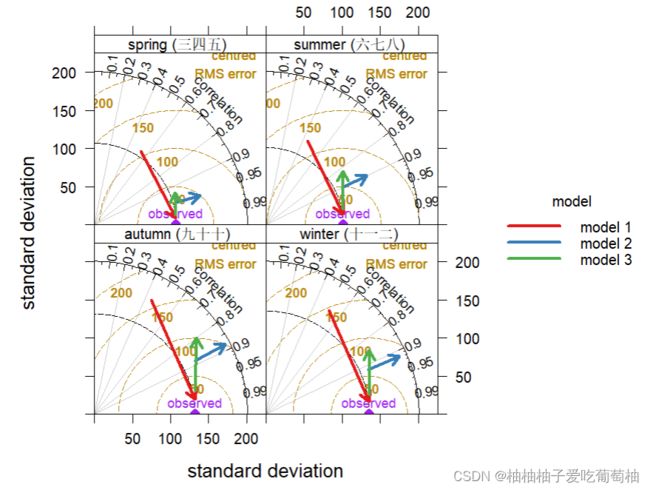
## (4) all models, by season
## -----------------------------
TaylorDiagram(mod.dat, obs = "obs", mod = c("mod", "mod2"), group = "model",
type = "season")
## -----------------------------
##(5) consider two groups (model/month). In this case all months are shown by model
## but are only differentiated by model.
## -----------------------------
TaylorDiagram(mod.dat, obs = "obs", mod = "mod", group = c("model", "month"))
step3: 输出变量展示
step4: 绘制生成的图
(2) Taylor plot by season
(3) now show how to evaluate model improvement (or otherwise)
(4) all models, by season
(5) consider two groups (model/month). In this case all months are shown by model but are only differentiated by model
(三)Reference
[1] 科学网: 我们为什么要用泰勒图验证模型模拟精度?: link (原理)
[2] 知乎: 带散点标注的泰勒图绘制(Taylor Diagram)——R语言: link (原理和案例)
[3] 知乎:泰勒图(Taylor Diagrams)原理及绘制 link
[4] 科学网:Use R: 画泰勒图 Taylor Diagram,模型比较一目了然: link (原理)
[5] CSDN: 泰勒图(Taylor diagram): link
[6] 超干货 | 泰勒图(Taylor diagram)绘制方法大汇总: link
[7] R package和案例:link