matlab电子双缝衍射,Matlab在《原子物理学》教学中的应用——以电子双缝衍射实验为例...
1. 引言
随着社会的发展、科技的更新,国家对培养创新型人才的重视程度不断提升,党的十九大报告提出“加快建设创新型国家”,人民日报发表“为新时代培养更多创新人才”社评。对高校教育工作者来说,有责任和义务为国家发现和培养创新型人才。如何在教学过程中培养大学生的创新思维是目前高校培养学生的一项重要任务。根据人才培养的需求,我们也积极开展创新型教学研究 [1] [2],在教学过程中引入先进教学方法,在传统知识范畴中有效挖掘创新元素,拓展学生知识面,培养学生的创新思维、创新能力和创新意识。
原子物理学是物理专业学生一门重要的核心基础课程,其属于近代物理理论范畴,是经典物理理论向量子力学过渡的桥梁 [3] [4]。这门课程包含了19到20世纪众多科学家的智慧的结晶,体现了他们在研究过程中的创新思维,特别适合作为培养物理专业学生创新思想和创新能力的载体。原子物理学是一门以实验为基础的课程,然而受条件限制,原子物理学课程并没有开设相应的实验课程,学生在学习过程中对实验相关现象只能停留在理论认识上,对实验现象的理解很模糊。Matlab程序中包括功能强大的库函数,具有界面可视化、操作简单等优点,已被国内外高校广泛应用到不同学科的计算机辅助教学中。我们也尝试使用Matlab辅助原子物理学课程的教学,通过引导学生对具体物理问题进行分析,根据理论结果设计程序,使用Matlab可视化界面展现实验结果,并对结果进行分析和比较,加深对物理问题的理解。这一方面可以形象地展示实验现象,另一方面培养学生创新能力和利用已有知识体系解决实际问题能力。本文中,我们以电子双缝衍射实验为例,介绍使用Matlab程序辅助原子物理学教学的具体思路。
2. 电子双缝衍射概率模型的构建
2.1. 德布罗意假设概率模型 [3] [4] [5]
质量为m的电子经电场加速后具有速度v,其对应的德布罗意波长为:
λ
=
h
p
=
h
m
v (1)
当
v
≪
c (c为光速)时,电子波的波长为:
λ
=
h
2
m
e
U (2)
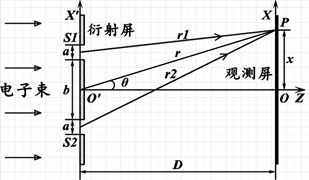
式(2)中U为加速电压。按照波动理论,电子穿过双缝将产生衍射现象,如图1所示。
电子的双缝衍射对应的强度分布函数为:
I
(
x
)
=
I
0
sin
2
(
π
a
λ
sin
θ
)
(
π
a
λ
sin
θ
)
2
cos
2
[
π
(
a
+
b
)
λ
sin
θ
] (3)
式(3)中a为缝宽,b为双缝间距,
θ 为衍射角,
I
0 为
x
=
0 处的衍射强度。当
x
≪
D 时(D为缝与屏的间距),有:
sin
θ
≈
tan
θ
=
x
D (4)
将式(4)代入式(3)中得到:
I
(
x
)
=
I
0
sin
2
(
π
a
λ
D
x
)
(
π
a
λ
D
x
)
2
cos
2
[
π
(
a
+
b
)
λ
D
x
] (5)
由式(5)知,衍射强度最大值在
x
=
0 处,且
I
max
=
I
0。则x处相对于
I
0 的相对衍射强度K为
K
=
I
(
x
)
I
0
=
sin
2
(
π
a
λ
D
x
)
(
π
a
λ
D
x
)
2
cos
2
[
π
(
a
+
b
)
λ
D
x
] (6)
显然
K
∈
[
0
,
1
]。
Figure 1. Experimental apparatus for electron double slit diffraction
图1. 电子双缝衍射实验装置
2.2. 量子力学概率模型 [3] [4] [5]
基于量子力学,微观实物粒子的波函数为:
Ψ
(
x
,
t
)
=
Ψ
0
e
i
ℏ
(
p
z
−
E
t
) (7)
由费曼路径积分理论,t时电子到达观测屏上P点的衍射波函数可以写为:
Ψ
(
x
,
t
)
=
2
Ψ
0
sin
(
k
a
2
sin
θ
)
k
a
2
sin
θ
cos
[
k
a
+
b
2
sin
θ
]
e
i
ℏ
(
p
z
−
E
t
) (8)
式中,
k
=
2
π
λ。电子经过双缝在观测屏上P点出现的概率密度分布情况为:
ω
(
x
)
=
|
Ψ
(
x
,
t
)
|
2
=
4
|
Ψ
0
|
2
sin
2
(
π
a
2
sin
θ
)
(
π
a
2
sin
θ
)
2
cos
2
[
k
(
a
+
b
)
2
sin
θ
] (9)
令
ω
0
=
|
Ψ
0
|
2,则
ω
(
x
)
=
ω
0
sin
2
(
π
a
λ
sin
θ
)
(
π
a
λ
sin
θ
)
2
cos
2
[
π
(
a
+
b
)
λ
sin
θ
] (10)
设
D
≫
(
a
+
b
),则有
sin
θ
=
x
D (11)
将式(9)代入式(8)中,则
ω
(
x
)
=
ω
0
sin
2
(
π
a
λ
D
x
)
(
π
a
λ
D
x
)
2
cos
2
[
π
(
a
+
b
)
λ
D
x
]
=
ω
0
sin
2
(
A
x
)
(
A
x
)
2
cos
2
(
B
x
) (12)
其中,
A
=
π
a
λ
D,
B
=
π
(
a
+
b
)
λ
D。
将式(12)与式(6)比较,可以看出从德布罗意假设出发和从量子力学理论出发推导所得到的电子经过双缝在观测屏上P点出现的概率密度形式一致。
3. Matlab计算结果与分析
3.1. 电子双缝衍射实验程序设计
根据2.1和2.2中对电子通过双缝在观察屏上P点出现的概率密度函数,使用Matlab程序对电子双缝衍射实验现象进行模拟。
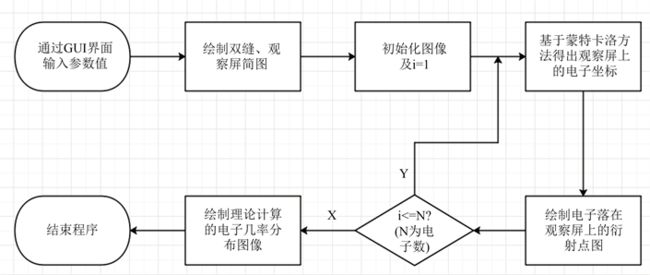
电子双缝衍射实验的程序主要包括参数的设置、数据和界面的初始化(h = 6.062559e−34; m = 9.10908e−31; q = 1.6021e−19)、实验装置简图的绘制、及电子通过双缝打在观察屏上坐标的获取、衍射理论相对几率分布图的绘制以及整个GUI界面的开始、刷新、重置、退出等按钮命令的建立。图2为电子双缝衍射实验Matlab仿真的程序流程图。
3.2. 不同电子数目的衍射图案对比
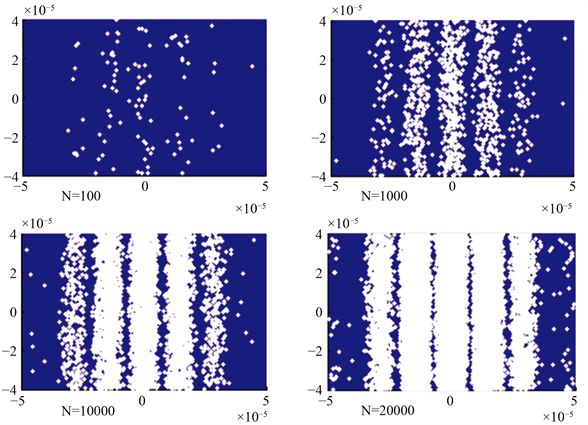
图3是当参数
a
=
0.16
μ
m
,
b
=
0.3
μ
m
,
D
=
0.25
m
,
U
=
2000
V,电子数目N分别为100、1000、5000、20,000时的电子衍射图像。通过模拟图像可以观察到当电子数目比较少(N = 100)时,电子打到屏幕上呈无规律性分布;而随着电子数目的逐渐增多(N = 1000、5000、20,000),电子的衍射特征越来越明显,电子在屏幕上的分布呈现出与光的杨氏双缝干涉实验相类似的规律,体现出电子的波动性。
Figure 2. Matlab simulation program flow chart of electron double slit diffraction
图2. 电子双缝衍射实验Matlab仿真程序流程图
Figure 3. Diffraction pattern for N = 100, 1000, 5000, 20,000
图3. 电子数目N = 100、1000、5000、20,000时的衍射图样
3.3. 缝宽及双缝间距对衍射图案的影响
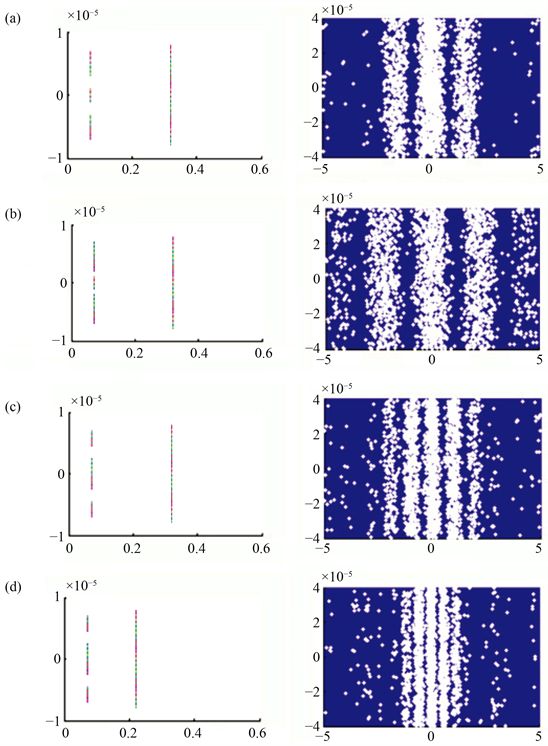
改变缝宽、双缝间距以及缝屏间距,观察衍射装置与衍射图样的变化。图4(a)和图4(b)是固定双缝间距为0.2 μm、缝屏间距为0.25 m,缝宽分别为0.2 μm和0.1 μm时的衍射图样;图4(c)和图4(d)是固定缝宽为0.2 μm、双缝间距为0.5 μm,缝屏间距分别为0.25 m和0.15 m时的衍射图样。从Matlab模拟图中可以看出:当其他条件固定不变时,电子衍射的双缝间距越大,衍射条纹越密;缝宽越大,衍射条纹越密;缝屏间距越大,衍射条纹越密。这一现象也与光的双缝干涉实验现象相吻合,体现了电子的波动特性。
Figure 4. (a) Diffraction pattern with crack width of 0.2 μm, double slit spacing of 0.2 μm and D of 0.25 m; (b) Diffraction pattern with crack width of 0.1 μm, double slit spacing of 0.2 μm and D of 0.25 m; (c) Diffraction pattern with crack width of 0.1 μm, double slit spacing of 0.5 μm and D of 0.25 m; (d) Diffraction pattern with crack width of 0.1 μm, double slit spacing of 0.2 μm and D of 0.15 m
图4. (a) 缝宽为0.2 μm、双缝间距为0.2 μm、D为0.25 m时的衍射图样;(b) 缝宽为0.1 μm、双缝间距为0.2 μm、D为0.25 m时的衍射图样;(c) 缝宽为0.1 μm、双缝间距为0.5 μm、D为0.25 m时的衍射图样;(d) 缝宽为0.2 μm、双缝间距为0.5 μm、D为0.15 m时的衍射图样
3.4. 衍射图像与几率分布函数图像的对比
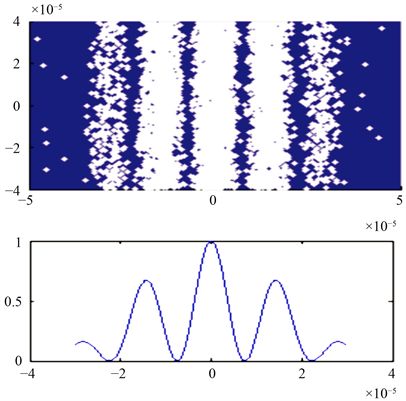
图5是电子双缝衍射实验图像与对应的衍射几率分布图像。对比两图可以看出电子双缝衍射图中的电子分布密度越大,对应的衍射几率越大;电子分布密度越小,对应的衍射几率也越小。由电子密度分布及衍射几率分布由屏幕中央向两侧呈由大到小的分布趋势,这也非常直观地体现出了电子的波动特性。
Figure 5. The diffraction probability density image corresponding to the electron double slit diffraction experimental image
图5. 电子双缝衍射实验图像相对应的衍射几率密度图像
通过3.1~3.4中模拟结果,可以看出电子落在空间中某处的密度大小代表着该处波的强度大小,电子双缝衍射实验体现了电子的粒子性,成功地证明了电子的波动性,这一实验结果恰巧佐证了波粒二象性的正确性。
3.5. 电子衍射图像与波函数
将电子衍射模拟图像与光学杨氏双缝干涉实验相比较,很容易理解物质波的波函数的物理意义。在杨氏双缝干涉实验中,在接收屏上明条纹对应的光波强度较大,光波振幅也比较大。反之,暗条纹对应的光波强度较小,光波振幅也比较小。用粒子的观点来理解光学杨氏双缝干涉实验产生的干涉条纹,明条纹对应的是光子出现概率较大的区域;反之,暗条纹对应的是光子出现概率较小的区域。将波动观点和粒子观点结合起来,即可以得出光子出现在观测屏上某处的概率与该处的光照强度(光波振幅大小的平方)成正比。将杨氏双缝实验中的结论推广到物质波中,就可以理解物质波波函数的物理意义:波函数模的平方对应于微观粒子在某处出现的概率密度。
4. 教学效果测评
我们使用Matlab软件对电子双缝衍射实验进行仿真模拟,并对实验现象和结果进行可视化处理,使得学生对实物粒子波动特性有了更清晰和更直观的认知,对实物粒子波粒二象性也有了更深刻的理解。另外,学生可以在教师的指导下,从模型构建到使用Matlab编程对电子双缝衍射实验进行仿真模拟,又可以培养学生学习主动性和解决问题的能力。在课后通过学生反馈,他们也普遍认为使用Matlab辅助教学,一方面可以加深对物理概念的理解,并提高他们的学习兴趣和积极性,另一方面还培养了他们在自主学习过程中发现问题、解决问题的能力以及创新能力。将Matlab辅助教学班(应用物理班2)期末成绩与上一届物理班(应用物理班1)进行比较也有了明显的提高,表1列出了了两个班级的期末考试统计信息。从表中可以看出,参加考试学生不及格人数有了大幅下降,平均分也有了显著的提高。从期末考试成绩也可以看出,使用Matlab软件辅助原子物理教学,不仅可以加深学生对物理概念的理解和对知识掌握的熟练度,还可以提高学生的学习兴趣,培养学生解决问题的能力及创新能力。
![]()
Table 1. Comparison of final grades of atomic physics courses
表1. 原子物理学课程期末成绩比较
5. 结论
本文中,我们以电子双缝衍射实验为例,分别德布罗意物质波假设和量子力学波函数出发,得到电子衍射实验中电子在屏幕上出现的几率一致。并使用Matlab对电子衍射实验现象进行模拟和分析,可以直观地观察到电子衍射实验现象类似于光的杨氏双缝干涉实验现象,有助于学生理解实物粒子的波粒二象性和波函数的物理意义。我们将Matlab引入到原子物理学的教学中,利用计算机模拟真实实验,可以直观地展示实验现象,帮助学生理解深奥的物理图像和物理概念,并有效地提高了学生的学习兴趣,培养学生的创新思维和创新能力。
基金项目
安徽理工大学校级重点教研项目(微信支持下大学物理翻转课堂教学研究和实践),安徽理工大学“三创融合”课程建设项目(将创新思维融入《原子物理学》课程教学改革的实践),安徽省质量工程示范实验实训中心项目(2017sxzx15),安徽省大学物理教学团队(2019jxtd046),安徽高校优秀人才项目(gxgwfx2019016)资助。