LeetCode-51.N皇后，Python的回溯法实现及详细讲解

51. N皇后

题目：

---

1. 思路

关于N皇后问题。它也是一个回溯问题。为何？因为它也符合类似”深度优先搜索“的树形思路。
例如，以4皇后为例，4*4的棋盘，假设我们从第一行开始算起，我们会发现，如果你选择第一行第一列(0, 0)，那么一次为出发点，你可以去尝试接下来第二行的所有位置(1, 0) ~ (1, 3)；假设你第二行选择了合适的放置位置(1, 2)，那么你可以接着以[(0,0), (1,2)]为出发点考虑第三行所有位置是否放置皇后合适。
显然，每个合适的皇后放置点，都是一个树形节点的开始，如下图所示：

0,0	0,1	0,2	0,3
1,0	1,1	1,2	1,3
2,0	2,1	2,2	2,3
3,0	3,1	3,2	3,3

                                            “ 我是棋盘。。。”

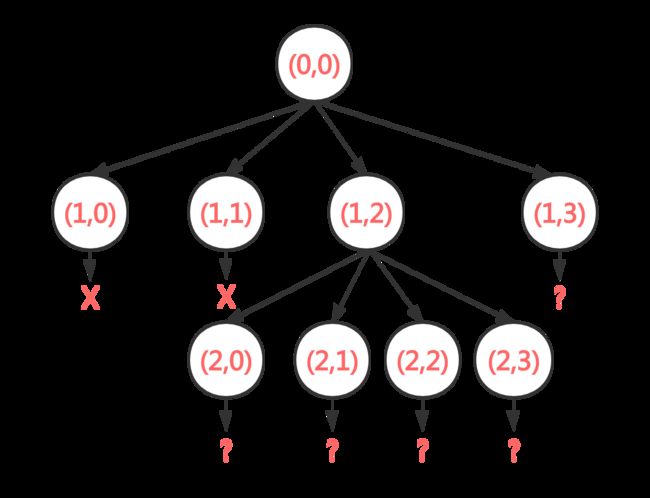
如图所示，这显然是个可以用递归处理的回溯思想/深度优先搜索思想解决的问题。所以提到回溯，我们的大框大概就架好了：

• 主函数用于开启递归、准备必要变量
• 递归函数，处理相同的递归步骤
• 若是有条件的递归，则再定义一个函数，判断是否可以进行递归

所以结合本题，思路大致梳理一下：

递归函数：

1. 从第一行开始，对所有位置(即col)进行for循环，判断此处是否可放Queen
   1.1 若可以放Queen，那么记录好当前Queen位置，进行下一行的递归判断(row+=1)
   1.2 若不能放Queen，不进入递归
2. 最后，不论是否可进入下一层递归，都要将col++.（原因：假设4皇后问题，前两行结果为[0, 2]，那么容易发现，第三行不论是哪个位置，都不能放置Queen，那么col++的循环会跳出，发生回溯，回到row没有步进的时候，将row=1那行的col=2进行步进，将前两行结果更新为[0, 3]。这就是即使is_valid()成立，col仍要步进的情况）
3. 当row == n（n是棋盘size）时，说明已经到了最后一行，完成了全部Queen的摆放，则要将当前的结果予以记录

主函数/入口函数：

1. 创建成员变量self.res=[], 用于存储递归过程中得到的结果。
2. 初始化一个列表tmp = [], 作用为在每一次递归过程中（即每一次深度优先搜索中，或者更具体地说，在树形思维中每一次走到n叉树的叶节点、走到无路可走or有答案的情况下），用于记录本次递归过程的结果。当然，根据上面递归函数所述，只有走到row==n时，才会被认为是一次正确放置N皇后的答案，才会将tmp记录到self.res里去。

递归条件判断函数：

1. 在知道当前所在的(row, col)棋盘位置的情况下，在已知此前rows的Queen摆放信息(tmp记录)的情况下，判断当前位置(row, col)是否可放置本行的Queen

2. 代码

class Solution:
    def solveNQueens(self, n: int) -> List[List[str]]:# 主函数，准备递归物料、递归函数入口
        self.res = []   # 答案记录器
        self.n = n      # 方便会用到的子函数
        tmp = [None for _ in range(self.n)]   # 递归复用数组，用一维数组记录Queen位置，数组的index就是row，index对应的元素就是col
        self.backtrace(tmp, row=0)
        return self.return_result()
        
    def backtrace(self, tmp, row):
        if row == self.n:  # 如果已经判断完全部的行了，就返回并记录吧
            self.res.append(tmp[:])   # 这里必须是tmp的切片，因为python切片是浅拷贝，浅拷贝的结果不会在后续递归中被修改掉
            return         # 这里必须有一个return，因为当row == self.n成立时，这条递归之路即该完美结束
        col = 0   # 每一行的循环判断，都从0位置开始
        while col < self.n:
            if self.is_valid(tmp, row, col):  # 判断当前位置是否可放Queen
                tmp[row] = col             # 若可以，则记录于tmp
                self.backtrace(tmp, row + 1)   # 然后开启下一行的递归判断(row+1)
            col += 1      # 不论是否成立，都应将col的位置步进(col+1)
        return  # 这里必须有一个return，因为当while循环跳出，说明本行所有col都不能放Queen，应发生回溯，目前的递归之路应提前结束
    
    def is_valid(self, tmp, row, col):
        for i, j in enumerate(tmp):
            # 在判断Queen是否可放置的时候，只有当前行之前的Queen值得被考虑。由于tmp是复用的，所以当前row及其之后的row都有可能已有无用记录
            if i == row:
                break
            if j == col or row - i == abs(col - j):  # 两个不可放Queen条件：1.在同列；2.在**左、右**两侧对角线。
                return False
        return True   # 全部经历过考验，则可以放置
    
    def return_result(self):   # 将结果转换成LeetCode要求的样子
        saver = []
        for arr in self.res:
            solve = []
            for pos in arr:
                line = ["."] * self.n
                line[pos] = "Q"
                solve.append(''.join(line))
            saver.append(solve)
        return saver

代码如上，思路很清晰，比我原本的分析只多了个LeetCode所需答案的生成函数 return_result()，但有些问题还是指的讨论的：

递归中 tmp 数组的复用

这也是我之前被卡壳的地方——那就是，在递归过程中，如何在每一次递归过程中都生成一个空list存放此次递归计算出的结果？或者说，code中所述的tmp数组，如何在每一次递归过程中复用？说实话，我觉得这应该算递归的普遍性问题，所以值得思考一下。
对于回溯问题，这种树形思维下的递归问题，最好的方法肯定是数组复用，因为树形的行走方式，注定数组一般而言是可以复用的。那么Python实现里如何复用，以及这么写为何可以复用就是个针对回溯的coding问题。
首先，若想复用数组，就当然是从递归入口处传入复用的数组。对于本题而言，数组长度就是棋盘size n。如code line-5，我们便建立了这样一个数组。因为在回溯的树形思维中，任何一条递归路走不通或走到底有结果的时候，我们都应将之终止，终止后会回到发生递归的地方(code line-17)，row相对于之前的递归回退一步。而tmp由于是复用的，所以会从row对应的index处开始重新更新，所以递归函数是这样复用数组的。
其次，对于结果的记录，如code line-11，我记录的是tmp的切片。因为若仅记录tmp，那么在后面复用的过程中，tmp一被改变，self.res中记录的tmp也会变化。而Python切片是浅拷贝，而self.res中没有可变对象，所以就隔离了后序递归中对tmp的修改。

---

最后，我们来聊聊递归

干货

• 当题干里出现”xxx所有组合“、”xxx所有解“的时候，我们应该想到回溯；
• 当你通过题干分析，分析出类似”深度优先搜索“的树形思路时，我们应该想到回溯

何谓“类似深度优先搜索的树形思路”？

以第LeetCode-17题为例，该题让写出2-9数字对应的字母所有组合。
随便举个例子——2，3，4。对于2，3，4，这三个数字各自分别对应3个字母，假设从数字2对应的a出发，到数字3，它又会有3条选择(d，e，f)，任选一个，到了4又是三个选择，情况如下：

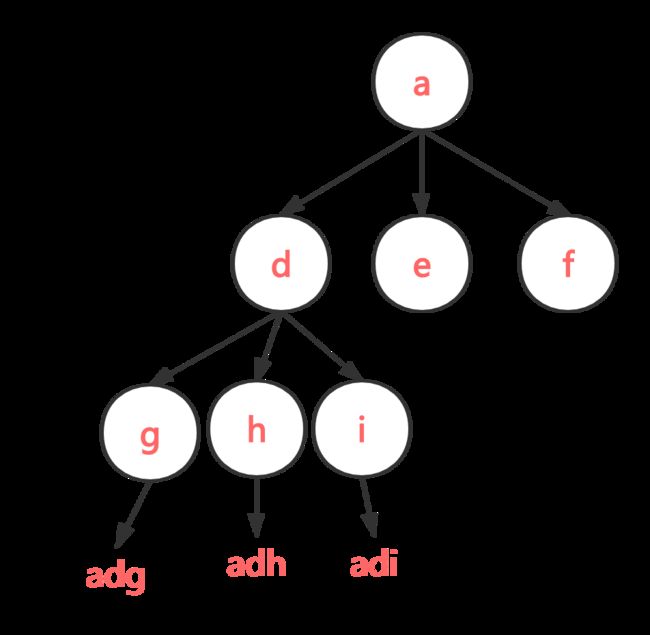
解决回溯问题的code捷径——递归！

回溯问题的通用代码框架

class Solution:
   def lcb(self, digits: str):
       self.res = []
       self.backtrace()
       return self.res
   
   def backtrace(self, ):
       if self.valid():
           return xxx or self.res.append(xxx)
       else:
           for i in arr:
               self.bc(i-1)
   def valid():
       return True

最后，附赠LeetCode-17的答案

class Miner:
    def lcb(self, digits: str):
        if not digits: 
            return []
        phone = {'2':['a','b','c'],
                 '3':['d','e','f'],
                 '4':['g','h','i'],
                 '5':['j','k','l'],
                 '6':['m','n','o'],
                 '7':['p','q','r','s'],
                 '8':['t','u','v'],
                 '9':['w','x','y','z']}
        str_list = [phone[d] for d in digits]
        self.res = []
        self.bc('', str_list)
        return self.res
        
    def bc(self, prefix, str_list):
        if not str_list:
            self.res.append(prefix)
        else:
            for j in str_list[0]:
                self.bc(prefix + j, str_list[1:])