论文阅读笔记:Attention: Self-Expression Is All You Need
论文阅读笔记:Attention: Self-Expression Is All You Need
- 摘要
- 简介
- 2 Transformer, Attention, Self-attention
-
- 2.1 Transformer
- 2.2 Attention
- 2.3 Self-attention
- 2.4 Masked attenion & Sparse attention
- 3 Kernel Regression, Non-local Means Denoising and Attention
-
- 3.1 Kernel regression
- 3.2 Non-local Means Denoising
- 4 Locally Linear Embedding (LLE) & Local Self-attention
-
- 4.1 LLE
- LLE VS Local-attention
- 5 Subspace clustering, Self-expression and Self-attention
- 5.1 Subspace clustering and Self-expression
-
- 5.2 使用不同正则化的自表达系数
- 5.3 Self-expressiveness VS Self-attention
- 6 结论
正在双盲审中的ICLR 2022论文,论文名字neta了著名的《Attention Is All You Need》,证明了Attention和各种聚类和去噪方法的内在联系
很有意思的文章,但也存在许多不足。这篇文章细致地回顾了各种Transformer模型的定义、直觉含义和进展(第2章),同时系统地与Self-Expression进行比较并给出了严格的证明(第3,4,5章三重比较),最后指明了可能的Attention和Self-Expression互相补充互相促进的可能性(attention的稀疏正则化和self-expression的过参数化、堆叠化)。不过本文没有做任何实验。
摘要
Transformer模型令人惊喜地同时在NLP和CV领域的各种学习任务中出色表现。Transformer的成功很大程度上归功于attention层的使用,该层通过注意力系数捕获数据token(如单词和图像块)之间的远程联系,注意力系数是全局的,并在测试时适应输入数据。在本文中,我们研究了注意力背后的原理及其与现有技术的联系。具体地说,我们证明了attention建立在流形学习和图像处理的历史长河之上,包括基于核的回归、非局部均值、局部线性嵌入、子空间聚类和稀疏编码等方法。值得注意的是,我们证明了self-attention与子空间聚类中的self-expression概念密切相关,self-expression将待聚类的数据点表示为所有其他点的线性组合,系数设计用于关注同一组中的其他点,从而捕获点之间的远程联系。我们还表明,可以使用有关稀疏编码和稀疏子空间聚类的现有文献,以更为原则的方式研究稀疏self-attention中的启发式算法。
简介
注意力这个单词本身,即有选择地专注于观察的某个子集,而忽略其他无关信息的能力,是人类感知的核心组成部分。例如,一个句子中只有几个单词可能对预测下一个单词有用,或者只有图像的一小部分可能与识别对象相关。
生物系统的这种特性激发了基于attention的神经架构的最新发展,如Transformer(2017年)、BERT(2018年)、GPT系列(2018-2019年)、RoBERTa(2019年)和T5(2019年),在各种NLP任务中取得了令人印象深刻的性能。基于attention的体系结构还延伸到了各种CV任务中,包括图像分类、目标检测和视觉问答等。
基于attention结构成功很大程度上归功于它们通过注意力系数捕获数据token之间的远程联系的能力,注意力系数是全局的、可学习的,并且在测试时适应新的输入。例如,NLP中的递归神经网络 (RNN) 结构使用有关前几个单词的信息预测句子中的下一个单词,而self-attention机制则基于所有单词之间的相互作用进行预测。类似地,计算机视觉中的卷积架构使用测试时不依赖于输入图像的权重计算图像块之间的局部交互,而视觉transformer能够计算全局交互。
在本文中,我们展示了attention背后的许多关键思想,我们在第2节中简要总结了这些思想,它们建立在流形学习和图像处理的长期历史基础之上。
-
在第3节中,我们展示了scaled dot product attention机制等同于使用高斯核的基于核的回归,正如最近指出的那样,通过选择其他核可以获得更一般的attention机制。我们还展示了非局部均值图像去噪算法,也可以理解为基于核的回归形式,这是视觉转换器(ViT)背后的主要构建块。我们认为,相对于基于核的回归,注意力的关键创新不在于它能够捕捉适应输入数据的全局联系(非局部手段已经做到了这一点),而在于使用许多可学习的超参数来定义注意力。相比之下,经典的内核方法通常只调整内核带宽。
-
在第4节中,我们建立了masked attention和局部线性嵌入(LLE)之间的联系。具体地说,我们证明了LLE使用masked attention机制学习数据集的低维表示,其中masks由数据点的最近邻定义。由此产生的系数不被限制为非负,因此允许正面和负面注意。此外,它们明确地依赖于多个数据token,而注意系数仅依赖于一对token。我们还表明,LLE的训练目标可以解释为一个填补空白的自监督学习目标。然而,LLE的一个关键限制是其局部邻域是预先指定的,因此数据点不能关注任何其他点。这个问题是通过self-expression来解决的,它将每个点连接到每个其他点,并使用稀疏正则化来显示需要关注的点。
-
在第5节中,我们发现self-attention与self-expression概念密切相关,其中待聚类的数据点表示为具有全局系数的其他点的线性组合,然后使用这种自表达系数来定义用于对数据进行聚类的数据关联矩阵。self-attention系数和self-expression系数之间的第一个区别是后者不一定是非负。第二个区别是,自表达系数并没有定义为具有可学习权重的参数化函数。相反,它使用无监督损失直接学习系数。第三个区别是,自表达系数通常被正则化为稀疏或低秩的。因此,我们认为,相比于自表达模型,self-attention的关键创新不在于其捕捉适应数据的全局联系的能力(因为self-expression已经做到了这一点),而是在于注意力机制并行地使用多个注意头,并堆叠到深层架构中。
我们总结了如何利用Self attention来提高Self expression能力的未来方向,反之亦然。例如,我们认为使用稀疏正则化自动选择最相关的系数,是处理大量数据token的一种更具原则性的方法;而不是像criss-cross attention(2019)那样将注意力限制在任意的局部近邻。这不仅可以通过对注意力系数使用稀疏正则化器来改进基于self-attention的体系结构,还可以通过使用self-attention来改进子空间聚类方法,正如最近在SENet, CVPR2021中提出的那样。这也允许通过堆叠多层自表达性将子空间聚类方法扩展到非线性流形。
2 Transformer, Attention, Self-attention
2.1 Transformer
transformer架构最初是为处理数据序列而设计的,例如,句子中的一系列单词。序列的每个元素首先通过适当的嵌入(如Word2vec)映射到向量空间。由于体系结构不依赖于输入序列的位置和顺序,因此在每个输入嵌入中都有额外的对位置的编码。之后输入的token由multi-head attention处理。该层将输出token看做输入标记的线性组合进行计算,输入token经由注意力系数加权,以捕获输入token之间的关联。然后,输出token由残差连接、层规范化(LN)、前馈网络(例如MLP)和对前馈网络的残差连接和层规范化处理。因此,transformer架构的主要组件是multi-head attention层。
2.2 Attention
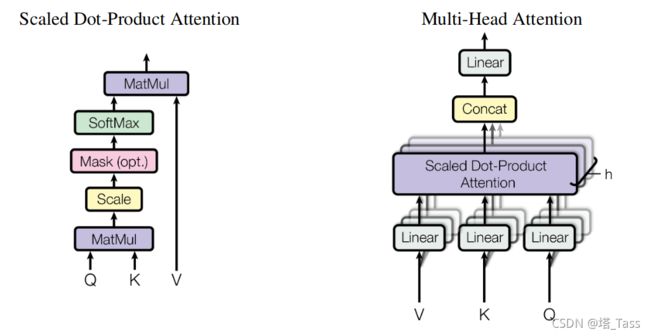
Attention层旨在捕获三种类型的输入token之间的交互信息:Query、Key和Value。它通过将Query与Key进行比较(Q和K矩阵乘法)来生成一组注意力系数,然后使用这些系数来生成Value的线性组合(注意力系数与V的矩阵乘法)。
经过Softmax处理后,对每个Query-Key点对,attention层计算注意力系数 c i j = c_{ij}= cij=attn ( k i , q j ) ∈ [ 0 , 1 ] (k_i,q_j)\in[0,1] (ki,qj)∈[0,1],并通过以下计算得到Value的线性组合:
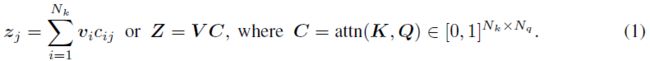
直观地说,注意系数 c i j c_{ij} cij度量了用当前Key去表示Query的重要程度,而表示 z i z_i zi线性组合了对Query最重要的Value。attention的计算机制有许多选择: 加性、乘性和点积。常用的选择是缩放点积,Query和Key按其维度的平方根缩放,然后将softmax用于Query和Key的点积,即:
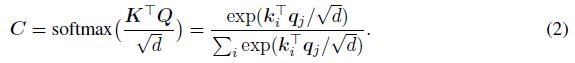
这样得到系数是非负的,且累和等于1,所以 z j z_j zj是这些Value的凸组合。让我们用简化的例子来说明注意力背后的直觉:
- NLP: 假设我们想把法语句子翻译成英语。设Query q j q_j qj为法语句子第j个单词的特征嵌入,设 k i = v i k_i=v_i ki=vi为英语对应句子第i个单词的特征嵌入。理想情况下, 注意力机制应确保仅针对正确的key-query翻译对 ( i , j ) (i,j) (i,j)的系数较大(即 c i j ≈ 1 c_{ij}≈ 1 cij≈1),那么在这种情况下,法语Query q j q_j qj的输出将是其到英语 z j = v i z_j=v_i zj=vi的翻译。
- CV: 假设给我们一个图像–标题对,我们想找出图像中的哪些区域对应于标题中的哪个单词。假设我们还有一组使用对象检测器从图像中提取的边界框。Query是标题中单词的word embedding,Key和Value是从边界框中提取的CNN特征。也就是说,注意机制是为了告诉我们每个单词要注意哪些区域。
当然,为了使多语言单词嵌入相互对齐,或者为了使单词的嵌入匹配图像特征,这两种特征都需要通过可学习的变换映射到公共潜在空间,这便是接下来的Self-attention。
2.3 Self-attention
设 X = [ x 1 , . . . , x N ] ∈ R D × N X=[x_1,...,x_N]∈\mathbb R^{D×N} X=[x1,...,xN]∈RD×N表示一组数据tokens,如单词或图像块。Self-attention的目标是捕捉这些tokens内部的交互信息。首先通过可学习的系数矩阵 W K , W Q , W V W_K,W_Q,W_V WK,WQ,WV将这些tokens转换为Key、Query和Value:
![]()
然后就可以像普通的attention一样学习到表示Z:
![]()
让我们用(Dosovitskiy et al.,2020)提出的Vision Transformer(ViT)来说明Self-attention背后的直觉。如图所示,ViT将输入图像划分为多个patchs的集合,并通过可学习的Linear Projection将这些patchs映射到一组向量。每个投影后的patch都添加了一个指示它在整个图像中位置的编码。由于ViT是为图像分类而设计的,因此在Transformer Encoder的输入中添加了一个额外的0号token用于捕获类信息和其他token一起学习。Transformer Encoder使用Self-attention处理所有这些token。

具体地说,新token为patch的线性组合,权重为patch之间关系的注意力系数。此外,将类token与patch tokens关联的注意力系数期望哪些patch需要注意,以对图像进行分类。然后,输出的类token通过MLP头得到类概率。使用交叉熵损失进行分类。
2.4 Masked attenion & Sparse attention
然而,softmax处理的使用通常会导致稠密的attention maps,其计算可能是内存和计算密集型的。此外,在文档摘要、问题回答或视觉基础等应用中,attention maps应是稀疏的。解决这一问题的一种方法是将非零注意系数限制在某些模式上,这是通过mask实现的,因此命名为masked attention。然而,预先定义的局部attention maps可能会错过重要的远程交互。作为替代方案,Martins&Astudillo提出用sparsemax算子替代softmax算子,这直接诱导稀疏的attention maps。然而不清楚为什么这样做会自动选择信息更丰富的token。这促使He等人提出了结合注意图的启发式方法。总的来说,在保持信息量最大的长程相互作用的同时诱导稀疏性的严格方法仍然是难以捉摸的。
3 Kernel Regression, Non-local Means Denoising and Attention
self-attention思想最早的体现之一即核回归。有趣的是,核回归也是著名的图像去噪算法的基础,即非局部均值(non-loacal means),我们认为该算法与Vision Transformer(ViT)密切相关。
3.1 Kernel regression
核回归是这样一种非参数方法的拟合函数 f : X → Y f:\mathcal X→\mathcal Y f:X→Y从 X × Y \mathcal X\times\mathcal Y X×Y中采样 ( x j , y j ) j = 1 N {(x_j,y_j)}^N_{j=1} (xj,yj)j=1N,它使用核密度估计器来近似最小均方误差预测器 f ^ ( x ) = E ( y ∣ x ) \hat f(\textbf x)=\mathbb E({\bf y|x}) f^(x)=E(y∣x)。具体来说,给定一个核 κ : X × X → R \mathcal κ:\mathcal X×\mathcal X→\mathbb R κ:X×X→R,人们可以将 f ^ ( x ) \hat f(\textbf x) f^(x)估计为 y j \textbf y_j yj值的加权组合:
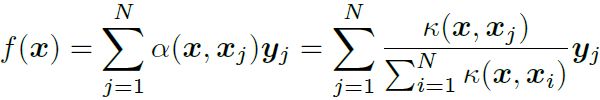
加权函数 α ( x , x j ) α(x,x_j) α(x,xj)编码了用 x j x_j xj预测 f ( x ) f(x) f(x)的相关性。当核 κ \mathcal κ κ是高斯核时,上式可化为:

因此,Nadayara-Watson回归是一种注意力机制,对于Query对应 q = x q=x q=x,Key对应 k j = x j k_j=x_j kj=xj,Value对应为 v j = y j v_j=y_j vj=yj,注意力函数为用于减去Query和Key之间的标准化平方距离的softmax。进一步假设Query和Key被规范化为 ∥ x ∥ 2 = ∥ x j ∥ 2 = 1 \| x\|_2=\| x_j\|_2=1 ∥x∥2=∥xj∥2=1使得 ∥ x − x j ∥ 2 2 = 2 ( 1 − x ⊤ x j ) \| x-x_j\|_2^2=2(1-x^\top x_j) ∥x−xj∥22=2(1−x⊤xj)提供缩放点积注意:
尽管有这种明显的联系,但高斯核的核回归是一种局部的注意力,无法捕捉一般的远程交互。这是因为的注意力权重取决于Key和Query之间的距离,而高斯核回归仅一个可调参数 σ σ σ:当σ非常小时,尽管计算了所有成对的交互,但大的交互只发生在局部邻域中;另一方面,当σ非常大时,所有权重就会变得相似,有 f ( x ) ≈ 1 N ∑ y j f(x)≈\frac {1}{N}\sum \textbf y_j f(x)≈N1∑yj,这显然不是有效的注意力。
可以说,相对于核回归,attention的关键优势在于为Key和Query加入了可学习的线性变换:若使 q = W x , k j = W x j q=Wx,k_j=Wx_j q=Wx,kj=Wxj,就得到了 q ⊤ k j = x ⊤ W ⊤ W x j q^\top k_j=x^\top W^\top Wx_j q⊤kj=x⊤W⊤Wxj。为了使核回归实现这样一种可学习的点积,它需要使用一个具有完全协方差矩阵 ∑ ∑ ∑的高斯核,并学习由 x ⊤ Σ − 1 x j x^\top Σ^{−1}x_j x⊤Σ−1xj给出的点积。
更一般地说,可以通过选择不同的核函数 κ κ κ来定义新的注意机制;另一方面,目前还不清楚是否所有现有的attention机制(例如,additive attention)都可以用核函数写出。
3.2 Non-local Means Denoising
图像去噪方法旨在去除图像中的噪声,最基本的是基于计算一组相邻像素的平均强度的去噪方法。通常,使用局部高斯加权平均值。例如,如果 x j x_j xj表示像素 j j j的2D坐标并且 y j y_j yj表示其强度或RGB值,则像素 x x x处的去噪图像采用核回归形式。因为σ通常较小(如3-11像素),高斯权重随距离 ∥ x − x j ∥ \| x-x_j\| ∥x−xj∥衰减非常快。在这种情况下,累和变成了高斯滤波器的卷积。因此,经典去噪是一种局部注意机制,Query和Key表示像素位置(即 q j = k j = x j q_j=k_j=x_j qj=kj=xj)而Value表示图像强度(即 v j = y j v_j=y_j vj=yj)。
Non-local Means对经典图像去噪进行了两个关键改进。首先,它计算所有像素强度的加权平均值,而不仅仅是 x x x的局部邻域。其次,它使用基于强度值 y j y_j yj而非像素位置 x j x_j xj的高斯核。这使得Non-local Means算法可以是非局部的,因为它可以找到其他(可能很远)具有类似强度的像素。具体地说,在其最简单的形式中,Non-local Means为:
因此,这种简化形式的非局部均值去噪是一种self-attention机制,具即 q j = k j = v j = y j q_j=k_j=v_j=y_j qj=kj=vj=yj。
Non-local Means算法的更一般的形式不是根据单个像素的强度 y y y和 y j y_j yj计算高斯核,而是根据分别以像素 x x x和 x j x_j xj为中心的patch的强度计算高斯核。这使得该算法能够处理相似的patch,因此对去噪非常有用。因此,非局部均值去噪是一种注意力机制,其中Query和Key是图像patch的强度,Value是中心像素的强度。Wang等人(2018年)注意到了这一联系,但Dosovitskiy等人(2020年)并未提及这一联系。事实上,Non-local Means的步骤相当于:
- 从图像中提取一组存在部分重叠的patches;
- 展平这些patches;
- 应用等价于注意力机制的非局部均值算法,其中Key和Query是展平后的patches,Value是其中心像素的强度。
因此,Non-local Means去噪与Vision Transformer密切相关,区别在于:
- 没有额外的分类token
- 对patch的投影为固定的而不是可学习的
- 没有向嵌入的patch添加位置编码
- 这是一种单头单层的self-attention机制,没有进行规范化或接一个fc层。
4 Locally Linear Embedding (LLE) & Local Self-attention
LLE通过使用mask的局部自注意力机制来学习数据集的低维表示。具体地说,本节证明了LLE的系数可以用最近邻定义的masks来解释为Local Self-attention权重。我们注意到,LLE系数不受非负约束因此允许正注意力和负注意力,并且LLE系数明确地依赖于多个数据token,这与仅依赖于一对token的加法注意力和缩放点积注意力不同。最后,本节证明了LLE的训练目标可以解释为一个填补空白的自监督学习目标。
4.1 LLE
LLE的目标是对给定数据集 { x j } j = 1 N ⊂ R D \{x_j\}^N_{j=1}\subset \mathbb R^D {xj}j=1N⊂RD学到一个局部线性的、低维表示的embedding { y j } j = 1 N ⊂ R d \{y_j\}^N_{j=1}\sub \mathbb R^d {yj}j=1N⊂Rd,LLE将每个数据点 x j x_j xj用它的K个最近邻的仿射组合进行表出来计算这种低维嵌入,即:找到一组系数 c i j ∈ R c_{ij}\in\mathbb R cij∈R使得 x j ≈ ∑ i ∈ N j x j c i j x_j≈\sum_{i\in N_j}x_jc_{ij} xj≈∑i∈Njxjcij且 ∑ i ∈ N j c i j = 1 \sum_{i\in N_j}c_{ij}=1 ∑i∈Njcij=1( N j ⊂ { 1 , . . . , N } N_j\sub \{1,...,N\} Nj⊂{1,...,N}为 x j x_j xj的K近邻集合)。 c i j c_{ij} cij是通过最小化如下重构损失来得到的:
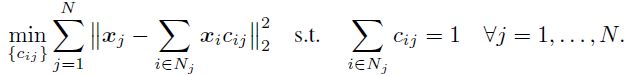
一旦找到这些系数,LLE就会找到以原点为中心的低维表示,具有单位协方差,并最小化相同的重建误差:
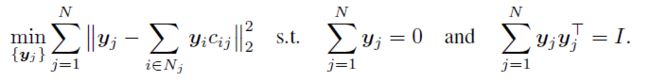
LLE VS Local-attention
为证明LLE使用了mask的Local-attention机制, x j ≈ ∑ i ∈ N j x j c i j x_j≈\sum_{i\in N_j}x_jc_{ij} xj≈∑i∈Njxjcij可以被解释为测量属于K近邻的 x i x_i xi到点 x j x_j xj的贡献的注意力权重。请注意,对每个 x j x_j xj的重构损失的优化问题可以解耦为N个优化问题,并且最优系数 c i j ∗ c^*_{ij} cij∗是对query x j x_j xj和keys { x i } i ∈ N j \{x_i\}_{i\in N_j} {xi}i∈Nj的函数,即:
![]()
由于不属于K近邻的其它系数 { c i j ∗ } i ∉ N j \{c^*_{ij}\}_{i\notin N_j} {cij∗}i∈/Nj被设置为0,因此这些K近邻点定义了Local-attention的mask:用局部的K近邻去预测被mask掉的token x j x_j xj。还要注意,由于约束已经确保权重累和为1,因此不需要softmax后处理。
尽管LLE和现有的注意机制有这些相似之处,但也有一些重要的区别:
- 大多数现有的attention机制计算用于单个Query-Key点对的得分函数,然后应用softmax函数,以便使权重介于0和1之间。相比之下,LLE系数取决于单个Query(被mask的 x j x_j xj)和多个Key(K近邻点集 { x i } i ∈ N j \{x_i\}_{i\in N_j} {xi}i∈Nj),且LLE的系数不受非负约束。
- 另一个区别,也许是最重要的区别,是在大多数现有的attention机制中, c i j c_{ij} cij是Query-Key点对的参数化函数,其权重是在训练期间学习。而LLE直接学习 c i j c_{ij} cij的值,这使得这些系数难以用于评估新数据,优化问题需要重新求解。
尽管存在这些差异,我们注意到许多关键的注意力成分(KQV、mask)已经存在于最初的LLE公式中(尽管出于不同的目的)。特别地,LLE基于这样一种思想:即每个Query通过将自己表出为很可能是同一类的K-近邻的仿射组合。因此,注意力权重捕获数据流形的局部几何结构,并据此用于 y j y_j yj找到低维嵌入。
5 Subspace clustering, Self-expression and Self-attention
LLE的一个关键限制是它的局部邻域是预先指定的,因此数据点不能关注任何其他点。在本节中,self-expression解了决这个问题,它将每个点连接到每个其他点,并使用稀疏正则化来揭示需要关注的点。具体的,如稀疏子空间聚类、低秩子空间聚类、最小二乘回归及其扩展使用mask的全局自注意力机制计算数据之间的关联,其中Query、Key和Value都是待聚类的数据点。我们还表明,自表达系数是全局的,因为它们真正依赖于多个数据点,不像大多数注意力机制只依赖于一对token。最后,我们证明了子空间聚类训练目标可以解释为一个填补空白的自监督学习目标,其中每个数据点相对于所有其他数据点进行回归。
5.1 Subspace clustering and Self-expression
子空间聚类是指对从子空间的并集中提取的数据进行聚类的问题。基于自表达的方法通过将每个数据点表示为所有其他数据点的线性组合来解决此问题。由此产生的自表达系数揭示了关于哪些点属于同一子空间的信息,因此它们可用于定义合适的数据关联矩阵。然后,通过将谱聚类应用于该Affinity来获得聚类结果:
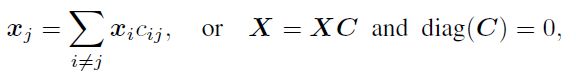
理想情况下,系数应具有子空间保持特性(非零 c i j c_{ij} cij对应的 x i x_i xi均来自和 x j x_j xj同一个子空间)。满足这种性质的 c i j c_{ij} cij是一定存在的,因为一个点总是可以用它自己的子空间中其它的点来表示。此外,如果 d < < N d<
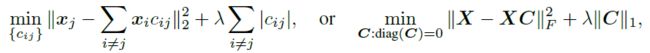
一旦得到了系数矩阵,通常只选择最大的那些非零系数(丢弃接近于0的系数),以产生额外的稀疏性,并对C的列进行归一化,使它们累和为1。有趣的是,似乎在子空间聚类文献中从未对系数使用过sofmax进行归一化。最后,通过将谱聚类应用于Affinity矩阵对数据进行聚类,通常通过对称化自表达系数的绝对值来构造 A = ∣ C ∣ + ∣ C ⊤ ∣ A=| C |+| C^\top| A=∣C∣+∣C⊤∣。
5.2 使用不同正则化的自表达系数
LSR使用 ∥ C ∥ F 2 \|C\|^2_F ∥C∥F2并给出了C的闭式解: C = ( X ⊤ X + λ I ) − 1 X ⊤ X = V ( Σ 2 + λ I ) − 1 Σ 2 V ⊤ \bf C=(X^\top X+\lambda I)^{-1}X^\top X=V(\Sigma^2+\lambda I)^{-1}\Sigma ^2V^\top C=(X⊤X+λI)−1X⊤X=V(Σ2+λI)−1Σ2V⊤,其中X可以被SVD分解: X = U Σ V ⊤ \bf X=U\Sigma V^\top X=UΣV⊤。因此,自表达系数 c i j = v i ⊤ ( Σ 2 + λ I ) − 1 Σ 2 V ⊤ c_{ij}=\bf v_i^\top(\Sigma ^2+\lambda I)^{-1}\Sigma ^2V^\top cij=vi⊤(Σ2+λI)−1Σ2V⊤是对 V \bf V V的行进行加权点积。当 λ \lambda λ足够大时我们就得到了对数据 X X X的缩放点积:
C = ( X ⊤ X + λ I ) − 1 X ⊤ X ≈ ( λ I ) − 1 X ⊤ X = 1 λ X ⊤ X C=(X^\top X+\lambda I)^{-1}X^\top X≈(\lambda I)^{-1}X^\top X=\frac{1}{\lambda}X^\top X C=(X⊤X+λI)−1X⊤X≈(λI)−1X⊤X=λ1X⊤X
低秩子空间聚类方法使用核范数正则化 ∥ C ∥ ∗ \|C\|_∗ ∥C∥∗诱导低秩系数。数据的奇异值分解(SVD)的闭式解可计算为 C = V R e L U λ ( Σ ) V ⊤ C=\textbf V ReLU_λ(\Sigma)\textbf V^\top C=VReLUλ(Σ)V⊤ 其中 R e L U λ ( x ) = m a x ( x − λ , 0 ) ReLU_λ(x)=max(x−λ,0) ReLUλ(x)=max(x−λ,0),如前一样,这可以解释为对V的行的加权点积,除了一些权重可以为零以诱导低秩。
稀疏子空间聚类方法使用 ℓ 1 \ell_1 ℓ1范数 ∥ C ∥ 1 \|C\|_1 ∥C∥1来诱导稀疏系数。在这种情况下不能以闭合形式计算系数。然而,一种常见的方法是使用(Beck&Teboulle,2009)提出的迭代收缩阈值算法(Iterative Shrinkage Thresholding Algorithm, ISTA),C的迭代可以写成:
![]()
其中 ϵ > 0 \epsilon >0 ϵ>0为步长。我们注意到,上式是(Gregor&LeCun,2010)中提出的展开方法的出发点,该方法将稀疏编码与神经网络连联系起来。在该方法中,迭代被解释为神经网络的激活函数和对 C C C的线性变换 ( I − ϵ X ⊤ X ) (I−\epsilon X^\top X) (I−ϵX⊤X) 和可学习权重 X ⊤ X X^\top X X⊤X。
作为未来的研究方向,我们建议进一步探索稀疏子空间聚类和Transformer的联系,我们推测这将允许我们通过使用(深层)多层的注意力模型将子空间聚类扩展到非线性流形。更具体地说,我们可以部分地将ISTA重新解释为单个注意力层的更新。这是因为在上述等式中, X − X C k X− XC_k X−XCk项可以解释为对输入数据 X X X应用注意力 C k C_k Ck,然后添加一个(负的)残差链接 X X X,再然后乘以 X ⊤ X^\top X⊤。ReLU的非线性可以解释为Transformer的前馈层。当然,这个类比并不完美,因为添加 C k C_k Ck并不完全是一个残差链接。
这可能会成为一个稀疏的transformer?
5.3 Self-expressiveness VS Self-attention
自表达可以被解释为一种Self-attention机制,其中Query q j = x j q_j=x_j qj=xj被表示为所有Value v i = x i v_i=x_i vi=xi的线性组合,注意力系数 c i j c_{ij} cijQuery q j = x j q_j=x_j qj=xj和Key v i = x i v_i=x_i vi=xi确定。然而,我们注意到,自表达系数(SEC)比自注意力系数更具有一般性:
- SEC无非负性约束,允许正、负注意力。
- SEC不限于单个 key-query对的显式函数。例如,最小二乘回归的闭式解具有 ( λ I + X ⊤ X ) − 1 (λI+X^\top X)^{-1} (λI+X⊤X)−1形式的项,使 c i j c_{ij} cij成为所有key-query对的函数。自表达系数为单个 key-query对的显式函数的唯一情况是 λ λ λ足够大时,如前所述,此时类似于缩放点积。
- SEC使用无监督损失直接学习系数。然而,这是自表达的一个潜在缺点,因为它使在测试时计算系数变得困难。该问题在(张尚之等人的SENet)中通过使用可学习的系数解决。
- SEC通常被正则化为稀疏或低秩。我们认为,使用稀疏正则化来自动选择最相关的系数,是处理大量token时的一种更为原则性的方法,而不是任意地将注意力限制在局部近邻。
因此,我们认为,相比于自表达模型,self-attention的关键创新不在于其捕捉适应数据的全局联系的能力(因为self-expression已经做到了这一点),而是在于注意力机制并行地使用多个注意力头,并堆叠到深层架构中。如前一节所述,通过进一步探索稀疏子空间聚类和Transformer之间的联系可能会得到(深层)多层子空间聚类模型;或者使用注意机制来参数化自表达系数,如SENet做的那样。
6 结论
我们已经证明,注意力建立在流形学习和图像处理的长期历史上,包括基于核的回归、非局部均值、局部线性嵌入、子空间聚类和稀疏编码等方法。特别是,我们表明,注意力背后的许多关键思想,例如它捕捉全局远程交互的能力(这些互动是可学习的和适应输入的),已经出现在其它文献中。因此,与现有技术相比,注意力机制的关键创新在于使用许多可学习的参数以及多个头部和层次。



